Was ist eine einfaktorielle ANOVA?
Die einfaktorielle ANOVA (Varianzanalyse) ist ein statistischer Test, der verwendet wird, um zu prüfen, ob es signifikante Unterschiede zwischen den Mittelwerten von zwei oder mehr Gruppen gibt. Es wird angenommen, dass die Gruppen normalverteilt und unabhängig voneinander sind und dass die Varianzen der Gruppen ähnlich sind. Diese Anleitung zeigt, wie du die einfaktorielle ANOVA in SPSS berechnest.
Wenn wir die Mittelwerte von Gruppen betrachten, sehen wir oft Unterschiede. Die durchschnittlichen Mietpreise von Städten wie München, Berlin oder Frankfurt unterscheiden sich. Und obwohl wir einen Unterschied in den durchschnittlichen Mietpreisen messen können, wissen wir nicht, ob dieser Unterschied signifikant ist. Wir müssen also herausfinden, ob die Unterschiede zwischen den Mittelwerten so groß sind, dass wir ausschließen können, dass es sich um rein zufällige Unterschiede handelt. Deshalb untersuchen wir die Mittelwertunterschiede mit einer Varianzanalyse und testen, wie hoch ihr Signifikanzniveausignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist. (bzw. ihre Effektstärke) ist.
Betrachtet man die Mittelwerte der Gruppen, so zeigen sich häufig Unterschiede. Die durchschnittlichen Mietpreise in Städten wie München, Berlin oder Frankfurt unterscheiden sich. Und obwohl wir einen Unterschied in den durchschnittlichen Mietpreisen messen können, wissen wir nicht, ob dieser Unterschied signifikant ist. Wir müssen also herausfinden, ob die Unterschiede zwischen den Mittelwerten so groß sind, dass wir ausschließen können, dass es sich um rein zufällige Unterschiede handelt. Deshalb untersuchen wir die Mittelwertunterschiede mit einer Varianzanalyse und testen, wie hoch das Signifikanzniveau (oder die Effektstärke) ist.
In dieser Anleitung zur einfaktoriellen ANOVA in SPSS berechnen wir ein Beispiel mit verschiedenen Immobilienpreisen und überlegen, wie wir unsere Forschungsfragen am besten beantworten können.
Was berechnen wir bei der ANOVA?
Die einfaktorielle ANOVA wird verwendet, wenn es nur eine unabhängige Variable gibt, die die zu untersuchenden Gruppen unterscheidet. Die ANOVA berechnet den F-Wert, der angibt, ob es signifikante Unterschiede zwischen den Gruppen gibt. Ist der F-Wert signifikant, bedeutet dies, dass es wahrscheinlich Unterschiede zwischen den Gruppen gibt. Ist der F-Wert nicht signifikant, bedeutet dies, dass es keine Unterschiede zwischen den Gruppen gibt.
Der Versuchsaufbau, bei dem die Mittelwerte der abhängigen Variablen zwischen mehreren Gruppen verglichen werden, wird als Between-Subjects-Design bezeichnet. Die ANOVA selbst liefert uns nur einen p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist., der statistisch signifikant sein kann – oder auch nicht. Signifikanz bedeutet, dass sich der Mittelwert mindestens einer Gruppe nicht nur zufällig von den Mittelwerten der anderen Gruppen unterscheidet. Welche Gruppe(n) das genau sind, kann nur durch weitere Tests, so genannte Post-hocPost Hoc Post-hoc-Analysen sind Analysen, die nach der Durchführung einer Studie durchgeführt werden, um die Ergebnisse der Studie zu interpretieren und zu vertiefen.-Analysen, festgestellt werden. Eine Schritt-für-Schritt-Anleitung finden Sie in den folgenden Tutorials.

Wann verwendet man eine einfaktorielle ANOVA in SPSS?
Die einfaktorielle ANOVA (Varianzanalyse) wird verwendet, um zu prüfen, ob es signifikante Unterschiede zwischen den Mittelwerten von zwei oder mehr unabhängigen Gruppen gibt. Es wird angenommen, dass die Gruppen normalverteilt und unabhängig sind und dass die Varianzen der Gruppen ähnlich sind.
Die einfaktorielle ANOVA wird verwendet, wenn es nur eine unabhängige Variable gibt, die die zu untersuchenden Gruppen unterscheidet. Wenn es mehrere unabhängige Variablen gibt, die die Gruppen unterscheiden, wird eine multifaktorielle ANOVA verwendet. Eine unabhängige Variable könnte “Stadt” mit den Ausprägungen “München”, “Frankfurt”, “Berlin” sein.
Weitere Beispiele für Fragestellungen, die mit Hilfe der einfaktoriellen ANOVA untersucht werden können, sind
- Gibt es signifikante Unterschiede zwischen den durchschnittlichen Bearbeitungszeiten der Schülerinnen und Schüler verschiedener Schulen?
- Gibt es signifikante Unterschiede zwischen den durchschnittlichen Gewichten von Tieren, die verschiedenen Fütterungsregimen ausgesetzt waren?
- Gibt es signifikante Unterschiede zwischen den durchschnittlichen Verkaufszahlen von Produkten, die in verschiedenen Verpackungen verkauft wurden?
Voraussetzungen
- Unabhängige Messungenunabhängige Messungen Unabhängige Messungen sind Messungen, die von verschiedenen Beobachtern oder Messverfahren durchgeführt werden und die vermutlich keine Wechselwirkungen oder Verzerrungen durch die Beobachter oder Messverfahren haben. Sie werden verwendet, um die Zuverlässigkeit und Validität von Messungen und Studien zu verbessern und werden häufig in der Psychologie und Sozialwissenschaften verwendet.: die Varianzanalyse vergleicht unterschiedliche Messobjekte, in unserem Fall Versuchspersonen, zu unterschiedlichen Zeitpunkten. Die Gruppen oder Bedingungen (UV) dürfen sich nicht gegenseitig beeinflussen, dass heißt eine Versuchsperson darf sich unter keinen Umständen in mehreren Gruppen zu befinden.
- SkalenniveausSkalenniveau Das Skalenniveau bezieht sich auf den Typ von Daten, der in einer Studie erhoben wurde, und gibt an, wie die Daten in Bezug auf die Messbarkeit und die Möglichkeit zur Verwendung von Statistiken kodifiziert sind.: die unabhängige Variable (Zeitpunkt der Messung) ist nominalskaliert, während die abhängige Variableabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. (Gewicht) mindestens intervallskaliert ist. Mehr Informationen über Skalenniveaus.
- AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind.: Die ANOVA ist empfindlich gegenüber Ausreißern, weshalb der Datensatz auf Ausreißer hin überprüft werden sollte. Anleitung Ausreißer finden.
- NormalverteilungNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. : die abhängige Variable (Gewicht) in jeder Gruppe sollte so weit wie möglich normalverteilt sein – jedoch nicht zwangsläufig. Die Berechnung in SPSS wird später Schritt für Schritt erklärt. Normalverteilung prüfen.
- HomoskedastizitätHomoskedastizität Homoskedastizität bezieht sich auf die Gleichmäßigkeit der Varianz der Residuen in einem statistischen Modell und bedeutet, dass die Varianz der Residuen über alle Werte der unabhängigen Variablen hinweg konstant ist. Eine Homoskedastizität wird als Vorbedingung für viele statistische Tests und Schätzverfahren angesehen und kann durch eine Gleichmäßigkeit der Streuung der Datenpunkte um die Regressionslinie in einem Scatterplot dargestellt werden.: die Varianzen aller Gruppen sollte ungefähr gleich groß sein, um zu vermeiden eine Nullhypothese zurückzuweisen, die eigentlich war ist. Die Berechnung der Homoskedastizität wird später Schritt für Schritt erklärt. Anleitung für Homoskedastizität.
Einfaktorielle ANOVA in SPSS berechnen
Schritt für Schritt die einfaktorielle ANOVA in SPSS einstellen und die richtigen Analysemethoden wählen
Einfaktorielle Varianzanalyse (ANOVA) auswählen

Die einfaktorielle ANOVA wird in SPSS gestartet. Navigieren Sie dazu zu Analysieren > Mittelwerte vergleichen > Einfaktorielle Varianzanalyse (ANOVA
Dialogbox einfaktorielle Varianzanalyse

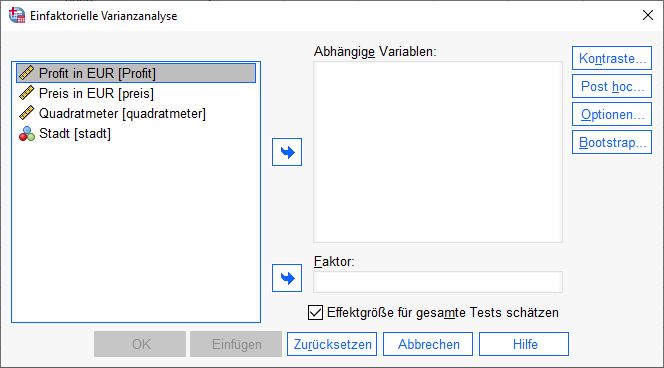
SPSS öffnet das Dialogfenster “einfaktorielle Varianzanalyse (ANOVA)”. Dieses Fenster ist zweigeteilt. Auf der linken Seite befinden sich die verfügbaren Variablen aus dem Datensatz. Auf der rechten Seite befindet sich das Feld “Abhängige Variablenabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. ”.
In dieses Feld werden die Variablen eingetragen, die in die Berechnung einbezogen werden sollen.
Wir markieren eine Variable auf der linken Seite und klicken auf den kleinen blauen Pfeil zwischen den beiden Feldern. Ein Klick auf den Pfeil verschiebt die markierte Variable von links nach rechts. Alternativ klicken wir mit der linken Maustaste auf eine Variable auf der linken Seite und halten die Maustaste gedrückt. Bei gedrückter Maustaste wird die Variable nach links verschoben. Dieser Vorgang wird “Drag and Drop” genannt.Hinweise:
Es ist möglich, mehrere abhängige Variablen für die Analyse auszuwählen.
Beachten Sie, dass Faktor die abhängige Variable ist (Zwischensubjektfaktor).
Um eine Variable in das Feld “Faktor” zu ziehen, gehen Sie genauso vor wie bei den abhängigen Variablen.Variablen der Varianzanalyse in SPSS zuordnen

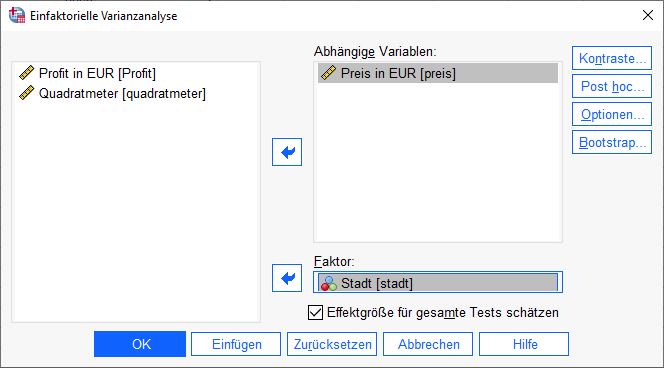
Für unser Beispiel verwenden wir die Variable “Preis in EUR” als abhängige Variable und die Variable “Stadt” als Faktor.
Hinweis: Mit dieser Einstellung unterscheiden wir die Städte mit ihren Ausprägungen von “Gewinn”.
Wir wählen die Schaltfläche “Optionen” für die Varianzanalyse aus

Auf der rechten Seite befindet sich ein Menü mit mehreren Auswahlmöglichkeiten. Wir wählen “Optionen” und klicken darauf.
Einstellung der Optionen der einfaktoriellen ANOVA in SPSS

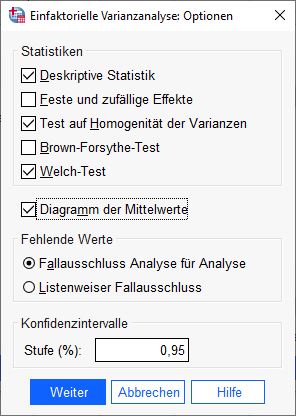
Ein Dialogfenster öffnet sich. Hier wählen wir folgende Optionen: “Deskriptive Statistik”, “Test auf Homogenität der Varianzen”, “Welch-Test”, “Mittelwertgrafik” und “Fallzusammenfassung Analyse für Analyse”.
Klicken Sie auf Weiter, um die Eingaben zu bestätigen.
Hinweis: Die ausgewählten Analysen werden später benötigt.
Post HocPost Hoc Post-hoc-Analysen sind Analysen, die nach der Durchführung einer Studie durchgeführt werden, um die Ergebnisse der Studie zu interpretieren und zu vertiefen. Test für die einfaktorielle ANOVA in SPSS auswählen

Wir befinden uns wieder im ersten Menü. Auf der rechten Seite wählen wir “Post hoc”.
Auswahl der Post Hoc Tests der Varianzanalyse (ANOVA)

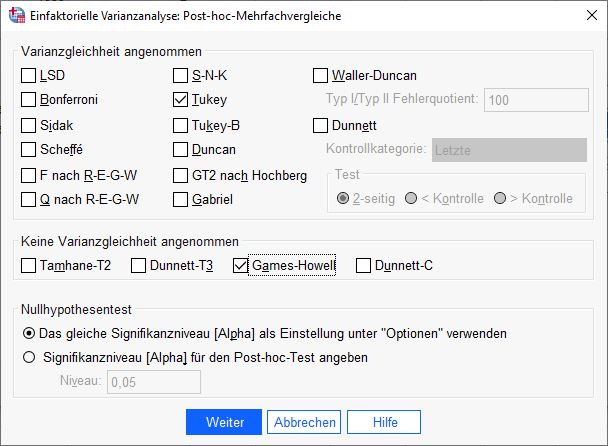
Es öffnet sich ein Dialogfenster mit mehreren Alternativen für die Post-Hoc-Berechnung. Alle Verfahren haben Vor- und Nachteile. In diesem Handbuch werden Tukey und Games-Howell verwendet. Damit haben wir bewährte Verfahren für angenommene und nicht angenommene Varianzgleichheit.
Klicken Sie auf Weiter, um die Eingaben zu bestätigen.
Hinweis: Wenn wir bei der späteren Analyse der Homoskedastizität feststellen, dass diese Bedingung verletzt ist, haben wir die entsprechenden Berechnungen sofort zur Hand.
Kurze Erläuterung der Analysen:
Bei den Testverfahren unterscheiden wir zwischen konservativen (strengen) und liberalen Verfahren. Duncan und Scheffé gelten als konservativ, SNK und LSD als liberal. Der Tukey-Test ist in dieser Hinsicht ein guter Allrounder. Alternativ kann Bonferroni verwendet werden. Weitere Vor- und Nachteile ergeben sich aus Kriterien wie der Stichprobengröße. Bei sehr kleinen Stichproben kann ein Dunnett-Test empfohlen werden.Berechnung der Varianzanalyse in SPSS starten

Wir sind wieder bei der ersten Ansicht. Die Einstellungen passen. Wir sind bereit für die Berechnung. Wir klicken auf OK.
Interpretation der Ergebnisse
Deskriptive Analysen
SPSS öffnet im Ausgabefenster mehrere Tabellen zu wichtigen Statistiken wie Mittelwerte, Standardfehler oder VarianzhomogenitätVarianzhomogenität Varianzhomogenität bezieht sich auf die Gleichmäßigkeit der Varianzen zwischen zwei oder mehr Gruppen und ist eine Vorbedingung für viele statistische Tests, die die Gleichheit der Gruppen untersuchen. Eine Varianzhomogenität wird angenommen, wenn die Varianzen der Gruppen ähnlich sind und bedeutet, dass keine Gruppe signifikant von den anderen Gruppen abweicht. Eine nicht vorhandene Varianzhomogenität kann dazu führen, dass die Ergebnisse von Tests verzerrt werden und kann darauf hinweisen, dass es in den Gruppen Unterschiede gibt, die berücksichtigt werden müssen., die wir nacheinander besprechen. Beginnen wir mit den deskriptiven Statistiken. Jede Ausprägung des Faktors wird in der Übersicht mit diesen Kennzahlen dargestellt: Anzahl (N), arithmetisches Mittel (Mean), StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. (Std. DeviationStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. ), Standardfehler (Std. Error), Untergrenze (Lower Bound), Obergrenze (Upper Bound) des Konfidenzintervalls sowie Minima und Maxima.
In unserem Beispiel sehen wir, dass die meisten untersuchten Fälle aus Frankfurt stammen (N=61) und der durchschnittliche Gewinn m=177.265,57 (sd=120.228,61) beträgt. Den geringsten durchschnittlichen Gewinn erzielen die Restaurants in Berlin (m=110.583,33, sd=80.515,21).
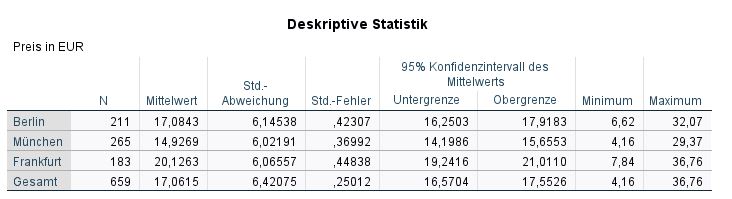
Weiter unten in der SPSS-Ausgabe befindet sich ein Diagramm, das die Mittelwerte dieser Tabelle visualisiert.
Überprüfung der Varianzhomogenität als Voraussetzung
Zunächst werden einige Voraussetzungen für eine einfaktorielle ANOVA geprüft. Schließlich wird geprüft, ob die Varianz des Faktors in den untersuchten Gruppen gleich ist. Dazu werden die Ergebnisse des Levene-Tests betrachtet. Die Varianzhomogenität sollte gegeben sein, daher wird der Signifikanzwert geprüft, der über p=.05 liegen sollte. Dies bedeutet, dass ein signifikantes Ergebnis (p<.05) die Varianzhomogenität verletzt.
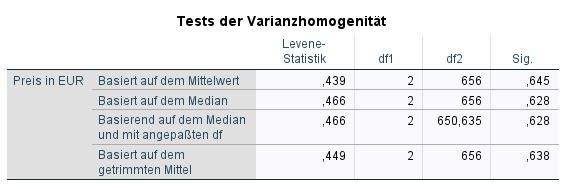
In unserem Beispiel ist die Varianzhomogenität nicht gegeben, da der Levene-Test mit p=.003 ein signifikantes Ergebnis zeigt (p<0.5). In diesem Handbuch werden alle Varianten erläutert.
Weiteres Vorgehen
Wenn die Varianzhomogenität gegeben ist, dann verwenden wir zu einem späteren Zeitpunkt den Post Hoc Test: Tukey Test.
Wenn die Varianzhomogenität nicht gegeben ist, dann verwenden wir die Welch ANOVA und den Post Hoc Test: Games-Howel.
Interpretation der Analysis of Variance (ANOVA)
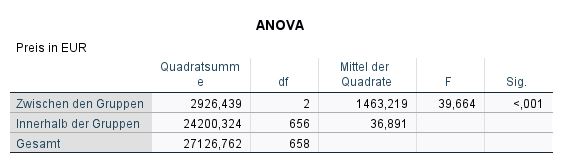
Wenn alle Voraussetzungen und die Varianzhomogenität in deinem Datensatz erfüllt sind, kannst du dir die Tabelle „Einfaktorielle ANOVA“ (ANOVA) ansehen. Die wichtigste Kennzahl ist das Signifikanzniveau in der Spalte Sign. Es gibt an, ob die Mittelwertunterschiede zwischen den Gruppen zufällig sind oder nicht. Liegt die gemessene Signifikanz bei 5% oder darunter (p<0,5), sprechen wir von einem signifikanten Ergebnis. Alle anderen Werte weisen auf nicht signifikante Ergebnisse hin.
In unserem Fall kann eine Signifikanz (zwischen den Gruppen) von p=.002 gemessen werden. Dies bedeutet, dass sich mindestens zwei Gruppen in diesem Faktor signifikant unterscheiden.
Ergebnisse publizieren
Der ökonomische Erfolg, gemessen anhand der Variable “Gewinn”, unterschied sich statistisch signifikant für die verschiedenen Städte der Untersuchung, F(2, 147) = 6.78, p < .01.
Die ANOVA-Schreibweise richtig verwenden
Die ANOVA wird wie folgt dargestellt:
F(dfZähler, dfNenner) = F-Wert, p = Signifikanz
Die Daten für die Formel befinden sich in der ANOVA-Tabelle. Die erste Zeile in der Spalte df (Freiheitsgrade) zeigt den Wert 2. Der F-Wert steht in der vorletzten Spalte (F), die Signifikanz in der letzten Spalte.
- F: Der F-Wert sagt aus, dass eine F-Statistik benutzt wurde.
- (2,147): Die Grenzen der F-Verteilung werden von diesen zwei Parametern bestimmt.
- 6.78: Der sogenannte F-Wert gibt den Wert an, der in der F-Verteilung zur Bestimmung des p-Wertes nachgeschlagen wird.
- .000: Der p-Wert sagt aus, ob ein Ergebnis signifikant ist oder nicht.
Anmerkung: Theoretisch kann die Signifikanz nie .000 erreichen, auch wenn SPSS diesen Wert ausgibt. In diesem Fall geben wir den gerundeten Wert p<.001 an. Da unsere Beispieldaten keine Varianzhomogenität aufweisen, betrachten wir weiter unten die Ergebnisse der Welch ANOVA. Die Welch ANOVA ist etwas „robuster“ gegenüber Verletzungen der Varianzhomogenität. In unserem Beispiel erhalten wir immer noch ein hochsignifikantes Ergebnis (p=.003).
Berechnung mit der Welch-Anova

Wir testen unsere Ergebnisse mit der Welch-ANOVA. Die Unterschiede zwischen den Gruppen sind insgesamt signifikant.
Weiteres Vorgehen
Wenn das Ergebnis der ANOVA-Berechnung signifikant ist, wird im nächsten Schritt eine Post-hoc-Analyse durchgeführt, um zu verstehen, welche Gruppen sich im Detail signifikant unterscheiden.
Post Hoc Tests
Die Post-Hoc-Analyse ist eine detailliertere Betrachtung der einzelnen Unterschiede in der ANOVA. Wir verwenden die Post-Hoc-Analyse, weil die vorangegangene Berechnung ein sogenanntes Omnibusverfahren ist. Wir wissen nur, dass sich die Gruppen signifikant unterscheiden, ohne zu wissen, zwischen welchen Gruppen es signifikante Unterschiede gibt.
In der Tabelle sehen wir zwei große Bereiche: Tukey HSD und Games-Howell. Wenn Varianzhomogenität gegeben ist, interpretieren wir den Tukey HSD-Test. Wenn die Varianzhomogenität nicht gegeben ist, betrachten wir die Analysen des Games-Howell Post Hoc Tests.
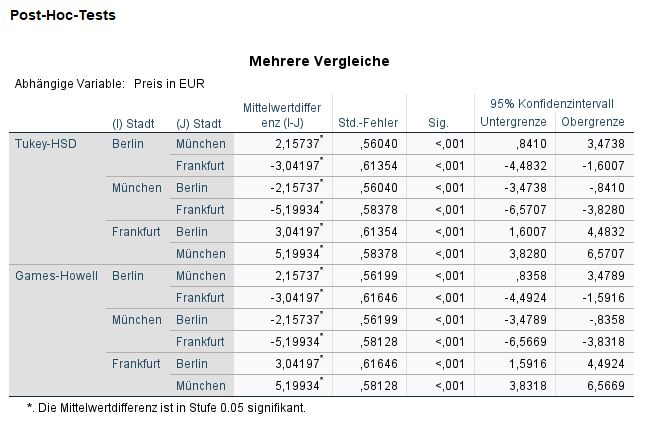
Beginnen wir mit der Analyse. In unserem Beispiel ist die Varianzhomogenität nicht gegeben (siehe oben), daher betrachten wir die Ergebnisse in den Zeilen “Games-Howell”. Wenn wir uns die Ergebnisse in der Spalte “Mittelwertsunterschiede” genauer ansehen, stellen wir fest, dass die Ergebnisse zweimal mit unterschiedlichen Vorzeichen erscheinen. Dies liegt daran, dass SPSS die Analyse in beide Richtungen durchführt. SPSS vergleicht die drei Gruppen Berlin-Frankfurt (p=0.02), Berlin-München (p=0.79) und Frankfurt-München (p=.029) mit den jeweiligen Mittelwertsdifferenzen (Mean Difference) und Standardabweichungen (Std. Error).
Ergebnisse publizieren
Der Tukey post-hoc Test zeigte einen signifikanten Unterschied (p < .002) der abhängigen Variable Gewinn zwischen den Gruppen Berlin-Frankurt (p=.002) und Frankfurt-München (p=.029). Es konnte keine signifikanten Unterschiede zwischen den Gruppen Berlin-München (p=0.79) festgestellt werden.
Anmerkung: In einigen Fällen zeigt die einfaktorielle ANOVA ein signifikantes Ergebnis, während gleichzeitig die Post-hoc-Tests keine Signifikanz zwischen den Gruppen nachweisen können und umgekehrt. Häufig liegt dies an der unterschiedlichen Berechnung (PowerStatistische Power Statistische Power ist die Wahrscheinlichkeit, dass ein statistisches Testverfahren einen wirklich vorhandenen Unterschied zwischen zwei Gruppen oder Bedingungen erkennen wird. Eine hohe statistische Power bedeutet, dass das Testverfahren empfindlich genug ist, um kleine Unterschiede zu erkennen, während eine niedrige statistische Power dazu führen kann, dass wichtige Unterschiede übersehen werden. Es ist wichtig, dass die statistische Power bei der Planung einer Studie berücksichtigt wird, um sicherzustellen, dass das Testverfahren ausreichend empfindlich ist, um wichtige Unterschiede zu erkennen. ) der verwendeten Tests.
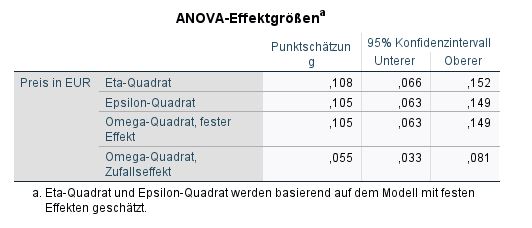
Effektstärken berechnen
Häufig gestellte Fragen und Antworten zu einfaktorielle ANOVA in SPSS
Was zeigt eine ANOVA?
ANOVA (Analysis of Variance) ist ein statistisches Verfahren, das verwendet wird, um zu prüfen, ob es signifikante Unterschiede zwischen den Mittelwerten von zwei oder mehr Gruppen gibt. Sie wird häufig verwendet, um zu prüfen, ob es Unterschiede zwischen den Mittelwerten verschiedener Behandlungsgruppen oder zwischen verschiedenen Untergruppen innerhalb einer Behandlungsgruppe gibt.
Die ANOVA wird auf der Grundlage von Stichproben aus den verschiedenen Gruppen berechnet und gibt eine Vorhersage darüber, wie wahrscheinlich es ist, dass die beobachteten Unterschiede zwischen den Mittelwerten der Gruppen auf Zufall zurückzuführen sind. Wenn die Wahrscheinlichkeit, dass die Unterschiede auf Zufall zurückzuführen sind, sehr gering ist (in der Regel wird ein Signifikanzniveau von 0,05 oder weniger verwendet), kann davon ausgegangen werden, dass tatsächlich signifikante Unterschiede zwischen den Mittelwerten der Gruppen bestehen.
Die ANOVA kann auch verwendet werden, um zu prüfen, ob es Unterschiede zwischen den Mittelwerten von mehr als zwei Gruppen gibt, indem sogenannte “multiple Vergleiche” durchgeführt werden. Diese Vergleiche können verwendet werden, um zu prüfen, ob es signifikante Unterschiede zwischen den Mittelwerten bestimmter Gruppen gibt, während die Unterschiede zwischen den anderen Gruppen vernachlässigt werden.
Was sagt die Varianzanalyse aus?
Varianzanalyse ist ein anderes Wort für ANOVA (Analysis of Variance). Die Varianzanalyse ist besonders nützlich, wenn der Einfluss verschiedener Faktoren auf eine abhängige Variable untersucht werden soll. Beispielsweise kann die Wirkung verschiedener Marketingkampagnen auf den Absatz eines Produkts untersucht werden, wobei der Absatz als abhängige Variable und die Marketingkampagnen als unabhängige Variablen betrachtet werden. Die Varianzanalyse kann dann verwendet werden, um zu prüfen, ob es signifikante Unterschiede zwischen den Mittelwerten der Verkaufszahlen der verschiedenen Marketingkampagnen gibt.
Wann wendet man ANOVA noch an?
ANOVA (Analysis of Variance) ist eine statistische Methode, die häufig verwendet wird, um zu prüfen, ob es signifikante Unterschiede zwischen den Mittelwerten von zwei oder mehr Gruppen gibt. Je nach Art der Variablen und der Anzahl der zu untersuchenden Gruppen gibt es verschiedene Arten der ANOVA.
Neben der einfaktoriellen ANOVA, die verwendet wird, wenn es nur eine unabhängige Variable gibt, in der sich die Gruppen unterscheiden, gibt es auch die multifaktorielle ANOVA.
– Multifaktorielle ANOVA: Sie wird verwendet, wenn es mehrere unabhängige Variablen gibt, die die Gruppen unterscheiden.
– ANOVA mit wiederholten Messungen: Wird verwendet, wenn dieselben Teilnehmer in mehreren Gruppen untersucht werden.
Mixed ANOVA: Wird verwendet, wenn einige Teilnehmer mehrfach und andere nur einmal gemessen werden.
Die ANOVA wird häufig in der Psychologie, den Sozialwissenschaften, der Biologie und anderen Bereichen verwendet, in denen geprüft werden soll, ob es signifikante Unterschiede zwischen den Mittelwerten von Gruppen gibt. Beispiele für Fragen, die mit Hilfe der ANOVA untersucht werden können, sind folgende:
– Gibt es signifikante Unterschiede zwischen den Durchschnittsnoten von Studierenden, die unterschiedlichen Lehrmethoden ausgesetzt waren?
– Gibt es signifikante Unterschiede zwischen den Durchschnittsgewichten von Tieren, die verschiedenen Fütterungsregimen ausgesetzt waren?
– Gibt es signifikante Unterschiede zwischen den durchschnittlichen Verkaufszahlen von Produkten, die in verschiedenen Ländern verkauft werden?
Wann ANOVA und wann t-Test?
ANOVA (Analysis of Variance) und t-Test sind zwei statistische Verfahren, die verwendet werden, um zu prüfen, ob es signifikante Unterschiede zwischen den Mittelwerten von zwei oder mehr Gruppen gibt. Der t-Test eignet sich jedoch für den Vergleich von genau zwei Gruppen, während die ANOVA für den Vergleich von mehr als zwei Gruppen geeignet ist.
Wenn Sie also genau zwei Gruppen vergleichen wollen, z. B. die Leistungen von Schülern in zwei verschiedenen Klassen, werden Sie in der Regel den t-Test verwenden. Wenn Sie dagegen mehr als zwei Gruppen vergleichen wollen, z. B. die Leistungen von Schülern in drei verschiedenen Schulen, werden Sie normalerweise die ANOVA verwenden.
Es gibt jedoch Fälle, in denen die ANOVA und der t-Test kombiniert werden können.
Zum Beispiel könnte man die ANOVA verwenden, um zu prüfen, ob es signifikante Unterschiede zwischen den Mittelwerten mehrerer Gruppen gibt, und dann den t-Test verwenden, um zwischen den Gruppen zu unterscheiden, in denen es tatsächlich signifikante Unterschiede gibt.
Welche ANOVAS gibt es?
Einfaktorielle ANOVA: Diese Art der ANOVA wird verwendet, wenn die Wirkung eines einzelnen Faktors auf eine abhängige Variable untersucht werden soll. Beispielsweise könnte die Wirkung verschiedener Marketingkampagnen auf den Absatz eines Produkts untersucht werden, wobei der Absatz als abhängige Variable und die Marketingkampagnen als unabhängige Variablen betrachtet werden.
– Multifaktorielle ANOVA: Diese Art der ANOVA wird verwendet, wenn der Einfluss mehrerer Faktoren auf eine abhängige Variable untersucht werden soll. Beispielsweise könnte der Einfluss von Alter, Geschlecht und Bildungsniveau auf die Meinung einer Person zu einem bestimmten Thema untersucht werden.
– Unabhängige Stichproben ANOVA: Diese Art der ANOVA wird verwendet, wenn Mittelwerte zwischen zwei oder mehr Gruppen verglichen werden sollen, die völlig unabhängig voneinander sind. Zum Beispiel könnte man die Durchschnittsgehälter von Männern und Frauen in verschiedenen Unternehmen vergleichen.
– Abhängige Stichproben ANOVA: Diese Art der ANOVA wird verwendet, wenn Mittelwerte zwischen zwei oder mehr Gruppen verglichen werden sollen, die miteinander verbunden sind, z.B. wenn dieselben Personen zu verschiedenen Zeitpunkten oder unter verschiedenen Bedingungen gemessen werden.
Es gibt noch weitere Formen.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn