t-Test bei gepaarten Stichproben
Der gepaarte t-Test in SPSS ist recht einfach erklärt: Er vergleicht genau zwei Messungen, die voneinander abhängig sind, d.h. einen Zusammenhang aufweisen. Ein Zusammenhang wäre zum Beispiel die Befragung derselben Person zu zwei verschiedenen Zeitpunkten. Zum Beispiel könnte die Wirkung einer Diät untersucht werden, indem eine Person vor und nach der Diät gewogen wird. In diesem Fall wäre die abhängige Variableabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. (AV) das Gewicht der Person und die unabhängige Variable (UV) der Zeitpunkt der Messung (vor und nach der Diät). Es ist wichtig, dass immer die gleichen Personen und die gleichen Messzeitpunkte verwendet werden. Wenn es keinen Zusammenhang zwischen den Datenpunkten gibt, wählen wir den t-Test für unabhängige Stichproben.
Das Hauptziel des t-Tests ist es, Unterschiede zwischen Mittelwerten zu vergleichen. Eine Studie könnte folgendermaßen aussehen: Wir wollen die Wirkung einer Diät testen und messen deshalb vor der Studie das Gewicht aller Teilnehmenden mehrmals mit einer Waage. Wir gehen davon aus, dass die Teilnehmenden nach der Diät deutlich abgenommen haben. Nach der Testdiät, von der wir annehmen, dass sie drei Monate dauert, messen wir das Gewicht aller Teilnehmenden erneut und vergleichen die Differenz, also den Unterschied zwischen den Messzeitpunkten.
Gepaarter t-Test Voraussetzungen
- Die SkalenniveausSkalenniveau Das Skalenniveau bezieht sich auf den Typ von Daten, der in einer Studie erhoben wurde, und gibt an, wie die Daten in Bezug auf die Messbarkeit und die Möglichkeit zur Verwendung von Statistiken kodifiziert sind. der Variablen: Die unabhängige Variable ist nominalskaliert und hat zwei Ausprägungen, während die abhängige Variable intervallskaliert ist. In unserem Beispiel ist die unabhängige Variable (UV) der Messzeitpunkt 1 zu Beginn und der Messzeitpunkt 2 am Ende der Untersuchung. Die abhängige Variable (AV), das Messergebnis zu den Messzeitpunkten 1 und 2, ist intervallskaliert. Die Überprüfung der Skalenniveaus überprüfst du mit eigenen Überlegungen zu deinem Versuchsaufbau, ohne eine spezielle SPSS-Funktion zu verwenden. Lies die Anleitung zu Skalenniveaus hier, wenn du genauere Erklärungen benötigst, hier. Skalenniveau Anleitungen.
- Abhängige Messungen: Eine wichtige Voraussetzung für den gepaarten t-Test ist der Vergleich derselben Messobjekte. In unserem Fall werden dieselben Personen zu verschiedenen Zeitpunkten gemessen und nicht zwei Gruppen mit unterschiedlichen Messobjekten. Wenn es keinen Zusammenhang zwischen den Datenpunkten gibt, wählen wir den ungepaarter t-Test für unabhängige Stichproben.
- AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind.: Ausreißer sind Werte, die ungewöhnlich klein oder groß sind und sich negativ auf die Analyse auswirken, weil sie die Ergebnisse verzerren. Je weniger Ausreißer ein Datensatz enthält, desto besser. Hier ist eine Anleitung zur Prüfung von statistischen Ausreißer.
- NormalverteilungNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. : Normalverteilte Streuungen der abhängigen Variablen sind wünschenswert, aber nicht unbedingt erforderlich. Als Faustregel gilt, dass die Stichprobe größer als N=50 sein sollte. Wenn das Signifikanzniveausignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist. des Shapiro-Wilk-Tests größer als .05 ist, liegt eine Normalverteilung vor. Eine Anleitung zur Überprüfung der Normalverteilung findest du hier. Anleitung zur Normalverteilung und zum Shapiro-Wilk-Test.
Anmerkung: Der “Zeitpunkt der Messung” wird in der Regel als unabhängige Variable für einen gepaarten t-Test verwendet, dies ist jedoch nicht unbedingt der Fall. Stattdessen können zwei verschiedene Bedingungen verwendet werden.
Gepaarter t-Test in SPSS berechnen
Auswahl im Menü

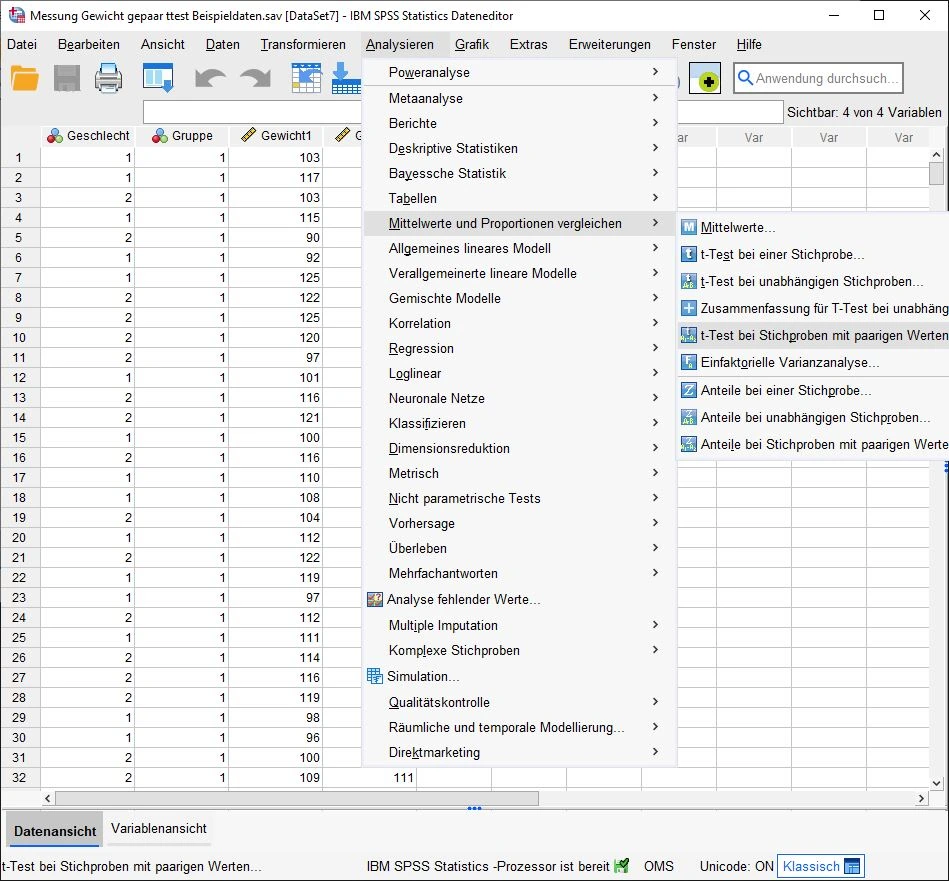
Wir klicken auf das obere Menü auf die Option Analysieren > Mittelwerte und Proportionen vergleichen > t-Test bei Stichproben mit paarigen Werten.
Variablen bei gepaarten t-Test zuordnen

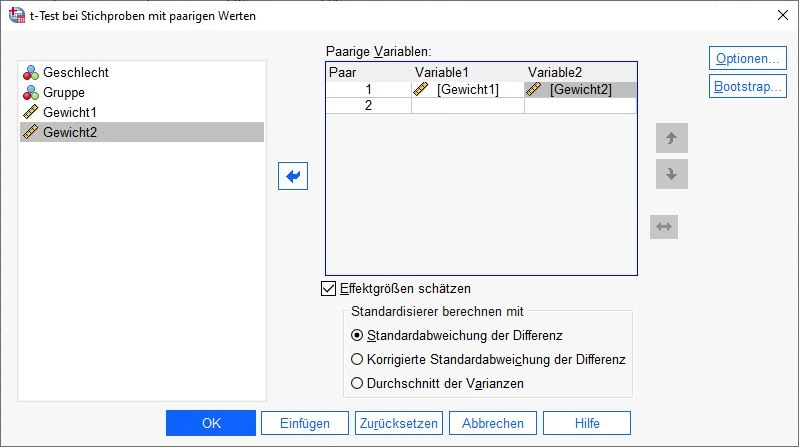
Es öffnet sich das Dialogfenster für den t-Test. Im linken Feld werden alle verfügbaren Variablen angezeigt. Wir klicken auf eine Variable, halten die Maustaste gedrückt und ziehen die Maus über die entsprechende Zelle in das Feld Paarvariablen. Wenn wir die Maustaste loslassen, haben wir die Variable in der Zelle platziert. Da wir den Unterschied zwischen den beiden Variablen messen wollen, platzieren wir die beiden Messwerte so, dass sie von SPSS als Variable1 und Variable2 erkannt werden.
In unserem Beispiel fügen wir die beiden Variablen für die Messzeitpunkte des Gewichts hinzu (Variable 1 und Variable 2).Wir setzen ein Häkchen bei Effektgrößen aus StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. der Differenz schätzen.
Dann klicken wir auf die Schaltfläche Optionen.
Gepaarter t-Test: Optionen

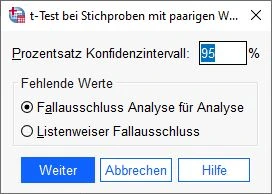
Bei Optionen können wir in der Regel die Standardeinstellungen belassen. Diese sehen so aus:
– Prozentsatz Konfidenzinterfall: 95%
– Fallauschluss Analyse für AnalyseAnschließend klicken wir auf Weiter.
Bereit zum Starten

Wir sind fertig und klicken auf OK.
Analyse der Ergebnisse: gepaarter t-Testin SPSS
Deskriptive Statistiken
SPSS gibt mehrere Tabellen aus. Die erste Tabelle zeigt deskriptive Gruppenstatistiken (Paired Samples Statistics).
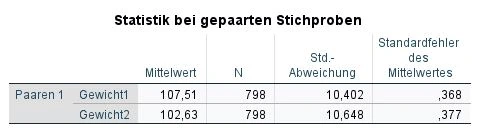
Gewicht 1 entspricht dem ersten Messzeitpunkt. In der Spalte Mittelwert (Mean) sehen wir, dass die Probanden im Durchschnitt 107,51 kg gewogen haben. N ist die Anzahl der Probanden. Die beiden anderen Spalten sind die Standardabweichung (Std. DeviationStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. ) und der Standardfehler des Mittelwertes (Std. Error Mean).
In dieser Tabelle sehen wir bereits, dass das Durchschnittsgewicht bei der zweiten Messung (Gewicht 2) von 107,51 kg auf 102,63 kg gesunken ist. In den nächsten Schritten wird geprüft, ob dieser Unterschied signifikant ist.
Tabelle: t-Test bei gepaarten Stichproben

Als nächstes schauen wir uns die Tabelle: Test bei gepaarten Stichproben an.
Wir konzentrieren uns auf die letzten drei Spalten mit dem T-Wert, dem df-Wert und dem Signifikanzniveau (Sig.).
Was bedeuten die Werte?
Der Buchstabe T vor der Klammer gibt an, dass der Berechnung eine t-Verteilung zugrunde liegt (t-Statistik). Die Zahl in Klammern gibt die Freiheitsgrade an (degree of freedom = df). Wenn sich der Stichprobenumfang ändert, ändern sich auch die Freiheitsgrade. Der T-Wert nach dem Gleichheitszeichen gibt den Wert in einem statistischen Nachschlagewerk zur Bestimmung der Signifikanz an (eher unwichtig). Nach dem Komma steht der p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist., der angibt, ob die Unterschiede zwischen den Messungen und Gruppen signifikant sind oder nicht. Häufig wird ein Signifikanzniveau von p = .05 angenommen. Das bedeutet, dass bei einem p-Wert von .05 oder weniger von Signifikanz und nicht von Zufall ausgegangen wird.
Zuerst betrachten wir die vier rechten Spalten der Tabelle. Mit diesen Werten stellen wir die Gleichung für den t-Test auf:
- Der T-Wert wird benötigt, um die Signifikanz zu bestimmen.
- df gibt die Freiheitsgrade in der Berechnung an.
- Signifikanz zweiseitiges p: gibt den p-Wert (Signifikanz) an.
Darstellung der Gleichung für den t-Test
t(df) = T-Wert, p= zweiseitige Signifikanz
t(797) = 34,660, p <.001
Effektstärken in SPSS berechnen

| Wert der Effektstärke Cohen´s d | Interpretation |
|---|---|
| |d| ≤ 0.2 | Kleiner Effekt |
| 0.2 < |d| ≤ 0.8 | mittlerer Effekt |
| |d| < 0.8 | Großer Effekt |
Ergebnisse publizieren
Es gab einen signifikanten Unterschied zwischen den gemessenen Gewichten vor und nach der Diät, t(797) = 34,660, p <.001

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn
Häufig gestellte Fragen und Antworten: Gepaarter t-Test in SPSS
Was ist ein t-Test einfach erklärt?
Der t-Test ist ein statistisches Verfahren, das verwendet wird, um festzustellen, ob es einen signifikanten Unterschied zwischen den Mittelwerten zweier Gruppen gibt. Er wird häufig verwendet, um zu prüfen, ob sich die Mittelwerte von Behandlungs- und Kontrollgruppen in einem Experiment signifikant voneinander unterscheiden. Es gibt verschiedene Arten von t-Tests, z. B. den einfachen t-Test und den paarweisen t-Test.
Was macht der t-Test?
Der t-Test vergleicht den Mittelwert einer Gruppe mit einem bekannten Wert oder dem Mittelwert einer anderen Gruppe und stellt dann fest, ob der Unterschied zwischen den Mittelwerten signifikant ist oder nicht. Ein signifikanter Unterschied bedeutet, dass es sich wahrscheinlich nicht um einen Zufall handelt und tatsächlich ein Unterschied zwischen den Gruppen besteht. Der t-Test liefert auch einen p-Wert, der angibt, wie wahrscheinlich es ist, dass ein Ergebnis auf Zufall beruht. Ein kleiner p-Wert bedeutet, dass es unwahrscheinlich ist, dass das Ergebnis auf Zufall beruht und dass ein signifikanter Unterschied zwischen den Gruppen besteht.
Wann braucht man T-Test?
T-Tests werden verwendet, wenn man sich dafür interessiert, ob es einen Unterschied zwischen den Mittelwerten zweier Gruppen gibt. Ein Beispiel wäre, wenn man die Wirksamkeit eines neuen Medikaments untersuchen möchte, indem man es einer Gruppe von Patienten verabreicht und ihre Ergebnisse mit denen einer Kontrollgruppe von Patienten vergleicht, die ein Scheinmedikament (Placebo) erhalten haben. Ein anderes Beispiel wäre, wenn man untersuchen möchte, ob es einen Unterschied in den durchschnittlichen Noten von Schülern gibt, die ein neues Schulbuch verwenden, im Vergleich zu Schülern, die ein traditionelles Schulbuch verwenden. Es gibt verschiedene Arten von T-Tests, je nachdem, ob die Daten normalverteilt sind, wie viele Gruppen es gibt, wie groß die Gruppen sind und andere Faktoren.
Gepaarter t-Test Beispiel
Du möchtest wissen, ob deine Müsliriegel wirklich durchschnittlich 100 Gramm wiegen, wie es auf der Verpackung steht. Dazu wiegst du 60 Riegel und vergleichst das tatsächliche Gewicht mit dem Gewicht, das sie haben sollten.