Was ist die HomoskedastizitätHomoskedastizität Homoskedastizität bezieht sich auf die Gleichmäßigkeit der Varianz der Residuen in einem statistischen Modell und bedeutet, dass die Varianz der Residuen über alle Werte der unabhängigen Variablen hinweg konstant ist. Eine Homoskedastizität wird als Vorbedingung für viele statistische Tests und Schätzverfahren angesehen und kann durch eine Gleichmäßigkeit der Streuung der Datenpunkte um die Regressionslinie in einem Scatterplot dargestellt werden.?
Die Homoskedastizität prüfen bedeutet, die Gleichmäßigkeit der Varianz (also die Streuung) der ResiduenResiduen Residuen sind die Abweichungen zwischen den beobachteten Daten und den durch ein statistisches Modell vorhergesagten Daten und werden verwendet, um die Anpassung des Modells an die Daten zu beurteilen und um mögliche Muster oder Trends in den Daten zu erkennen. Sie können auch verwendet werden, um die Validität und Zuverlässigkeit von Vorhersagemodellen zu überprüfen. eines Regressionsmodells zu untersuchen. Die Varianz der Residuen sollte in einem guten Modell gleich bleiben, unabhängig von den Werten der unabhängigen Variablen. Wenn die Varianz der Residuen jedoch von den Werten der unabhängigen Variablen abhängt, spricht man von Heteroskedastizität.
Was sind Residuen?
In der Statistik bezeichnet der Begriff “Residuum” (Mehrzahl Residuen) die Abweichung zwischen dem beobachteten Wert und dem vorhergesagten Wert in einem Regressionsmodell. Es handelt sich also um den Unterschied zwischen der tatsächlich beobachteten Variablen und der Variablen, die vom Modell vorhergesagt wurde. Die Residuen sind wichtig, um die Qualität eines Regressionsmodells zu beurteilen. Ein gutes Modell wird in der Regel kleine Residuen haben, was bedeutet, dass die Vorhersagen des Modells sehr genau sind. Auf der anderen Seite werden große Residuen als Anzeichen dafür betrachtet, dass das Modell nicht gut angepasst ist und möglicherweise verbessert werden muss.
Was sind die Folgen von Heteroskedastizität?
Eine Heteroskedastizität kann das Modell verzerren und die Schätzungen der Regressionskoeffizienten verfälschen, wodurch die Vorhersagen des Modells weniger zuverlässig werden. Daher ist es wichtig, die Homoskedastizität zu prüfen, um sicherzustellen, dass das Modell valide und zuverlässig ist. Es gibt verschiedene statistische Tests, die verwendet werden können, um die Homoskedastizität zu prüfen, wie beispielsweise der Breusch-Pagan-Test oder der White-Test.
In dieser Anleitung verwenden wir die einfachste Methode: das Streudiagramm.
Voraussetzung für den Test: Neue Variablen mit SPSS erstellen
Durch die Betrachtung der studentisierten Residiuen haben wir in SPSS ebenfalls einen Einblick auf die LinearitätLinearität Linearität bezieht sich auf die Beziehung zwischen zwei oder mehr Variablen, die durch eine gerade Linie dargestellt wird, bei der die Veränderung einer Variablen direkt proportional zur Veränderung der anderen Variable ist. von Variablen. Um diese Methode zu berechnen, ist es notwendig, bestimmte Variablen von SPSS vorab erstellen zu lassen (PRE_1 und SRE_1). In der Anleitung für die multiple lineare Regression beschreiben wir das Vorgehen.
Test der Homoskedastizität bei SPSS durch studentisierten Residuen
Prüfung der Homoskadastizität in SPSS durch studentisierte Residuen
Streudiagramm auswählen

Wir navigieren wie folgt: Grafik > Streu-/Punktdiagramm… und klicken auf die Option im Menü.
Dialogfenster Streudiagramm

Im Dialogfenster klicken wir auf “Einfaches Streudiagramm” und dann auf den Definieren-Knopf.
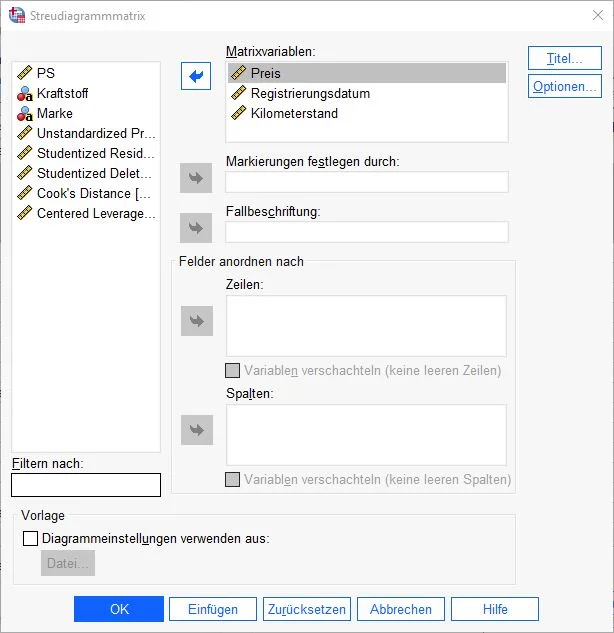
Dialogfenster “Einfaches Streudiagramm”

n dem Dialogfenster sehen wir mehrere Felder für Variablen.
– Im oberen Feld “Y-Achse” fügen wir die Variable SRE_1 ein (unstandardisierte vorhergesagte Werte).
– Im Feld “X-Achse” fügen wir die Variable “PRE_1” ein (studentisierte Residuen).Anschließend klicken wir unten auf den Knopf OK, um die Eingaben zu bestätigen.
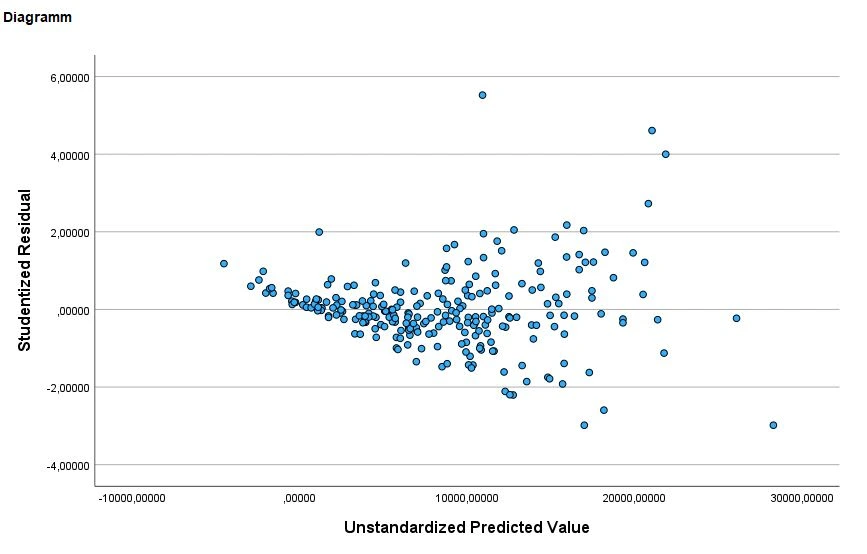
Analyse des Diagramms

SPSS hat uns ein Diagramm erstellt, dass uns die Verteilung der Datenpunkte für beide Variablen zeigt. Die Datenpunkte sollten bestenfalls gleichmäßig verteilt sein und sich möglichst wenig stauchen. In unserem Beispiel sind die Daten etwas gestaucht.
Hinweis: Es ist wichtig zu beachten, dass die Interpretation dieser Diagramme subjektiv sein kann. Es ist leicht, diese Diagramme zu überinterpretieren und jede Abweichung als potenziell problematisch zu betrachten, insbesondere für Menschen, die sich zum ersten Mal mit der Residualanalyse befassen.
Noch ein Hinweis: Besondere Vorsicht ist geboten, wenn Residuendiagramme für zu kleine Datensätze berechnet werden. Wenn zu wenige Daten vorliegen, können keine aussagekräftige Schlussfolgerungen gezogen werden.
Häufig gestellte Fragen und Antworten: Homoskedastizität in SPSS
Wie überprüft man Homoskedastizität?
Homoskedastizität bedeutet, dass die Varianz der Fehlerterm in einem Regressionsmodell konstant ist. Wenn die Varianz nicht konstant ist, wird als Heteroskedastizität bezeichnet.
Es gibt verschiedene Möglichkeiten, wie man Homoskedastizität überprüfen kann:
– Visualisierung: Eine Möglichkeit ist die Erstellung von Streudiagrammen mit Vorhersagefehlern auf der y-Achse und Vorhersagen auf der x-Achse. Wenn Homoskedastizität vorliegt, sollten die Streubereiche um den Mittelwert der Fehler gleichmäßig verteilt sein.
– Statistische Tests: Es gibt auch eine Reihe von statistischen Tests, die verwendet werden können, um Homoskedastizität zu überprüfen, wie z.B. der Goldfeld-Quandt-Test und der Breusch-Pagan-Test.
– Residuenplots: Eine weitere Möglichkeit ist die Erstellung von Residuenplots, die die Vorhersagefehler auf der y-Achse und die Vorhersagen auf der x-Achse zeigen. Wenn Homoskedastizität vorliegt, sollten die Residuen gleichmäßig um den Mittelwert verteilt sein.
Es ist wichtig zu beachten, dass keine Methode perfekt ist und dass es immer noch möglich ist, Heteroskedastizität zu übersehen. Du solltest daher immer mehrere Methoden verwenden, um sicherzustellen, dass du die Homoskedastizität deiner Daten richtig beurteilst.
Wie sieht Homoskedastizität aus?
Homoskedastizität bedeutet, dass die Varianz der Fehlerterm in einem Regressionsmodell konstant ist. Wenn die Varianz konstant ist, wird die Verteilung der Fehler gleichmäßig um den Mittelwert verteilt.
Eine Möglichkeit, Homoskedastizität zu visualisieren, ist die Erstellung von Streudiagrammen mit Vorhersagefehlern auf der y-Achse und Vorhersagen auf der x-Achse. Wenn Homoskedastizität vorliegt, werden die Streubereiche um den Mittelwert der Fehler gleichmäßig verteilt sein.
Eine andere Möglichkeit, Homoskedastizität zu visualisieren, ist die Erstellung von Residuenplots, die die Vorhersagefehler auf der y-Achse und die Vorhersagen auf der x-Achse zeigen. Wenn Homoskedastizität vorliegt, werden die Residuen gleichmäßig um den Mittelwert verteilt sein.
Was tun bei Heteroskedastizität SPSS?
Wenn du Heteroskedastizität in deinem Regressionsmodell festgestellt hast, gibt es einige Schritte, die du in SPSS unternehmen kannst, um das Problem zu lösen:
– Verwende robuste Standardfehler: Du kannst die Option “Robuster Standardfehler” in den Einstellungen des Regressionsdialogs auswählen, um robuste Standardfehler zu verwenden. Diese Standardfehler sind weniger anfällig für Auswirkungen von Heteroskedastizität als die Standardfehler, die standardmäßig verwendet werden.
– Verwende ein anderes Regressionsmodell: Du kannst auch ein anderes Regressionsmodell verwenden, das für Heteroskedastizität besser geeignet ist. Zum Beispiel könntest du ein GLS-Regressionsmodell (Generalized Least Squares) oder ein Regressionsmodell mit mittleren Quadratfehlern verwenden.
– Transformiere deine Daten: Du kannst auch versuchen, deine Daten zu transformieren, um Heteroskedastizität zu reduzieren. Zum Beispiel könntest du die logarithmische Transformation oder die Quadratwurzeltransformation verwenden.
Es ist wichtig zu beachten, dass keine dieser Lösungen perfekt ist und dass es immer noch möglich ist, dass Heteroskedastizität in deinem Regressionsmodell
Warum ist Homoskedastizität wichtig?
Homoskedastizität ist wichtig, weil sie eine Annahme vieler statistischer Tests und Analysen ist. Wenn Homoskedastizität in einem Regressionsmodell nicht vorliegt, können die Standardfehler der Schätzungen verzerrt werden und die Ergebnisse der Analyse werden möglicherweise nicht zuverlässig.
Die Homoskedastizität ist insbesondere wichtig bei der Interpretation von p-Werten und Confidence Intervallen. Wenn Homoskedastizität nicht vorliegt, können die p-WerteP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. und Confidence Intervalle unzuverlässig sein und falsche Schlussfolgerungen zulassen.
Es ist wichtig zu beachten, dass Homoskedastizität nur eine von vielen Annahmen ist, die bei der Durchführung von statistischen Analysen gemacht werden. Du solltest daher immer sicherstellen, dass du die Annahmen und Einschränkungen der verwendeten Analysemethoden verstehst und berücksichtigst.
Wann ist der Levene Test signifikant?
Der Levene-Test ist ein statistischer Test, der verwendet wird, um zu prüfen, ob die Varianzen in zwei oder mehr Gruppen gleich sind. Der Test ist signifikant, wenn die Varianzen der Gruppen nicht gleich sind.
Der Levene-Test wird durchgeführt, indem die Differenzen zwischen den Gruppenmitgliedern und dem Gruppenmittelwert berechnet werden. Diese Differenzen werden dann quadriert und die Summe der quadrierten Differenzen wird berechnet. Wenn die Summe der quadrierten Differenzen für die verschiedenen Gruppen signifikant unterschiedlich ist, bedeutet dies, dass die Varianzen der Gruppen nicht gleich sind und der Levene-Test ist signifikant.
Es ist wichtig zu beachten, dass der Levene-Test nur eine von vielen Methoden ist, um die Gleichheit der Varianzen zu prüfen. Du solltest daher immer mehrere Methoden verwenden, um sicherzustellen, dass du die Gleichheit der Varianzen deiner Daten richtig beurteilst.
Warum nach VarianzhomogenitätVarianzhomogenität Varianzhomogenität bezieht sich auf die Gleichmäßigkeit der Varianzen zwischen zwei oder mehr Gruppen und ist eine Vorbedingung für viele statistische Tests, die die Gleichheit der Gruppen untersuchen. Eine Varianzhomogenität wird angenommen, wenn die Varianzen der Gruppen ähnlich sind und bedeutet, dass keine Gruppe signifikant von den anderen Gruppen abweicht. Eine nicht vorhandene Varianzhomogenität kann dazu führen, dass die Ergebnisse von Tests verzerrt werden und kann darauf hinweisen, dass es in den Gruppen Unterschiede gibt, die berücksichtigt werden müssen. testen?
Varianzhomogenität bedeutet, dass die Varianzen in zwei oder mehr Gruppen gleich sind. Die Varianzhomogenität ist eine Annahme vieler statistischer Tests und Analysen, wie z.B. dem t-Test und dem ANOVA. Wenn die Varianzhomogenität nicht vorliegt, können die Standardfehler der Schätzungen verzerrt werden und die Ergebnisse der Analyse werden möglicherweise nicht zuverlässig sein.
Daher ist es wichtig, die Varianzhomogenität zu prüfen, bevor du einen statistischen Test oder eine Analyse durchführst, der diese Annahme macht. Wenn du die Varianzhomogenität nicht prüfst und die Annahme nicht erfüllt ist, können deine Ergebnisse falsch sein und zu falschen Schlussfolgerungen führen.
Es gibt verschiedene Methoden, um die Varianzhomogenität zu prüfen, wie z.B. den Levene-Test oder den Brown-Forsythe-Test. Du solltest immer mehrere Methoden verwenden, um sicherzustellen, dass du die Varianzhomogenität deiner Daten richtig beurteilst.
Was tun, wenn AutokorrelationAutokorrelation Autokorrelation ist ein Maß für den Zusammenhang zwischen den Werten einer Variablen über Zeit oder anderen Dimensionen hinweg und kann verwendet werden, um zu bestimmen, ob es in den Daten Muster oder Trends gibt. Eine hohe Autokorrelation bedeutet, dass die Werte der Variablen in der Regel in die gleiche Richtung gehen, während eine niedrige Autokorrelation darauf hinweist, dass die Werte der Variablen zufällig verteilt sind. vorliegt?
Autokorrelation tritt auf, wenn es eine Beziehung zwischen den Werten einer Zeitreihe gibt. Wenn Autokorrelation vorliegt, können die Standardfehler von Schätzungen verzerrt werden und die Ergebnisse von Analysen können unzuverlässig sein.
Wenn du Heteroskedastizität in deinem Regressionsmodell festgestellt hast, gibt es einige Schritte, die du in SPSS unternehmen kannst, um das Problem zu lösen:
– Verwende eine andere Analysemethode: Du kannst auch eine andere Analysemethode verwenden, die für Autokorrelation besser geeignet ist, wie z.B. die Zeitreihenanalyse oder die Strukturgleichungsmodellierung.
– Verwende ein anderes Regressionsmodell: Du kannst auch ein anderes Regressionsmodell verwenden, das für Heteroskedastizität besser geeignet ist. Zum Beispiel könntest du ein GLS-Regressionsmodell (Generalized Least Squares) oder ein Regressionsmodell mit mittleren Quadratfehlern verwenden.
– Transformiere deine Daten: Du kannst auch versuchen, deine Daten zu transformieren, um Heteroskedastizität zu reduzieren. Zum Beispiel könntest du die logarithmische Transformation oder die Quadratwurzeltransformation verwenden.
Es ist wichtig zu beachten, dass keine dieser Lösungen perfekt ist und dass es immer noch möglich ist, dass Autokorrelation in deinen Daten vorliegt. Du solltest daher immer sorgfältig überlegen, wie du Autokorrelation in deiner Analyse behandeln willst.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn