Was ist eine multiple lineare Regression?
Die multiple lineare Regression ist ein Verfahren zur Modellierung der Beziehung zwischen einer abhängigen Variablen (auch Zielvariable genannt) und mehreren unabhängigen Variablen (auch Prädiktoren genannt). Die multiple lineare Regression wird verwendet, um eine lineare Beziehung zwischen den Variablen zu schätzen und vorherzusagen, wie sich die abhängige Variableabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. aufgrund von Änderungen in den unabhängigen Variablen ändern wird. In dieser Anleitung berechnen wir die multiple lineare Regression in SPSS.
Ein Beispiel für die Verwendung einer multiplen linearen Regression wäre die Vorhersage des Einflusses von Alter, Geschlecht und Bildungsniveau auf das Einkommen einer Person. In diesem Fall wäre das Einkommen die abhängige Variable und Alter, Geschlecht und Bildungsniveau die unabhängigen Variablen.
Was berechnet eine multiple lineare Regression?
Eine multiple lineare Regression berechnet Koeffizienten für jede der unabhängigen Variablen (auch Prädiktoren genannt), die angeben, wie stark sich die abhängige Variable (auch Zielvariable genannt) bei einer Änderung der unabhängigen Variablen um eine Einheit ändert, wenn alle anderen Variablen konstant gehalten werden.
Die Berechnung der Koeffizienten erfolgt durch Minimierung der Summe der quadratischen Fehler (auch ResiduenResiduen Residuen sind die Abweichungen zwischen den beobachteten Daten und den durch ein statistisches Modell vorhergesagten Daten und werden verwendet, um die Anpassung des Modells an die Daten zu beurteilen und um mögliche Muster oder Trends in den Daten zu erkennen. Sie können auch verwendet werden, um die Validität und Zuverlässigkeit von Vorhersagemodellen zu überprüfen. genannt) zwischen den tatsächlichen Werten der abhängigen Variablen und den durch Schätzung der Koeffizienten vorhergesagten Werten.
Die multiple lineare Regression liefert auch eine Vorhersage für die abhängige Variable auf der Grundlage der angegebenen Werte der unabhängigen Variablen. Diese Vorhersage kann verwendet werden, um zu bestimmen, wie sich die abhängige Variable unter verschiedenen Bedingungen verändert.
Es ist wichtig zu beachten, dass die multiple lineare Regression nur dann gültig ist, wenn die Annahmen der linearen Regression erfüllt sind, wie z. B. eine lineare Beziehung zwischen den Variablen und eine NormalverteilungNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. der Residuen.
Multiple lineare Regression in der Anleitung
In der Statistik wird häufig versucht, den Einfluss von einer Variable auf eine andere zu erklären: Hängt der Wert eines Gebrauchtwagens von dem Alter des Autos ab? Das Problem bei einer solchen isolierten Betrachtung ist, dass in der Realität mehrere Einflüsse zeitgleich einwirken können. Der Wert eines Gebrauchtwagens könnte von dessen Alter, aber auch von den gefahrenen Kilometern abhängen – oder der Anzahl der Unfälle. Theoretisch gibt es eine beliebige Anzahl an Einflussfaktoren, die unterschiedlich stark einen Einfluss ausüben können.

Um eine präzisere Aussage über die Einflüsse von Variablen (Prädiktoren) auf eine Zielvariable (Kriterium) untersuchen zu können, wird deshalb in der Statistik eine multiple lineare Regressionsanalyse angewandt. Sie erweitert die einfache lineare Regression mit zusätzlichen Prädiktoren. In unserem Beispiel ist der Wert des Gebrauchtwagens die Zielvariable und als Prädiktoren kommen mehrere Prädiktoren in Betracht: der Kilometerstand, das Alter, Motorstärke (PS), Spritverbrauch, Automarke und Ausstattungsmerkmale wie Kraftstoff (Benzin/Diesel/Elektro), Schadstoffklasse und so weiter.
Mit der multiplen linearen Regression versuchen Statistiker zu verstehen, welche Prädiktoren einen signifikanten Einfluss auf das Kriterium ausüben. Wir wollen herausfinden, wie stark der Einfluss ist und welche Variablen weniger wichtig zur Berechnung eines Zusammenhangs sind. Das Ziel ist es eine mathematische Gleichung (Vorhersagemodell) zu erstellen, mit dem der Wert eines Gebrauchtwagens mit den Daten wie Alter und Kilometerstand möglichst präzise vorhergesagt werden kann. Wie diese Gleichung aussehen kann und wie die Präzision der Gleichung (Varianzaufklärung) gemessen wird, erklärt diese Anleitung am Ende Schritt für Schritt.
Wo finde ich den Beispieldatensatz für die Berechnung in SPSS?
Der Beispieldatensatz ist hier.
Die Voraussetzungen für eine multiple lineare Regression
Ergebnisse lassen sich dank SPSS relativ schnell produzieren. Der Unterschied zwischen einer guten und schlechten Analyse ist die Überprüfung, ob bestimmte Rechenoperationen überhaupt durchführbar sein dürfen und was die Präzision der Ergebnisse beeinträchtigen könnte.
- SkalenniveauSkalenniveau Das Skalenniveau bezieht sich auf den Typ von Daten, der in einer Studie erhoben wurde, und gibt an, wie die Daten in Bezug auf die Messbarkeit und die Möglichkeit zur Verwendung von Statistiken kodifiziert sind.: Die Zielvariable (Kriterium) muss eine abhängige Variable und intervallskaliert sein (was bedeutet das?). Die Prädiktoren müssen mindestens zwei unabhängige Variablen sein. Die Prädiktoren können entweder nominalskaliert oder mindestens intervallskaliert sein. Mehr über Skalennivieaus erfahren.
- LinearitätLinearität Linearität bezieht sich auf die Beziehung zwischen zwei oder mehr Variablen, die durch eine gerade Linie dargestellt wird, bei der die Veränderung einer Variablen direkt proportional zur Veränderung der anderen Variable ist. : Bei einer multiplen linearen Regressionsanalyse müssen die untersuchten Variablen einen linearen Zusammenhang aufweisen. Falls dies nicht der Fall ist, kann es zu Unter- oder Überschätzungen bei dem Vorhersagemodell kommen. Anleitung lineare Beziehung prüfen.
- AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind.: Die multiple lineare Regression ist empfindlich gegenüber Ausreißern, weshalb der Datensatz auf Ausreißer hin überprüft werden sollte. Anleitung Ausreißer prüfen.
Es gibt weitere Voraussetzungen für eine multiple lineare Regression, die wir beachten müssen. Diese lassen sich am besten analysieren, wenn wir die ersten Berechnungen in SPSS durchgeführt haben. Und genau das passiert im nächsten Schritt.
Multiple lineare Regression in SPSS durchführen
Berechnung der Multiplen linearen Regression in SPSS durchführen
Multiple lineare Regression in SPSS auswählen

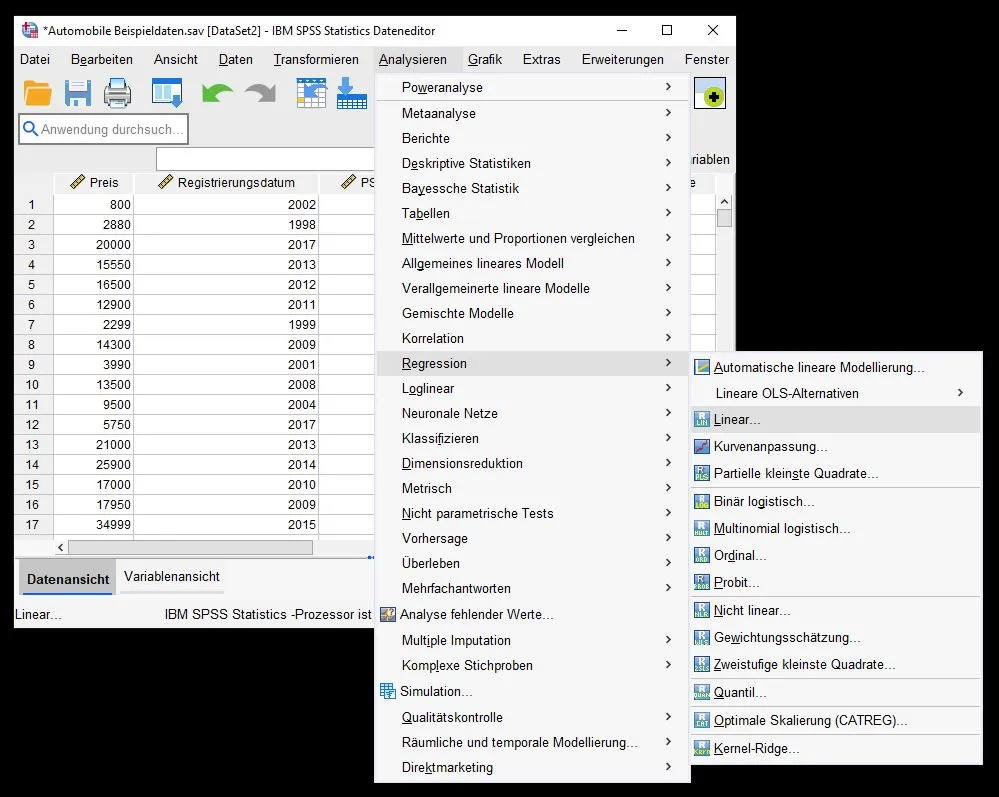
Um eine multiple lineare Regression auszuführen, gehen wir zu Analysieren > Regression > Linear…
Dialogfenster: Lineare Regression

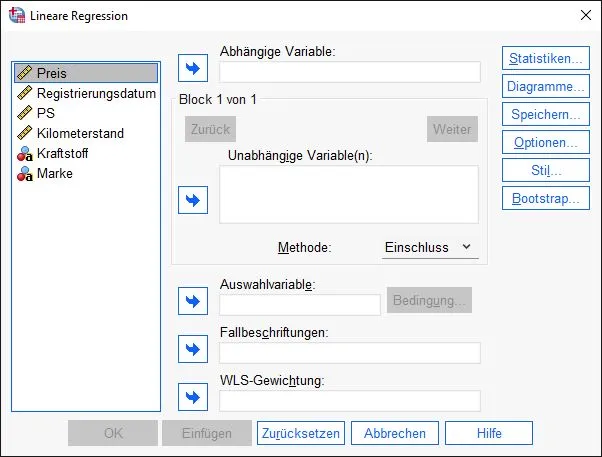
Es öffnet sich das Lineare Regression Dialogfenster. Ein Dialogfenster ist ein Fenster, das vom System geöffnet wurde und auf eure Eingaben wartet.
Auf der linken Seite werden unsere verfügbaren Variablen aus dem Datensatz angezeigt. Auf der rechten Seite sehen wir mehrere Felder, in die wir Variablen verschieben können. Es gibt zwei Möglichkeiten, die Variablen zu verschieben:
Drag-and-drop: Wir klicken wir auf eine Variable mit der linken Maustaste, halten die Maustaste gedrückt und ziehen sie in das gewünschte Feld, um dann die Maustaste loszulassen.
Per Knopf: Wir markieren mit der linken Maustaste eine Variable und klicken erneut mit der linken Maustaste auf den Pfeil, der nach rechts zeigt und sich neben den rechten Feldern befindet.
Variablen in SPSS zuordnen

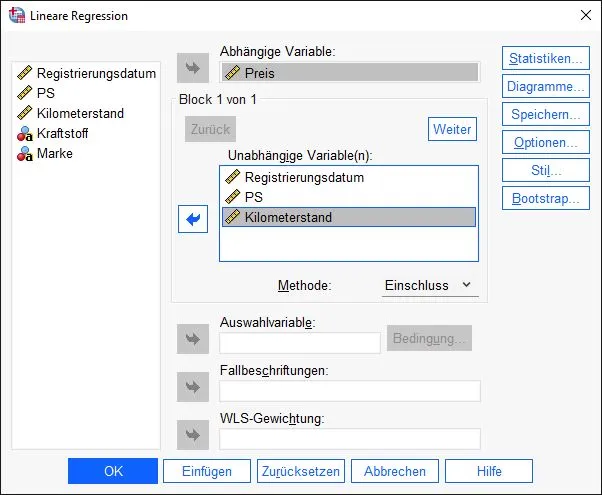
Jetzt setzen wir die Regression zusammen. Hierfür benötigen wir eine abhängige Variable. Das Ziel der multiplen linearen Regression ist es, die Varianz der Werte einer abhängigen Variable durch mehrere unabhängige Variablen zu erklären.
Für unser Beispiel wollen wir den Preis eines Gebrauchtwagens durch Eigenschaften wie PS, Kilometerstand und Registrierungsdatum erklären. Deshalb ist der Preis die unabhängige Variable. Die anderen Variablen kommen in das Feld “unabhängige Variable(n)”.
Weitere Einstellungen durchführen

Wir befinden uns noch immer in der gleichen Dialogbox. Bevor wir die Berechnungen starten, erlaubt uns SPSS Einstellungen vorzunehmen. Diese Einstellungen befinden sich auf der rechten Seite der Dialogbox hinter mehreren Knöpfen.
Wir klicken auf der rechten Seite der Dialogbox auf die Option “Statistiken”
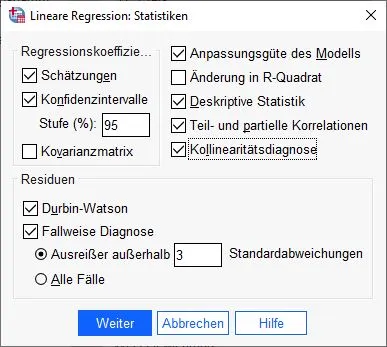
Lineare Regression: Statistiken konfigurieren

Auf den ersten Blick sehen die Einstellungen unübersichtlich aus. Das liegt daran, dass SPSS viele Berechnungen kennt. Wir benötigen bestimmte Statistiken, um unsere Ergebnisse genauer zu analysieren und Voraussetzungen zu überprüfen. Aus diesem Grund wählen wir die folgenden Optionen an:
Schätzungen, KonfidenzintervalleKonfidenzintervalle Konfidenzintervalle sind Schätzungen der wahren Population, die angeben, mit welcher Wahrscheinlichkeit sich die wahre Population innerhalb eines bestimmten Bereichs befindet. Sie werden verwendet, um die Unsicherheit von Schätzungen auszudrücken und die Stabilität von Statistiken zu beurteilen und werden häufig in der Statistik und der Datenanalyse verwendet. (95%), Anpassungsgüte des Modells, Deskriptive Statistik, Teil- und partielle KorrelationenKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird., Kollinearitätsdiagnose, Durbin-Watson und Fallweise Diagnose (3).Wir haben viel vor! Wir klicken auf Weiter, um die Auswahl zu bestätigen.
Weitere Einstellungen durchführen

Wir landen wieder auf der Dialogbox und wählen weitere Einstellungen. Im nächsten Schritt klicken wir auf “Diagramme” auf der rechten Seite.
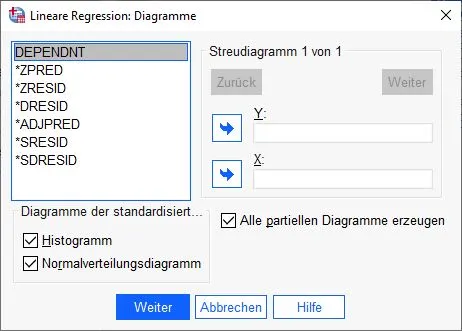
Multiple lineare Regression: Diagramme einstellen

Das nächste Dialogfenster für Diagramme erscheint. Im unteren Bereich klicken wir auf die Kontrollkästchen Histogramm, Normalverteilungsdiagramm und alle partiellen Diagramme erzeugen.
Wir bestätigen die Eingaben und klicken auf den Knopf Weiter.
Weitere Einstellungen durchführen

Zurück zur ursprünglichen Dialogbox. Hier klicken wir auf die Einstellung “Speichern”, um neue Variablen zu erstellen.
Dialogfenster Lineare Regression Speichern
In dieser Dialogbox wählen wir folgende Kontrollkästchen an:
Vorhergesagte Werte: nicht standardisiert.
Residuen: Studentisiert
Residuen: Studentisiert, ausgeschlossen
Distanzen: Cook und Hebelwerte
Kovarianzmatrix speichernWir bestätigen mit einem Klick auf Weiter.
Startklar: wir können die Berechnung in SPSS beginnen

Geschafft. Wir sind startklar und klicken auf OK, um SPSS die multiple lineare Regression berechnen zu lassen.
Die Analyse der Ergebnisse folgt im nächsten Schritt.
Weitere Voraussetzungen der multiplen linearen Regression checken
Bevor wir uns auf die Ergebnisse stürzen, kontrollieren wir weitere Voraussetzungen für die Regression in SPSS. Die notwendigen Daten sehen wir in den neuen Tabellen, die wir im letzten Schritt erzeugt haben. Sie alle befinden sich in der Ausgabe.
Voraussetzung: Unabhängigkeit der Residuen
Wenn wir Daten analysieren, gehen wir davon aus, dass die untersuchte Stichprobe absolut zufällig getestet wurde. Das bedeutet, dass die Auswahl der und alle Elemente und deren Kombination keinem Schema folgt. Wenn dies nicht der Fall ist, verliert unser finales Modell an Aussagekraft (AutokorrelationAutokorrelation Autokorrelation ist ein Maß für den Zusammenhang zwischen den Werten einer Variablen über Zeit oder anderen Dimensionen hinweg und kann verwendet werden, um zu bestimmen, ob es in den Daten Muster oder Trends gibt. Eine hohe Autokorrelation bedeutet, dass die Werte der Variablen in der Regel in die gleiche Richtung gehen, während eine niedrige Autokorrelation darauf hinweist, dass die Werte der Variablen zufällig verteilt sind.). In SPSS testen wir die Autokorrelation der ersten Ordnung und klären ab, ob ein Residuum mit seinem direkten Nachbarn korreliert. Gerade bei Tests mit Zeitreihenanalysen ist eine Prüfung der Autokorrelation wichtig.
Was ist ein Residuum?
In der Statistik bezeichnet der Begriff “Residuum” die Abweichung zwischen dem beobachteten Wert und dem vorhergesagten Wert in einem Regressionsmodell. Es handelt sich also um den Unterschied zwischen der tatsächlich beobachteten Variablen und der Variablen, die vom Modell vorhergesagt wurde. Die Mehrzahl von Residuum sind Residuen.
Die Residuen sind wichtig, um die Qualität eines Regressionsmodells zu beurteilen. Ein gutes Modell wird in der Regel kleine Residuen haben, was bedeutet, dass die Vorhersagen des Modells sehr genau sind. Auf der anderen Seite werden große Residuen als Anzeichen dafür betrachtet, dass das Modell nicht gut angepasst ist und möglicherweise verbessert werden muss.
Durbon-Watson-Statistik
Die Unabhängigkeit der Residuen prüfen wir in SPSS mit der Durban-Watson-Statistik. In der oberen Anleitung haben wir bei Statistiken in Schritt 5 dort einen Haken gesetzt. Die Tabelle mit den Daten befindet sich in der Ausgabe und heißt “Modellzusammenfassung“.

Wir betrachten die Spalte ganz rechts mit dem Namen “Durbin-Watson-Statistik”. Eine Autokorrelation liegt im Grunde vor, wenn …
- der Wert höher als 2 ist
- der Wert niedriger als -2
Wenn wir in der Prüfung einen Wert zwischen 2 und -2 erzielen, können wir davon ausgehen, dass keine Autokorrelation auftritt. Die Durbin-Watson-Statistik kann theoretisch einen Wert von 4 bis -4 annehmen.
In unserem Beispiel sehen wir einen Wert von 1,622. Eine Autokorrelation tritt nach Durbin-Watson-Statistik nicht auf.
Was tun, wenn es eine Autokorrelation gibt?
Falls eine Autokorrelation stattfindet, sollte ein weiteres Verfahren verwendet werden, wie Heteroskedastizität-und-Autokorrelations-konsistente Schätzer (Newey-West-Schätzer oder HAC).
Voraussetzung: Keine Multikollinearität
Wenn zwei oder mehr Variablen eine sehr hohe KorrelationKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird. haben, können wir davon ausgehen, dass sie ähnliche “Informationen” beinhalten und die Berechnung der Regressionskoeffizienten beeinträchtigt wird. Deshalb sollte unser finales Modell Prädiktoren verwenden, die sich nicht zu ähnlich sind (Multikollinearität).
Prüfung der Multikollinearität durch Korrelationstabellen
Eine relativ einfache Methode, Multikollinearität zu messen, ist die Prüfung der Korrelationen. In der Ausgabe blicken wir deshalb auf die Tabelle Korrelationen.
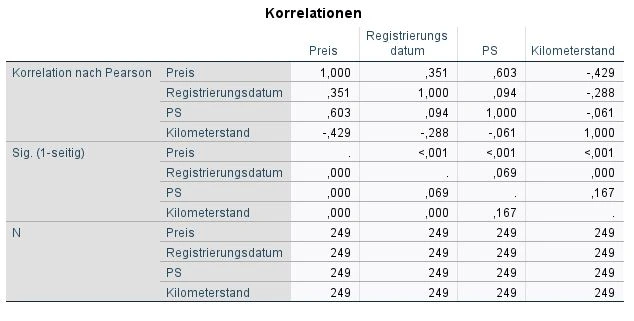
In dieser Tabelle blicken wir auf die oberen Zeilen, die zu “Korrelation nach Pearson” gehören: Preis, Registrierungsdatum, PS und Kilometerstand. Diese Variablen befinden sich in den Spalten und Zeilen. Das bedeutet, dass wir schnell die Korrelationen zwischen den einzelnen Variablen vergleichen möchten.
Die Werte für Korrelationen können von 1 bis -1 reichen. Eine 1 meint eine perfekte Korrelation. -1 ist eine perfekte negative Korrelation und 0 bedeutet keine Korrelation.
Kurz erklärt: Was ist eine Korrelation?
In der Statistik bezeichnet der Begriff “Korrelation” das Ausmaß, in dem zwei Variablen miteinander in Beziehung stehen. Wenn zwei Variablen korreliert sind, bedeutet dies, dass sie auf irgendeine Weise miteinander verbunden sind und dass eine Veränderung in einer Variable wahrscheinlich auch eine Veränderung in der anderen Variable verursacht. Es gibt verschiedene Arten von Korrelationen, wie positive, negative und keine Korrelation.
Eine positive Korrelation bedeutet, dass, wenn eine Variable ansteigt, die andere Variable ebenfalls ansteigt. Eine negative Korrelation bedeutet, dass, wenn eine Variable ansteigt, die andere Variable abnimmt. Keine Korrelation bedeutet, dass es keine Beziehung zwischen den beiden Variablen gibt.
Es ist wichtig zu beachten, dass Korrelation nicht gleichbedeutend mit KausalitätKausalität Kausalität bezieht sich auf den Zusammenhang zwischen zwei oder mehr Ereignissen oder Variablen, bei dem ein Ereignis oder eine Variable (die Ursache) das andere Ereignis oder die andere Variable (die Wirkung) verursacht. ist. Das heißt, nur weil zwei Variablen miteinander korreliert sind, bedeutet das nicht unbedingt, dass eine Variable die andere direkt beeinflusst. Es gibt möglicherweise andere Faktoren, die die Beziehung zwischen den Variablen beeinflussen.
Ein Beispiel für eine positive Korrelation wäre die Beziehung zwischen Alter und Erfahrung. In diesem Fall könnte man vermuten, dass je älter jemand ist, desto mehr Erfahrung hat er oder sie in der Regel. Wenn man also das Alter als abhängige Variable betrachtet und die Erfahrung als unabhängige Variable, dann wäre die Korrelation zwischen diesen beiden Variablen positiv. Das heißt, wenn das Alter zunimmt, nimmt die Erfahrung wahrscheinlich auch zu und umgekehrt.
Ein Beispiel für eine negative Korrelation wäre die Beziehung zwischen Körpergewicht und Bewegung. In diesem Fall könnte man vermuten, dass je mehr jemand sich bewegt, desto weniger wahrscheinlich ist es, dass er oder sie übergewichtig ist. Wenn man also die Menge an Bewegung als abhängige Variable betrachtet und das Körpergewicht als unabhängige Variable, dann wäre die Korrelation zwischen diesen beiden Variablen negativ. Das heißt, wenn das Körpergewicht zunimmt, nimmt die Menge an Bewegung wahrscheinlich ab und umgekehrt.
Es ist jedoch wichtig zu beachten, dass dies nur eine Vermutung ist und es weitere Faktoren geben könnte, die die Beziehung zwischen diesen beiden Variablen beeinflussen. Um sicherzustellen, dass es tatsächlich eine negative Korrelation gibt, müsste man die Daten analysieren, um die Stärke und Richtung der Beziehung zu bestimmen.
Sobald zwei Variablen eine Korrelation von 0,7 oder höher haben, können wir von einer Multikollinearität ausgehen. Das gilt ebenfalls für negative Werte von -0,7 und kleiner.
In unserem Beispiel gibt es Korrelationen von 0.351, 0.603, -0.429, usw. Eine Multikollinearität können wir deshalb ausschließen.
Prüfung der Multikollinearität durch Toleranz und VIF
Eine weitere Methode ist die Prüfung durch Toleranz und VIF in der Tabelle Koeffizienten (VIF steht für variance influence factor).

Wir blicken ganz rechts auf die Spalten Kollinearitätsstatistik “Toleranz” und “VIF”. Multikollinearität ist vorhanden, wenn eine der beiden Bedingungen erfüllt ist:
- der VIF Wert ist über 10
- der Toleranz Wert ist unter 0.1
In unserem Beispiel trifft das auf keine der Variablen (PS, Kilometerstand, Registrierungsdatum) zu. Eine Multikollinearität können wir ausschließen.
Was tun, wenn es eine Multikollinearität gibt?
Wenn Multikollinearität festgestellt wird, dann gibt es Variablen, die sich zu ähnlich sind. Hier solltest du dich fragen, ob es Sinn macht, zwei Variablen einzusetzen, die im Grunde das Gleiche aussagen. Aus diesem Grund kann es sinnvoll sein, eine Variable zu entfernen. Wenn du zwei oder mehr Prädiktoren hast, ist das die einfachste Lösung.
Multikollinearität ist ein Indikator, dass dein Datensatz Variablen hat, die sich zu ähnlich sind. Statistikexperten wenden in diesen Fall gerne die Hauptkomponentenanalyse (Faktorenanalyse) an. Mithilfe dieser Methode können wir aus mehreren Variablen eine Variable schaffen und Informationen verdichten. Hier ist die Anleitung zur Hauptkomponentenanalyse.
Voraussetzung: HomoskedastizitätHomoskedastizität Homoskedastizität bezieht sich auf die Gleichmäßigkeit der Varianz der Residuen in einem statistischen Modell und bedeutet, dass die Varianz der Residuen über alle Werte der unabhängigen Variablen hinweg konstant ist. Eine Homoskedastizität wird als Vorbedingung für viele statistische Tests und Schätzverfahren angesehen und kann durch eine Gleichmäßigkeit der Streuung der Datenpunkte um die Regressionslinie in einem Scatterplot dargestellt werden. der Residuen
Die Varianz der Residuen sollte bestenfalls gleich sein, damit in der späteren Gleichung bestimmte Bereiche (hochpreisige Autos, niedrigpreisige Autos) nicht unterschiedlich genaue Aussagen haben. Unser finales Modell sollte bestenfalls in allen Bereichen präzise Ergebnisse berechnen können.
Um die Homoskedastizität der Residuen in SPSS zu prüfen, empfehlen wir diese Anleitung.
Voraussetzung: Normalverteilung der Residuen
Residuen müssen normalverteilt, homoskedastisch und unabhängig sein. Das ist für die Validierung der Ergebnisse wichtig, so wird die Zuverlässigkeit der Ergebnisse gesichert.
Histogramm der Residuen als Analysemethode
Dieses Histogramm zeigt die Häufigkeit und die Verteilung der Residuen für die Variable Preis.
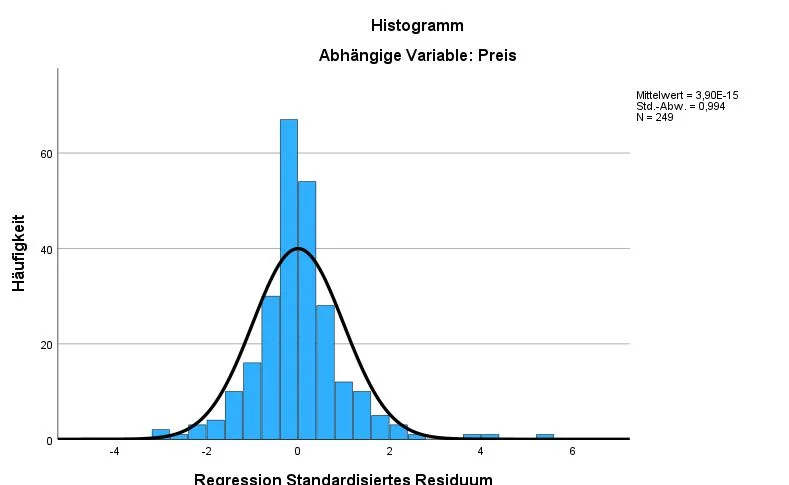
In unserem Beispiel liegen die Residuen für die Variable Preis recht deutlich auf dem Verlauf der Normalverteilung, was gut ist. Oben rechts sehen wir den Mittelwert, die StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. und Anzahl der Fälle (N). Der Mittelwert sollte am besten bei ca. 0 sein und die Standardabweichung bei 1. Die Anzahl der Fälle sollte ebenfalls ausreichend hoch sein.
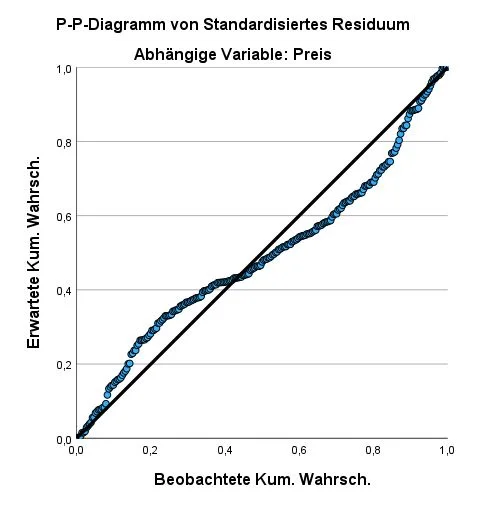
Methode: P-P-Plot Diagramm
Dieses P-P-Plot Diagramm zeigt, dass die beobachtbaren Werte (Kreise) recht nah an den erwartbaren Werten liegt (Linie). Es ist nicht perfekt, aber noch akzeptabe. Je näher die beobachtbaren Werte auf der Linie liegen, desto besser. Wenn die beobachtbaren Werte recht weit entfernt sind, spricht das gegen eine Normalverteilung.
Methode: Shapiro-Wilk-Test
Die Normalverteilung kann mittels Shapiro-Wilk-Test mit der Variable SRE_1 stattfinden.
Hier gibt es die Anleitung für den Shapiro-Wilk-Test.
Was passiert, wenn die Normalverteilung nicht gegeben ist?
- Du führst die Rechnung einfach fort und verweist bei denen Ergebnissen darauf. In der Regel ist die multiple lineare Regression recht robust gegen eine Verletzung und deine Ergebnisse sind immer noch nutzbar.
- Alternativ können deine Daten transformiert werden. Das Problem beim Transformieren ist, dass es zu einer Verschlimmbesserung kommen kann, die in der Statistik ebenfalls problematisch ist.
- Alternativ kannst du bei SPSS BootstrappingBootstrapping Bootstrapping ist eine Methode der Datenanalyse, bei der aus einer bestehenden Stichprobe wiederholt neue Stichproben gezogen werden, um die Unsicherheit von Schätzungen und die Stabilität von Statistiken zu untersuchen. Durch das Bootstrapping wird die Verteilung der Schätzungen simuliert und es können Konfidenzintervalle berechnet werden, die eine Aussage über die Wahrscheinlichkeit machen, dass die wahre Population innerhalb eines bestimmten Bereichs liegt. nutzen. Diese Option ist bei den Einstellungen einer multiplen linearen Regression verfügbar.
- Es lassen sich andere Regressionsmethoden wie Constrained Nonlinear Regression (CNLR) durchführen. Sie ist wesentlich robuster, aber auch komplexer in der Durchführung.
Analyse der Ergebnisse
Analyse der Varianzaufklärung unseres Regressionsmodells
Wir blicken auf die Tabelle Modellzusammenfassung und dort die Spalten R, R² und korrigiertes R².

- R ist der Pearson-Korrelationskoeffizient, der die Stärke und Richtung einer linearen Beziehung zwischen zwei Variablen misst. R liegt immer zwischen -1 und 1, wobei -1 eine perfekte negative Korrelation, 1 eine perfekte positive Korrelation und 0 keine Korrelation bedeutet.
- R² ist die Varianzerklärung und gibt an, wie viel der Variation in der abhängigen Variable durch die unabhängige Variable erklärt wird. R² liegt immer zwischen 0 und 1, wobei 1 bedeutet, dass die unabhängige Variable die gesamte Variation in der abhängigen Variable erklärt, und 0 bedeutet, dass die unabhängige Variable keine Erklärung für die Variation in der abhängigen Variable bietet.
- Korrigiertes R² ist eine angepasste Version von R², die berücksichtigt, wie viele Variablen in der Regression analysiert wurden. Es wird verwendet, um zu vergleichen, wie gut verschiedene Regressionsmodelle die abhängige Variable erklären, und gibt an, wie viel der Variation in der abhängigen Variable durch die unabhängigen Variablen erklärt wird, wenn die Anzahl der Variablen berücksichtigt wird. Wie R² liegt korrigiertes R² immer zwischen 0 und 1.
Eine Interpretationshilfe gibt uns Cohen:
| |R| | |R²| und korrigiertes |R²| | Interpretation nach Cohen |
|---|---|---|
| .10 | .02 | Schwache Korrelation |
| .30 | .13 | Moderate Korrelation |
| .50 | .26 | Starke Korrelation |
Vergisst nicht, dass das nur Richtwerte sind und die Interpretation oft recht komplexer ist. Beispielsweise können in neurowissenschaftlichen Studien kleinere R ein starkes Ergebnis sein, weil die Sensorik bestimmte Limitierungen haben kann. Häufig empfiehlt es sich, auf ähnliche Studien von anderen Forschern zu blicken. So erhältst du ein besseres Gefühl, welche Erwartungshaltung du haben solltest.
In unserem Beispiel hat R² den Wert von .555 und ein korrigiertes R² von .550, was ein hervorragendes Ergebnis ist.
Analyse der Signifikanz des Modells
Wir blicken auf die Tabelle ANOVA und dort auf die Spalte ganz rechts: Signifikanz (Sig.).
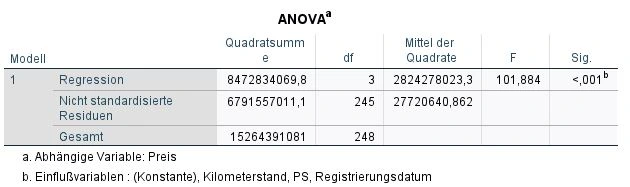
Wir stellten uns die Frage, ob unser Ergebnis rein zufällig war oder es einen signifikanten Zusammenhang gibt. In der Statistik wird die Signifikanz mit der Variable “p” bezeichnet. Je kleiner der p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. ist, desto höher ist die Signifikanz. Die Signifikanz kann theoretisch nicht Null ergeben, weshalb uns SPSS für sehr kleine Werte ein p <.001 ausgibt. In unserem Beispiel ist das Ergebnis hochsignifikant.
Ob die Ergebnisse in deiner Studie signifikant sind oder nicht, hängt von dem verwendeten Signifikanzniveausignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist.. Das Signifikanzniveau wird mit dem griechischen Buchstaben “α” abgekürzt und liegt in der Regel bei α= .05. Ein Signifikanzniveau von 5 % meint, dass wir mit einer Fehlerwahrscheinlichkeit von 5 % das Ergebnis des Modells akzeptieren.
Wie hoch sollte das Signifikanzniveau sein?
Das Signifikanzniveau ist der Schwellenwert, der festlegt, wie wahrscheinlich es sein muss, dass ein Ergebnis aufgrund eines Zufalls auftritt, bevor man annimmt, dass es aufgrund einer tatsächlichen Beziehung zwischen zwei Variablen auftritt. Es wird in der Regel als alpha-Wert festgelegt und ist in der Regel auf 0,05 oder 0,01 festgelegt. Ein niedrigeres Signifikanzniveau bedeutet, dass man strengere Anforderungen hat, bevor man annimmt, dass ein Ergebnis signifikant ist, während ein höheres Signifikanzniveau bedeutet, dass man weniger strenge Anforderungen hat. Die Wahl des richtigen Signifikanzniveaussignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist. hängt von den Zielen der Studie und den Risiken ab, die man bereit ist einzugehen, dass man falsch negativ oder falsch positiv ist.
Die Regressionsgleichung
Die Regressionsgleichung ist das Herzstück unseres Modells. Es ist die mathematische Formel, um Werte für unsere Zielvariable vorherzusagen.
Was bedeutet die Regressionsgleichung?
In der Regressionsanalyse wird eine Regressionsgleichung verwendet, um die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu beschreiben. Die Regressionsgleichung sieht in der allgemeinen Form wie folgt aus:
y = b0 + b1 * x1 + b2 * x2 + ... + bn * xnIn dieser Gleichung ist y die abhängige Variable, die Vorhersagevariable oder diejenige, die erklärt werden soll, und x1, x2, …, xn sind die unabhängigen Variablen oder die Prädiktoren, die verwendet werden, um y zu erklären. b0 ist der y-Achsenabschnitt und b1, b2, …, bn sind die Regressionskoeffizienten (auch Steigungskoeffizienten genannt) für die unabhängigen Variablen. Die Regressionskoeffizienten geben an, wie sehr sich y ändert, wenn sich eine unabhängige Variable um 1 ändert, während alle anderen Variablen konstant bleiben.
Die Regressionsgleichung wird verwendet, um Vorhersagen für y zu machen, indem man die bekannten Werte für die unabhängigen Variablen einsetzt
Koeffiziententabelle analysieren
Wir blicken auf die Tabelle Koeffizienten in SPSS und dort auf die Spalte “Regressionskoeffizienten B”. In jeder Zeile sehen wir hier die Werte für unsere abhängigen Variablen: Registrierungsdatum, PS und Kilometerstand und die Konstante.

Zum Beispiel, wenn man wissen möchte, wie sich die Anzahl der gefahrenen Kilometer auf den Wert eines Gebrauchtwagens auswirkt. In diesem Fall könnte man eine Regressionsgleichung verwenden, um die Beziehung zwischen diesen beiden Variablen zu beschreiben. Die Regressionsgleichung wird verwendet, um Vorhersagen für den durchschnittlichen Preis bei einem Gebrauchtwagen zu berechnen.
Unsere Gleichung kann sogar mehr: Wenn wir das Registierungsdatum, die PS Zahl und den Kilometerstand eingeben, können wir recht präzise den Preis für einen Gebrauchtwagen bestimmten. Wir müssen lediglich die untere Formel verwenden:
Preis = 220,998 * Registrierungsdatum + 89,952 * PS - 0,069 * Kilometerstand – 439666,563
Konkret sagt uns unsere Gleichung
- Je höher das Registrierungsdatum, desto höher ist Preis. Für jedes Jahr steigt der Preis um 220,998 EUR.
- Je höher die PS Zahl, desto höher ist der Preis. Für jedes PS mehr steigt der Preis um 89,952 EUR.
- Je niedriger der Kilometerstand, desto höher ist der Preis. Für jeden gefahrenen Kilometer sinkt der Preis um 0,069 EUR.
Wie kann ich mit der Gleichung den Preis berechnen?
7115,10 = 220998 * 2010 + 89952 * 90 - 0,069 * 80000 - 439666,563Wir testen unsere Regressionsgleichung. Angenommen, ich habe einen Gebrauchtwagen mit dem Registrierungsdatum 2010 , mit 90 PS und 80.000 gefahrenen Kilometern, dann ist der Wert des Gebrauchtwagens 7.115,10 EUR.
Dieses Modell hat eine Allgemeingültigkeit. Wir können beliebige Werte eintragen und erhalten einen vorhergesagten Wert.
Prüfen der Signifikanzwerte
Im nächsten Schritt prüfen wir die Signifikanz der Koeffizienten. In der Tabelle Koeffizienten blicken wir deshalb auf die Spalte “Sig.” und sehen die p-WerteP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist..
In unserem Beispiel sind alle Prädiktoren signifikant.
Mein Modell ist signifikant, einzelne Koeffizienten nicht. Was tun?
Das kann an der Multikollinearität liegen, über die wir weiter oben berichtet haben. Ein weiterer Grund sind zu viele Prädiktoren in der Gleichung haben. Wenn es zu viele Prädiktoren oder Fälle (Cases) gibt, kann der Signifikanztest verzerrt werden. In diesem Fall solltest du die nicht signifikante Variable ausschließen und das Modell erneut berechnen.
Effektstärken berechnen
Um die Effektstärken zu berechnen, gibt es einen hervorragenden Rechner auf statistikguru.de
Ergebnisse publizieren
Eine Autokorrelation in den Residuen lag nicht vor, da die Durbin-Watson-Statistik einen Wert von 1.622 aufweist.
Das Regressionsmodell zeigt einen R² = 0.555 (korrigertes R² = 0.550) und ist signifikant p<0.001 (α ≤ 0.5).
Die Prädiktoren Kilometerstand, PS und Registrierungsdatum sagen statistisch signifikant das Kriterium Preis eines Gebrauchtwagens voraus. Die Regressionsgleichung lautet Preis = 221.00 * Registrierungsdatum + 89.95 * PS + 0.07 * Kilometerstand – 439,666.56.
Tipp beim Publizieren
Es kommt häufig vor, dass nicht nur eine Regressionsgleichung gerechnet wird und mehrere HypothesenHypothese Eine Hypothese ist eine vorläufige Annahme über einen Zusammenhang oder ein Phänomen, die aufgrund von Beobachtungen oder vorherigen Erkenntnissen gemacht wird und überprüft werden kann, indem sie durch Forschung oder Experimente gestützt oder widerlegt wird. geprüft werden. In diesem Fall kann es sinnvoll sein, die Daten als Tabelle darzustellen. Jede weitere Gleichung kommt in eine neue Zeile.
| HypotheseHypothese Eine Hypothese ist eine vorläufige Annahme über einen Zusammenhang oder ein Phänomen, die aufgrund von Beobachtungen oder vorherigen Erkenntnissen gemacht wird und überprüft werden kann, indem sie durch Forschung oder Experimente gestützt oder widerlegt wird. | Regressionsgleichung | R² | Adj. R² | Sig. | DWS |
|---|---|---|---|---|---|
| H1 | Preis = 221.00 * Registrierungsdatum + 89.95 * PS + 0.07 * Kilometerstand – 439,666.56. | .555 | .550 | .001*** | 1.622 |
=p ≤ .05, ** = p ≤ .01, *** = p ≤ .001.
Häufig gestellte Fragen und Antworten: Multiple lineare Regression
Wann wird eine multiple lineare Regression verwendet?
Eine multiple lineare Regression wird verwendet, wenn es darum geht, den Einfluss von mehreren unabhängigen Variablen auf eine abhängige Variable zu schätzen und vorherzusagen, wie sich die abhängige Variable aufgrund von Änderungen in den unabhängigen Variablen ändern wird.
Die multiple lineare Regression ist ein mächtiges Analysewerkzeug, das in vielen Bereichen der Wissenschaft, des Geschäfts und anderer Felder eingesetzt wird, um z.B. zu untersuchen, wie sich Alter, Geschlecht und Bildungsniveau auf das Einkommen einer Person auswirken, oder um zu bestimmen, wie sich verschiedene Marketingfaktoren auf den Verkauf eines Produkts auswirken.
Es ist wichtig zu beachten, dass die multiple lineare Regression nur gültig ist, wenn die Annahmen der linearen Regression erfüllt sind, wie z.B. lineare Beziehung zwischen den Variablen und Normalverteilung der Residuen. Wenn diese Annahmen nicht erfüllt sind, können andere Analysemethoden wie z.B. die nicht-lineare Regression oder die multivariate Regression in Betracht gezogen werden.
Was ist der Unterschied zwischen einer linearen und multiplen Regression?
Der Unterschied zwischen einer linearen Regression und einer multiplen Regression besteht darin, dass die lineare Regression nur eine unabhängige Variable (auch Prädiktor genannt) verwendet, um den Einfluss auf die abhängige Variable (auch Zielvariable genannt) zu schätzen, während die multiple Regression mehrere unabhängige Variablen verwendet.
In der linearen Regression wird eine lineare Beziehung zwischen der abhängigen Variable und der unabhängigen Variable geschätzt, während in der multiplen Regression eine lineare Beziehung zwischen der abhängigen Variable und jeder der unabhängigen Variablen geschätzt wird.
Die lineare Regression ist in vielen Fällen ein mächtiges Analysewerkzeug, aber es gibt Fälle, in denen mehrere Variablen in Betracht gezogen werden müssen, um ein umfassenderes Verständnis der Beziehungen zwischen den Variablen zu erhalten. In solchen Fällen kann die multiple Regression eine geeignete Analysemethode sein.
Es ist wichtig zu beachten, dass die multiple Regression nur gültig ist, wenn die Annahmen der linearen Regression erfüllt sind, wie z.B. lineare Beziehung zwischen den Variablen und Normalverteilung der Residuen. Wenn diese Annahmen nicht erfüllt sind, können andere Analysemethoden wie z.B. die nicht-lineare Regression oder die multivariate Regression in Betracht gezogen werden.
Welche Arten von Regressionen gibt es?
Es gibt verschiedene Arten von Regressionen, die je nach der Art der abhängigen und unabhängigen Variablen und der Form der Beziehung zwischen ihnen verwendet werden. Hier sind einige Beispiele für verschiedene Arten von Regressionen:
– Lineare Regression: Die lineare Regression wird verwendet, um die lineare Beziehung zwischen einer abhängigen und einer unabhängigen Variablen zu beschreiben. Das Modell besteht aus einer geraden Regressionslinie, die die Beziehung zwischen den Variablen darstellt.
– Multiple lineare Regression: Die multiple lineare Regression wird verwendet, wenn es mehrere unabhängige Variablen gibt, die die abhängige Variable erklären sollen.
– Polynomiale Regression: Die polynomiale Regression wird verwendet, wenn die Beziehung zwischen den Variablen durch eine Kurve und nicht durch eine gerade Linie beschrieben werden kann.
– Logistische Regression: Die logistische Regression wird verwendet, wenn die abhängige Variable binär ist, das heißt, sie kann nur zwei mögliche Werte annehmen (z.B. „ja“ oder „nein“). Sie wird häufig verwendet, um Vorhersagen über die Wahrscheinlichkeit von Ereignissen zu treffen.
Es gibt noch weitere Regressionen wie die multinominale Regression, auf die wir hier nicht weiter eingehen möchten.
Was bedeutet R2 bei Regressionen?
Der R2 (auch bekannt als „R²“, „Koeffizient der Determinations-Koeffizient“) ist ein Maß dafür, wie gut ein Regressionsmodell die Variabilität der abhängigen Variable erklärt. Er wird berechnet, indem man den Anteil der Varianz der abhängigen Variable, der durch das Regressionsmodell erklärt wird, durch die Gesamtvarianz der abhängigen Variable teilt.
Der R2 nimmt Werte zwischen 0 und 1 an, wobei ein höherer Wert bedeutet, dass das Regressionsmodell eine bessere Erklärung der Variabilität der abhängigen Variable liefert. Ein R2-Wert von 0 bedeutet, dass das Regressionsmodell keine Erklärung für die Variabilität der abhängigen Variable liefert, während ein R2-Wert von 1 bedeutet, dass das Regressionsmodell die Variabilität der abhängigen Variable vollständig erklärt.
Es ist wichtig zu beachten, dass der R2 nicht immer ein zuverlässiges Maß für die Vorhersagegenauigkeit eines Regressionsmodells ist, insbesondere wenn das Modell auf neuen Daten getestet wird.
Weitere Ressourcen für multiple lineare Regression
Wie viele Beobachtungen braucht man für eine Regression?
Es gibt keine feste Regel, wie viele Beobachtungen man für eine Regression benötigt. Die Anzahl der Beobachtungen, die benötigt werden, hängt von verschiedenen Faktoren ab, wie der Anzahl der unabhängigen Variablen, der Komplexität des Regressionsmodells und der Stärke der Beziehung zwischen den Variablen.
In der Regel sollte man jedoch genügend Beobachtungen haben, um ein repräsentatives Muster der Daten zu erhalten und um sicherzustellen, dass das Modell ausreichend gut an die Daten angepasst wird. Als allgemeine Regel gilt, dass man für jede unabhängige Variable, die man ins Modell einführt, mindestens 10 Beobachtungen haben sollte. Wenn das Modell jedoch sehr komplex ist oder wenn die Beziehung zwischen den Variablen sehr schwach ist, könnten mehr Beobachtungen erforderlich sein.
Es ist wichtig zu beachten, dass man nicht immer so viele Beobachtungen wie möglich haben sollte. In manchen Fällen könnte es sinnvoller sein, weniger Beobachtungen zu haben, aber diese sorgfältig auszuwählen, um sicherzustellen, dass sie relevant und repräsentativ für die Population sind, auf die man sich beziehen möchte.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn