Die Pearson-Produkt-Moment-KorrelationKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird., auch einfach Pearson-Korrelation genannt, ist ein statistisches Maß für die Stärke und Art der linearen Beziehung zwischen zwei Variablen. Sie wird verwendet, um festzustellen, wie stark eine Änderung in einer Variablen mit einer Änderung in einer anderen Variablen korreliert ist. In diesem Beitrag werden wir uns näher mit der Berechnung und Interpretation der Pearson-Korrelation befassen.
Was wird mit der Pearson-Produkt-Moment-Korrelation berechnet?
Die Pearson-Produkt-Moment-Korrelation berechnet die Stärke und Art des linearen Zusammenhangs zwischen zwei Variablen. Sie wird als Wert zwischen -1 und 1 ausgedrückt, wobei -1 eine perfekte negative Korrelation, 0 keine Korrelation und 1 eine perfekte positive Korrelation bedeutet. Ein Wert von 1 bedeutet, dass zwischen den beiden Variablen eine perfekte positive lineare Beziehung besteht, d. h. wenn die Werte einer Variablen steigen, steigen auch die Werte der anderen Variablen und umgekehrt. Ein Wert von -1 bedeutet, dass eine perfekte negative lineare Beziehung besteht, d. h. wenn die Werte einer Variablen steigen, sinken die Werte der anderen Variablen und umgekehrt. Ein Wert von 0 bedeutet, dass keine lineare Beziehung zwischen den beiden Variablen besteht.
Es ist wichtig zu beachten, dass die Pearson-Korrelation nur die lineare Beziehung zwischen Variablen misst und nicht die KausalitätKausalität Kausalität bezieht sich auf den Zusammenhang zwischen zwei oder mehr Ereignissen oder Variablen, bei dem ein Ereignis oder eine Variable (die Ursache) das andere Ereignis oder die andere Variable (die Wirkung) verursacht..
Unterschied zwischen Kausalität und Korrelation
Eines der Hauptprobleme bei der Verwendung der Pearson-Produkt-Moment-Korrelation besteht darin, dass eine Korrelation zwischen zwei Variablen nicht bedeutet, dass eine dieser Variablen die andere verursacht. Dies ist als “Korrelation ist nicht Kausalität”-Problem bekannt. Eine Korrelation beschreibt lediglich eine statistische Beziehung zwischen zwei Variablen, und es gibt viele Gründe, warum diese Beziehung bestehen kann, die nichts mit Kausalität zu tun haben. Zum Beispiel kann eine dritte Variable die beiden Variablen beeinflussen und so eine Korrelation verursachen. Es ist daher wichtig, bei der Interpretation der Ergebnisse vorsichtig zu sein und weitere Untersuchungen durchzuführen, um die Kausalität zu bestätigen oder auszuschließen.
Wann wird die Pearson-Produkt-Moment Korrelation verwendet?
Die Pearson-Produkt-Moment-Korrelation wird in der Statistik verwendet, um die Stärke und Art einer linearen Beziehung zwischen zwei Variablen zu bestimmen. Sie wird häufig in verschiedenen Anwendungen verwendet, z. B:
- In der medizinischen Forschung, um zu untersuchen, ob eine Beziehung zwischen verschiedenen Gesundheitsindikatoren wie Blutdruck und Cholesterinspiegel besteht.
- In der Psychologie, um den Zusammenhang zwischen verschiedenen Persönlichkeitsmerkmalen und Verhaltensweisen zu untersuchen. Zum Beispiel kann die Korrelation zwischen Neurotizismus und Depression untersucht werden.
- In den Wirtschaftswissenschaften, um den Zusammenhang zwischen verschiedenen Finanzindikatoren wie Aktienkursen und Wirtschaftswachstum zu untersuchen.
- In den Sozialwissenschaften, um den Zusammenhang zwischen Bildung und Einkommen zu untersuchen.
- In den Umweltwissenschaften, um den Zusammenhang zwischen verschiedenen Umweltfaktoren wie Luftqualität und Gesundheit zu untersuchen.
Vorrausetzungen
- SkalenniveauSkalenniveau Das Skalenniveau bezieht sich auf den Typ von Daten, der in einer Studie erhoben wurde, und gibt an, wie die Daten in Bezug auf die Messbarkeit und die Möglichkeit zur Verwendung von Statistiken kodifiziert sind.: Beide Variablen müssen mindestens intervallskaliert sein. Wenn eine Variable mindestens ordinalskaliert ist, sollte der Spearman-Korrelationskoeffizient verwendet werden. Mehr zu Skalenniveaus.
- LinearitätLinearität Linearität bezieht sich auf die Beziehung zwischen zwei oder mehr Variablen, die durch eine gerade Linie dargestellt wird, bei der die Veränderung einer Variablen direkt proportional zur Veränderung der anderen Variable ist. : Die beiden Variablen sollten in einer möglichst linearen Beziehung zueinander stehen. Andernfalls neigt der Pearson-Korrelationskoeffizient nach Pearson dazu, den Zusammenhang zu unterschätzen. Lesen Sie mehr über Linearität in SPSS messen.
- AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind.: Der Datensatz sollte möglichst frei von Ausreißern sein. Mit diesem Verfahren können Ausreißer im Datensatz identifiziert werden.
- Varianz und KovarianzKovarianz Die Kovarianz ist ein Maß für den Zusammenhang zwischen zwei oder mehr Variablen, das angibt, wie sehr sich die Werte der Variablen im Verhältnis zueinander ändern und kann verwendet werden, um die Streuung der Daten zu beschreiben.: Beide Variablen sollten keine endliche Varianz und Kovarianz aufweisen. Erfahre mehr über Kovarianz.
Pearson-Produkt-Moment Korrelation in SPSS berechnen
Auswahl im Menü

Im Menü klicken wir oben auf Analysieren > Korrelation > Bivariat
Variablen zuordnen

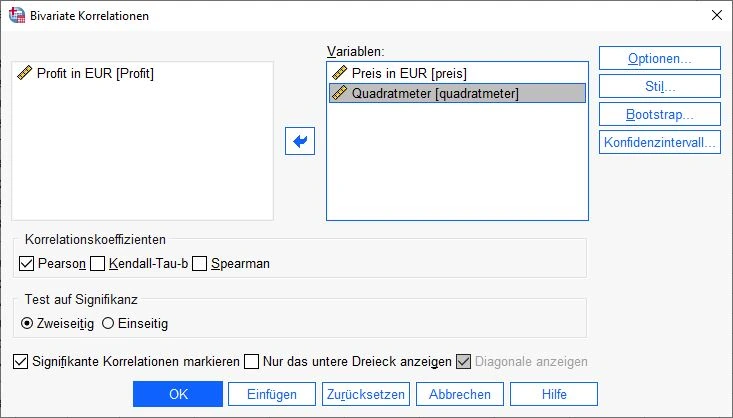
Ein Dialogfenster erscheint. Im linken Feld sind alle verfügbaren Variablen unseres Datensatzes aufgelistet. Auf der rechten Seite befindet sich ein Feld mit der Überschrift Variablen. Hierher ziehen wir alle Variablen, die wir untersuchen wollen.
Unterhalb der Felder haben wir mehrere Optionen für die Berechnung der KorrelationenKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird.. Wir kreuzen Pearson an.
Der Test auf Signifikanz ist normalerweise zweiseitig.
Wir setzen ein Häkchen bei Signifikante Korrelationen markieren. Dies ist sehr hilfreich bei großen Tabellen mit vielen Variablen.In unserem Beispiel sind das die Variablen Preis in EUR und Quadratmeter.
Dann klicken wir auf die Schaltfläche Optionen auf der rechten Seite.
Optionen auswählen

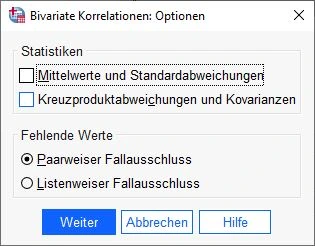
Das Fenster Optionen für bivariate Korrelationen erscheint. Hier vergewissern wir uns, dass keine Statistik ausgewählt ist (da wir sie nicht benötigen).
Außerdem sollte die Option “Paarweiser Fallausschluss” für fehlende Werte ausgewählt werden.
Wir bestätigen unsere Eingaben mit einem Klick auf den Weiter-Button.
Bereit zu starten

Wir sind fertig und klicken auf OK. Die Berechnungen beginnen. Die Ergebnisse werden in der Ausgabedatei von SPSS angezeigt.
Analyse der Pearson-Produkt-Moment-Korrelation in SPSS
Korrelationskoeffizient nach Pearson bestimmen
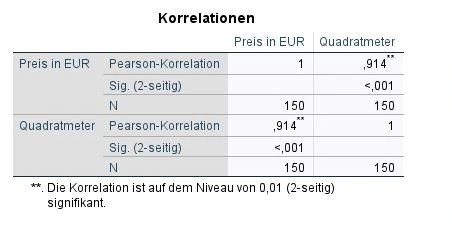
In der Ausgabedatei von SPSS erscheint eine Tabelle mit dem Namen Korrelationen. Diese Tabelle stellt unsere beiden Variablen gegenüber. Die Ergebnisse sind also gespiegelt.
Wir schauen uns die erste Zeile und den Wert der Pearson-Korrelation an. Wir sehen, dass der Korrelationskoeffizient r=.914 hoch ist. Das ist ein sehr hoher Wert.
Als zweites schauen wir uns die Signifikanz an, um zu überprüfen, ob die Ergebnisse zufällig sind oder nicht. Dazu sehen wir uns die Zeile Signifikanz (Sig.) an. Sie gibt uns den p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. an. In unserem Beispiel sehen wir eine Signifikanz von p <.001. Wir vergleichen das Ergebnis mit dem Signifikanzniveausignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist..
N beschreibt den Stichprobenumfang, der für die Berechnung verwendet wurde. In unserem Beispiel wurden keine Fälle ausgeschlossen.
Was ist das Signifikanzniveau und der p-Wert?
Das Signifikanzniveau in der Statistik gibt an, mit welcher Wahrscheinlichkeit ein bestimmtes Ergebnis zufällig auftritt, wenn tatsächlich kein Effekt vorliegt. Es wird in der Regel als Alpha-Wert (α) angegeben und liegt in der Regel bei 0,05 oder 0,01. Der Alpha-Wert gibt die Wahrscheinlichkeit an, dass ein Fehler vom Typ I (falsch-positive Entscheidung) gemacht wird, wenn tatsächlich kein Effekt vorliegt.
Der p-Wert ist ein statistisches Maß, das die Wahrscheinlichkeit angibt, dass ein bestimmtes Ergebnis oder eine größere Abweichung von Null zufällig auftritt. Ist der p-Wert kleiner als das vorher festgelegte Signifikanzniveau (α), wird das Ergebnis als signifikant angesehen. Das bedeutet, dass es unwahrscheinlich ist, dass das Ergebnis zufällig auftritt und dass wahrscheinlich ein echter Effekt vorliegt. Ist der p-Wert größer als das Signifikanzniveau, wird das Ergebnis als nicht signifikant angesehen und es wird kein Effekt vermutet.
Signifikanzen können nicht 0 oder 1 sein, sondern immer dazwischen liegen. In diesem Fall würde der Wert wie folgt angegeben werden: p<.001
Was sind positive und negative Korrelationen?
Der Unterschied zwischen einer positiven und einer negativen Korrelation besteht darin, wie sich die Werte der beiden Variablen gemeinsam verändern.
Eine positive Korrelation bedeutet, dass sich die Werte der beiden Variablen tendenziell in die gleiche Richtung verändern. Wenn eine Variable zunimmt, nimmt auch die andere Variable zu und umgekehrt. Ein Beispiel wäre die Korrelation zwischen Alter und Berufserfahrung: Je älter man ist, desto mehr Berufserfahrung hat man.
Eine negative Korrelation bedeutet, dass sich die Werte der beiden Variablen tendenziell in entgegengesetzte Richtungen entwickeln. Wenn eine Variable steigt, sinkt die andere und umgekehrt. Ein Beispiel hierfür wäre die Korrelation zwischen Alter und Körpertemperatur: Je älter man wird, desto niedriger ist die Körpertemperatur.
Ergebnisse interpretieren
Der Korrelationskoeffizient nach Pearson ist leicht zu interpretieren. Dazu wird die folgende Tabelle nach Cohen (1988) herangezogen
| Wert des Korrelationskoeffizienten | Interpretation |
|---|---|
| |r| = .10 | schwach (gering) |
| |r| = .30 | moderat (mittlere) |
| |r| = .50 | stark (groß) |
Ergebnisse publizieren
Es konnte eine starke Korrelation zwischen den Variablen Preis in EUR und Quadratmetern festgestellt werden, r=.914, p<.001
5 Fakten über die Pearson-Produkt-Moment Korrelation
- Die Pearson-Produkt-Moment-Korrelation berechnet die Stärke und Art der linearen Beziehung zwischen zwei Variablen.
- Der Wert der Korrelation liegt immer zwischen -1 und 1, wobei -1 eine perfekte negative Korrelation, 0 keine Korrelation und 1 eine perfekte positive Korrelation bedeutet.
- Eine Korrelation von 1 oder -1 bedeutet, dass zwischen den beiden Variablen eine perfekte lineare Beziehung besteht, während eine Korrelation von 0 bedeutet, dass keine lineare Beziehung besteht.
- Es ist zu beachten, dass die Pearson-Korrelation nur die lineare Beziehung zwischen Variablen misst und nicht die Kausalität.
- Die Pearson-Korrelation kann nur verwendet werden, wenn die Daten normalverteilt sind; andernfalls sollten andere Methoden wie die Kendall-Korrelation oder die Spearman-Korrelation verwendet werden.
Häufig gestellte Fragen und Antworten: Pearson-Produkt-Moment Korrelation
Was sagt die Pearson Korrelation aus?
Die Pearson-Korrelation ist ein statistisches Maß, das den linearen Zusammenhang zwischen zwei Variablen misst. Der Wert der Korrelation liegt zwischen -1 und 1, wobei -1 eine perfekte negative Korrelation, 0 keine Korrelation und 1 eine perfekte positive Korrelation bedeutet. Eine positive Korrelation bedeutet, dass sich die beiden Variablen tendenziell in die gleiche Richtung zueinander bewegen, während eine negative Korrelation bedeutet, dass sich die beiden Variablen tendenziell in entgegengesetzte Richtungen bewegen. Eine Korrelation von 1 oder -1 bedeutet, dass eine perfekte lineare Beziehung zwischen den beiden Variablen besteht, während eine Korrelation von 0 bedeutet, dass keine lineare Beziehung besteht. Es ist zu beachten, dass die Pearson-Korrelation nur die lineare Beziehung zwischen den Variablen misst und nicht die Kausalität.
Wann ist eine Pearson Korrelation signifikant?
Eine Pearson-Korrelation gilt als signifikant, wenn der p-Wert kleiner als das vorgegebene Signifikanzniveau (α) ist. Das Signifikanzniveau wird in der Regel auf 0,05 oder 0,01 festgelegt und gibt die Wahrscheinlichkeit an, mit der ein Fehler vom Typ I (falsch-positive Entscheidung) gemacht wird, wenn tatsächlich keine Korrelation vorliegt. Wenn der p-Wert kleiner als das Signifikanzniveau ist, bedeutet dies, dass die Korrelation unwahrscheinlich ist und wahrscheinlich eine echte Korrelation zwischen den beiden Variablen besteht.
Es ist zu beachten, dass die Signifikanz der Korrelation auch von der Größe der Stichprobe beeinflusst wird: je größer die Stichprobe, desto geringer die Wahrscheinlichkeit eines Fehlers.
Wann wird die Produkt-Moment-Korrelation verwendet?
Die Produkt-Moment-Korrelation, auch Pearson-Korrelation genannt, wird verwendet, um die lineare Beziehung zwischen zwei skalaren Variablen zu messen. Sie wird hauptsächlich verwendet, um die Stärke und Richtung einer linearen Beziehung zwischen zwei Variablen zu bestimmen. Sie wird verwendet, wenn die Daten normal verteilt sind und die Beziehung zwischen den Variablen annähernd linear ist. Er kann verwendet werden, um die Beziehung zwischen zwei kontinuierlichen Variablen, wie Alter und Gewicht, oder zwei diskreten Variablen, wie Geschlecht und Rauchgewohnheiten, zu messen. Es ist auch ein nützliches Werkzeug in der statistischen Datenanalyse, um die Beziehung zwischen verschiedenen Variablen zu untersuchen und zu verstehen.
Was sagt Korrelation aus?
Die Korrelation ist ein statistisches Maß, das die Beziehung zwischen zwei oder mehr Variablen beschreibt. Es gibt verschiedene Arten von Korrelationen, z. B. die Pearson-Korrelation, die die lineare Beziehung zwischen zwei skalaren Variablen misst, oder die Spearman-Korrelation, die die monotone Beziehung zwischen zwei skalaren Variablen misst.
Eine Korrelation gibt das Ausmaß und die Richtung der Beziehung zwischen den Werten der beiden Variablen an.
Eine positive Korrelation bedeutet, dass sich die beiden Variablen tendenziell in dieselbe Richtung zueinander bewegen, während eine negative Korrelation bedeutet, dass sich die beiden Variablen tendenziell in entgegengesetzte Richtungen zueinander bewegen. Eine Korrelation von 0 bedeutet, dass keine Beziehung zwischen den beiden Variablen besteht. Es ist wichtig zu beachten, dass die Korrelation keine Kausalität impliziert und dass andere Faktoren die Beziehung beeinflussen können.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn