Was ist eine ANOVA mit Messwiederholung?
Eine ANOVA mit Messwiederholung wird verwendet, um zu überprüfen, ob es signifikante Unterschiede zwischen den Mittelwerten von zwei oder mehr Gruppen gibt, wenn die Daten durch Zeit, Personen oder andere Faktoren wiederholt gemessen wurden. Diese Art der Analyse ist besonders nützlich, wenn man mehrere Messungen für jede Beobachtung hat und überprüfen möchte, ob es signifikante Unterschiede in den Mittelwerten dieser Messungen gibt. In diesem Artikel wird beschrieben, wie man eine ANOVA mit Messwiederholung in SPSS durchführt und wie man das Ergebnis interpretiert. Zunächst wird jedoch eine kurze Einführung in die Konzepte der ANOVA mit Messwiederholung gegeben.
ANOVA mit Messwiederholung, auch als „ANOVA mit ungepaarten Stichproben“ oder „einfaktorielle ANOVA mit Messwiederholung“ bezeichnet, ist ein statistisches Verfahren, das verwendet wird, um zu überprüfen, ob es signifikante Unterschiede zwischen den Mittelwerten von zwei oder mehr Gruppen gibt. Die ANOVA mit Messwiederholung ist eine Erweiterung der Einfaktorielle ANOVA, die verwendet wird, wenn es nur eine unabhängige Variable gibt, aber mehrere Messungen für jede Beobachtung gemacht wurden. Die ANOVA mit Messwiederholung testet die HypotheseHypothese Eine Hypothese ist eine vorläufige Annahme über einen Zusammenhang oder ein Phänomen, die aufgrund von Beobachtungen oder vorherigen Erkenntnissen gemacht wird und überprüft werden kann, indem sie durch Forschung oder Experimente gestützt oder widerlegt wird., dass die Mittelwerte aller Gruppen gleich sind, indem sie die Varianz innerhalb der Gruppen und die Varianz zwischen den Gruppen misst. Wenn die Varianz zwischen den Gruppen größer ist als die Varianz innerhalb der Gruppen, gibt es wahrscheinlich signifikante Unterschiede zwischen den Mittelwerten der Gruppen.
Was berechnet die ANOVA mit Messwiederholung?
Die ANOVA mit Messwiederholung berechnet zwei Arten von Varianz: die Varianz innerhalb der Gruppen und die Varianz zwischen den Gruppen. Die Varianz innerhalb der Gruppen misst die Streuung der Werte innerhalb einer Gruppe und gibt an, wie sehr sich die Werte innerhalb einer Gruppe voneinander unterscheiden. Die Varianz zwischen den Gruppen misst die Streuung der Mittelwerte der Gruppen und gibt an, wie sehr sich die Mittelwerte der Gruppen voneinander unterscheiden.
Die ANOVA mit Messwiederholung verwendet diese beiden Arten von Varianz, um zu überprüfen, ob es signifikante Unterschiede zwischen den Mittelwerten der Gruppen gibt. Wenn die Varianz zwischen den Gruppen größer ist als die Varianz innerhalb der Gruppen, gibt es wahrscheinlich signifikante Unterschiede zwischen den Mittelwerten der Gruppen. Wenn die Varianz innerhalb der Gruppen größer ist als die Varianz zwischen den Gruppen, gibt es keine signifikanten Unterschiede zwischen den Mittelwerten der Gruppen. Die ANOVA mit Messwiederholung berechnet auch einen F-Wert, der verwendet wird, um die Signifikanz des Unterschieds zu beurteilen.
Unser Beispiel: Wie wächst der Umsatz in unseren Filialen?
Unser Beispieldatensatz vergleicht die Umsätze von mehreren Tausend Filialen in Deutschland von einer großen fiktiven Restaurantkette. Die Umsätze werden in 4 Zeitabständen gemessen. Nehmen wir an, es sind 4 Jahre. Als Statistiker möchten wir nun untersuchen, ob es Schwankungen im Umsatz gab und ob die Umsatzentwicklung signifikant war.
Wo kann ich die Beispieldaten herunterladen?
Die Beispieldaten findest du hier: Beispieldaten
Voraussetzungen
- Die abhängige Variableabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. ist intervallskaliert. Die ANOVA verwendet aufwändige Rechnungen, für die wir ein entsprechendes SkalenniveauSkalenniveau Das Skalenniveau bezieht sich auf den Typ von Daten, der in einer Studie erhoben wurde, und gibt an, wie die Daten in Bezug auf die Messbarkeit und die Möglichkeit zur Verwendung von Statistiken kodifiziert sind. benötigen (Intervall oder Ratio). Hier ist die Anleitung für Skalenniveaus.
- Innensubjektfaktor ist nominalskaliert. Der Innensubjektfaktor ist die Variable, die die Gruppen voneinander trennt. Beispielsweise die Form der Diät, die Stadt, etc. Diese Variable muss nominalskaliert sein und mindestens drei Gruppen haben. Falls du weniger als drei Gruppen hast, kannst du den t-Test für abhängige Stichproben verwenden.
- Unabhängige Messungenunabhängige Messungen Unabhängige Messungen sind Messungen, die von verschiedenen Beobachtern oder Messverfahren durchgeführt werden und die vermutlich keine Wechselwirkungen oder Verzerrungen durch die Beobachter oder Messverfahren haben. Sie werden verwendet, um die Zuverlässigkeit und Validität von Messungen und Studien zu verbessern und werden häufig in der Psychologie und Sozialwissenschaften verwendet.: die Varianzanalyse vergleicht unterschiedliche Messobjekte, in unserem Fall Versuchspersonen, zu unterschiedlichen Zeitpunkten. Die Gruppen oder Bedingungen (UV) dürfen sich nicht gegenseitig beeinflussen, das heißt, eine Versuchsperson darf sich unter keinen Umständen in mehreren Gruppen zu befinden.
- AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind.: Die ANOVA ist empfindlich gegenüber Ausreißern, weshalb der Datensatz auf Ausreißer hin überprüft werden sollte. Bestenfalls gibt es keine Ausreißer in keiner Gruppe. Anleitung für Ausreißer.
- NormalverteilungNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. : die abhängige Variable (Gewicht) in jeder Gruppe sollte so weit wie möglich normalverteilt sein – jedoch nicht zwangsläufig. Das gilt für jede unserer untersuchten Gruppen. Anleitung Test auf Normalverteilung.
- Sphärizität: Die Varianzen zwischen den einzelnen Gruppen sollte gleich sein. Falls die Sphärizität nicht gegeben ist, besteht die Gefahr für einen Fehler 1. Art (α-Fehler, falsch positiv). Das bedeutet, dass wir ein Ergebnis bestätigen, obwohl es nicht wahr. (Ein Patient wird als krank angesehen, obwohl er gesund ist.)
Berechnung ANOVA mit Messwiederholung in SPSS
Berechnung ANOVA mit Messwiederholung in SPSS
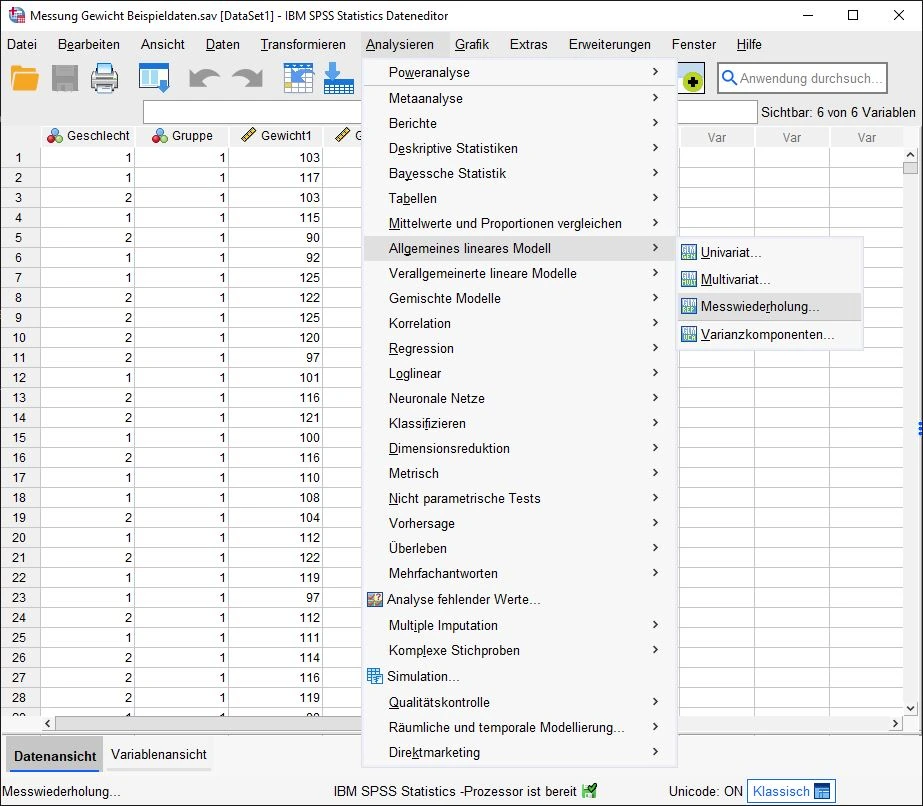
Auswahl Menü

Wir wählen aus: Analysieren > Allgemeines lineares Modell > Messwiederholung.
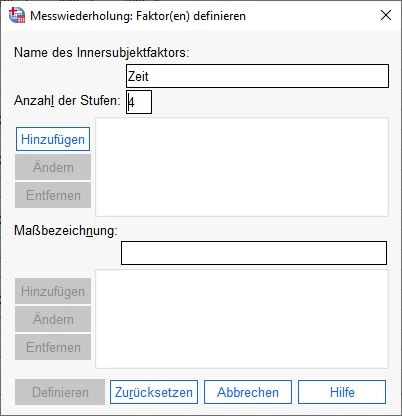
Faktoren einstellen

Im nächsten Schritt geben wir die Anzahl der Stufen des Innersubjektfaktors an. Konkret geht es bei Messwiederholung darum, etwas Wiederkehrendes zu messen. In unserem Fall ist es die Zeit.
Wir haben in unserem Datensatz 4 Messungen, deshalb ist die Anzahl der Stufen 4.
Wir geben beide Werte ein und klicken auf Hinzufügen.
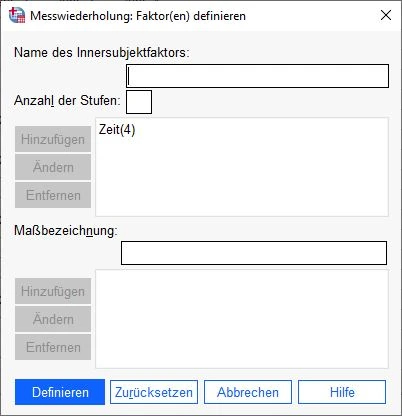
Faktoren definieren

Im oberen Feld sehen wir nun die Eingabe Zeit(4). Die Eingaben wurden korrekt übernommen.
Im nächsten Schritt klicken wir unten auf den Knopf Definieren., um die Werte zu übernehmen.
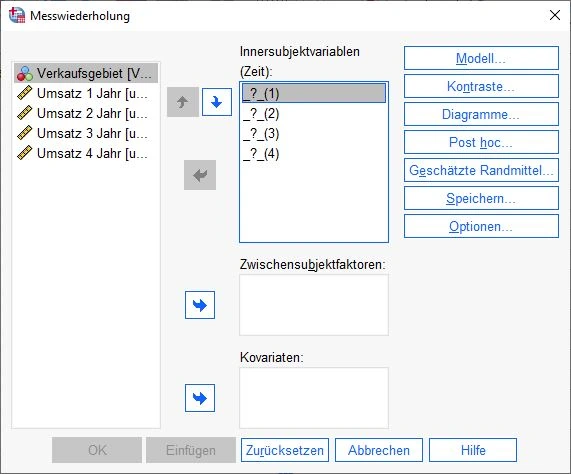
Auswahl der Variablen

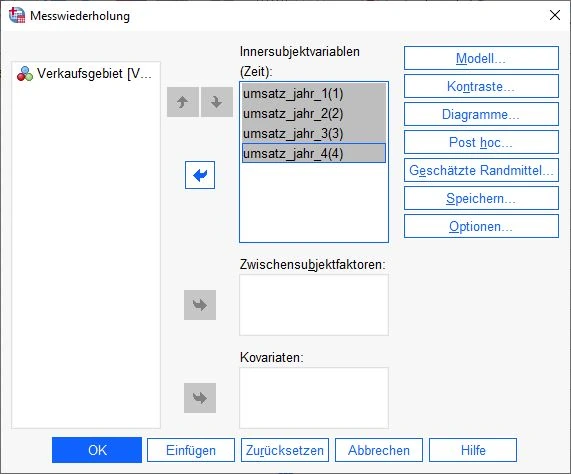
Nun sehen wir ein wichtiges Dialogfenster. Hier sehen wir unsere Variablen aus dem Datensatz auf der linken Seite. Wir ziehen die notwendigen Variablen auf das Feld Innersubjektvariablen. SPSS möchte 4 Variablen haben, weil wir im Schritt vorher 4 Stufen ausgewählt haben.
Deshalb ziehen wir die vier Variablen Umsatz 1 Jahr, Umsatz 2 Jahr, Umsatz 3 Jahr und Umsatz 4 Jahr auf die entsprechenden Platzhalter. Wenn alles geklappt hat, sieht unser Fenster so aus wie im nächsten Bildschirmausschnitt.
Auswahl Diagramme

Die Innersubjektfaktoren sind vollständig belegt, prima. Im nächsten Schritt klicken wir auf der rechten Seite des Dialogfensters auf die Option Diagramme.
Hinweis: In unserem Datensatz gibt es noch die nominal skalierte Variable Verkaufsgebiet. Im Grunde könnten wir mit diesem Datensatz zusätzlich die Information des Verkaufsgebietes (Nord, Ost, West und Süd) in die Berechnung mitaufnehmen. Dann haben wir eine sogenannte mixed ANOVA. Mehr Informationen gibt es in dieser Anleitung für mixed ANOVA.Auswahl Diagramme

In dem Dialogfenster Messwiederholung: Profilplots stellen wir uns Diagramme zusammen. In diesem Schritt wählen wir den Faktor Zeit und schieben diesen auf das Feld Horizontale Achse. Anschließend klicken wir auf den Knopf Hinzufügen.
Diagramme einstellen: Profilplots

Nun befindet sich der Faktor Zeit im mittleren Feld.
Mehr müssen wir nicht einstellen. Wir klicken auf Weiter.
Menü Messwiederholung

Jetzt wählen wir auf der rechten Seite die Option Geschätzte Randmittel.
Dialogfenster: Geschätzte Randmittel

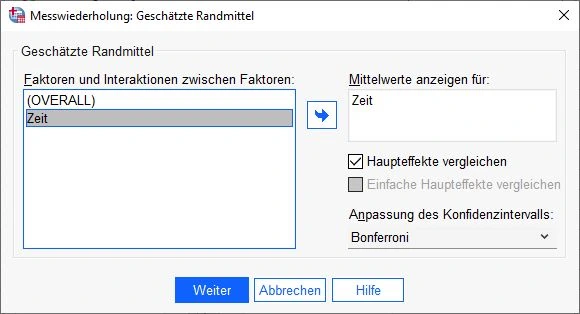
In diesem Dialogfenster klicken wir auf den Faktor auf der linken Seite und bringen diesen in das Feld Mittelwerte anzeigen für. Wir stellen sicher, dass ein Haken auf Haupteffekte vergleichen gesetzt ist und klicken auf Weiter.
Hinweis: Zu Beginn der Anleitung haben wir nur einen Faktor Zeit erstellt. Aus diesem Grund sehen wir nur diesen einen Faktor.
Optionen im Menü auswählen

Wir klicken in der rechten Seite auf Optionen.
Dialogfenster: Optionen

In diesem Dialogfenster wählen wir folgende Optionen aus:
– Deskriptive Statistiken
– Schätzungen der EffektgrößeAnschließend klicken wir auf Weiter.
ANOVA mit Messwiederholung in SPSS starten

Wir sind bereit und klicken auf den OK-Knopf weiter unten.
Analyse der Ergebnisse: ANOVA mit Messwiederholung in SPSS
Deskriptive Statistik
Wir beginnen unsere Analyse mit der Tabelle Deskriptive Statistiken.
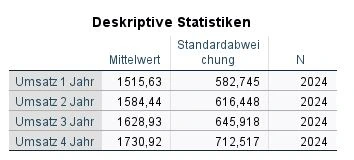
Für alle vier Messzeitpunkte (Stufe des Innersubjektfaktors) wird der Mittelwert (M), die StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. (SD) und die Anzahl der gemessenen Fälle (N) angezeigt.
Mauchly Test
In der SPSS-Ausgabe finden wir die Tabelle „Mauchly-Test auf Sphärizität“. Besonders wichtig ist die Spalte „Sig.“.
Wenn der Wert in dieser Spalte kleiner als 0,05 ist, müssen wir ein Korrekturverfahren anwenden. Aber keine Sorge, SPSS bietet uns drei verschiedene Verfahren zur Auswahl: Greenhouse-Geisser, Huynh-Feldt und Untergrenze. Diese Verfahren sind in den rechten Spalten der Tabelle aufgeführt.
Sphärizität erklärt
In der Statistik ist die Annahme der „Sphärizität“ besonders wichtig für eine Methode, die „Mixed ANOVA“ genannt wird. Diese Methode geht davon aus, dass bei einer wiederholten Messung mit mehr als zwei Durchgängen alle Unterschiede zwischen den unabhängigen Variablen gleich sein sollten. Dies wird auch als „HomoskedastizitätHomoskedastizität Homoskedastizität bezieht sich auf die Gleichmäßigkeit der Varianz der Residuen in einem statistischen Modell und bedeutet, dass die Varianz der Residuen über alle Werte der unabhängigen Variablen hinweg konstant ist. Eine Homoskedastizität wird als Vorbedingung für viele statistische Tests und Schätzverfahren angesehen und kann durch eine Gleichmäßigkeit der Streuung der Datenpunkte um die Regressionslinie in einem Scatterplot dargestellt werden.“ bezeichnet.
Um zu prüfen, ob diese Annahme erfüllt ist, wird der bekannte „Mauchly-Test“ verwendet, der häufig mit dem Programm SPSS durchgeführt wird. Wenn das Ergebnis des Tests einen p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. von .05 oder höher aufweist, kann man davon ausgehen, dass die Annahme der Sphärizität erfüllt ist. Ist das Ergebnis jedoch signifikant (p < .05), müssen die Freiheitsgrade reduziert werden, um Fehler zu vermeiden. In unserem Beispiel ist der Wert in der Spalte Sig. p<.001 und damit ist die Sphärizität nicht gegeben.

Es gibt in der statistischen Analyse eine Größe namens „Epsilon (ε)“, die angibt, wie stark die Sphärizität verletzt ist. Je nach Epsilon muss ein anderes Korrekturverfahren angewendet werden. Allerdings gibt es in der Statistik keine einheitlichen Richtlinien, wie genau vorgegangen werden soll. Ist der Epsilon-Wert 1, so sind alle Varianzen gleich, d. h. es liegt Homoskedastizität vor.
| Korrektur | Epsilon Wert |
|---|---|
| Huynh-Feld | ε > .75 |
| Greenhouse-Geisser | ε <= .75 |
In unserem Datensatz ist sollten wir die Greenhouse-Geisser-Korrektur verwenden.
Innersubjekteffekte
In den nächsten Tabellen ist unser Ziel den Haupteffekt zu bestimmen. Dies geschieht mit einem Blick auf die Tabelle Tests der Innersubjekteffekte.
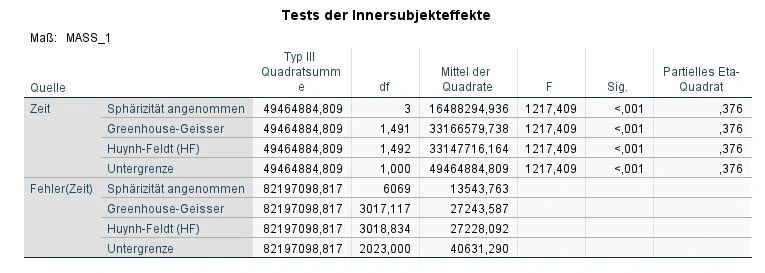
Wie wir diese Tabelle interpretieren hängt davon ab, was im Machly-Test vorher analysiert wurde. Wenn Die Sphärizität angenommen wurde, dann blicken wir auf die erste Spalte Zeit -> Sphärizität angenommen.
Falls die Sphärizität nicht gegen war und wir eine Korektur verwendet haben, sollten wir die entsprechende Zeile wählen. In unserem Beispiel wählen wir die Zeile Greenhouse-Geisser in der Zeile „Zeit“. Hier blicken wir auf die Spalte Signifikanz (Sig.). Wir haben ein signifikantes Ergebnis mit p<.001. Das bedeutet, dass die Gruppen unser ANOVA mit Messwiederholung sich signifikant unterscheiden.
Unsere finale Gleichung für die ANOVA mit Messwiederholung sieht wie folgt aus:
F(df bei Zeit*Gruppe, df bei Fehler(Zeit))=F-Wert, Sig., Partielles Eta-Quadrat
F(1.491,3017.12)=1217.41;p<.001, η² = .376
Post HocPost Hoc Post-hoc-Analysen sind Analysen, die nach der Durchführung einer Studie durchgeführt werden, um die Ergebnisse der Studie zu interpretieren und zu vertiefen. Analysen
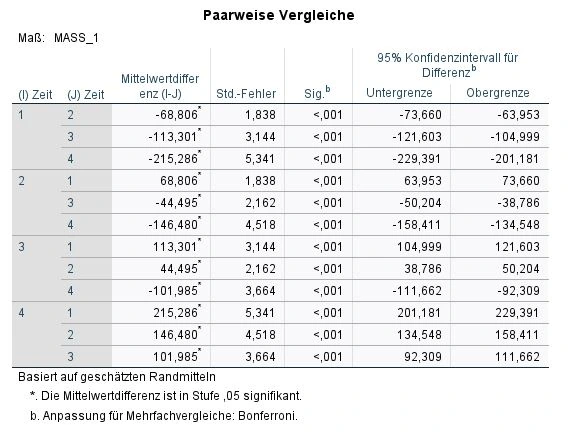
Wir wollen es genauer wissen und verwenden die Post-HocPost Hoc Post-hoc-Analysen sind Analysen, die nach der Durchführung einer Studie durchgeführt werden, um die Ergebnisse der Studie zu interpretieren und zu vertiefen.-Analysen um zu erfahren, welche Messzeitpunkte sich signifikant unterscheiden. Deshalb blicken wir auf die Tabelle Paarweise Vergleiche.
Häufig gestellte Fragen und Antworten: ANOVA mit Messwiederholung
Wann ANOVA mit Messwiederholung?
Die ANOVA mit Messwiederholung (auch als „gepaarte Samples ANOVA“ oder „Repeated Measures ANOVA“ bezeichnet) wird verwendet, wenn man den Einfluss von Variablen auf eine abhängige Variable untersucht, wobei dieselben Einheiten mehrfach gemessen werden. Beispiele für diese Art von Design könnten sein:
– Die Untersuchung des Einflusses von verschiedenen Behandlungen auf den Blutdruck von Patienten, wobei jeder Patient alle Behandlungen erhält
– Die Untersuchung des Einflusses von verschiedenen Trainingsmethoden auf die Muskelkraft von Sportlern, wobei jeder Sportler alle Trainingsmethoden erhält
– Die Untersuchung des Einflusses von verschiedenen Lehrmethoden auf die Leistungen von Schülern, wobei jeder Schüler alle Lehrmethoden erhält
Die ANOVA mit Messwiederholung ist geeignet, wenn es mehr als zwei Messzeitpunkte oder mehr als zwei Behandlungen gibt und wenn man sicherstellen möchte, dass die Unterschiede zwischen den Messzeitpunkten oder Behandlungen aufgrund der Variablen und nicht aufgrund von Unterschieden zwischen den Einheiten selbst entstehen. Sie ist auch geeignet, wenn man den Einfluss von Zeit auf die abhängige Variable untersuchen möchte.
Warum ANOVA und nicht T-Test?
Der T-Test ist ein wichtiges statistisches Verfahren, das verwendet wird, um zu überprüfen, ob es einen signifikanten Unterschied zwischen zwei Gruppen gibt. Der T-Test ist jedoch nur für Vergleiche zwischen zwei Gruppen geeignet.
Die ANOVA (Analysis of Variance) ist hingegen ein Verfahren, das verwendet wird, um zu überprüfen, ob es einen signifikanten Unterschied zwischen mehr als zwei Gruppen gibt. Die ANOVA wird verwendet, wenn man den Einfluss von einer oder mehreren Variablen (auch als Faktoren bezeichnet) auf eine abhängige Variable untersucht.Es gibt verschiedene Arten von ANOVA, je nachdem, wie die Gruppen miteinander verglichen werden. Die häufigsten sind die Einfaktor-ANOVA und die Mehrafaktor-ANOVA. Die Einfaktor-ANOVA wird verwendet, wenn es nur einen Faktor gibt, der die Gruppen unterscheidet, während die Mehrafaktor-ANOVA für den Vergleich von Gruppen geeignet ist, die sich in Bezug auf mehrere Faktoren unterscheiden.
Im Allgemeinen ist die ANOVA die geeignetere Wahl als der T-Test, wenn man den Unterschied zwischen mehr als 2 Gruppen analysieren möchte.
Was testet man mit ANOVA?
Die ANOVA (Analysis of Variance) ist ein statistisches Verfahren, das verwendet wird, um zu überprüfen, ob es einen signifikanten Unterschied zwischen den Mittelwerten von mehr als zwei Gruppen gibt. Mit der ANOVA wird also getestet, ob es einen Unterschied zwischen den Gruppen gibt oder ob der Unterschied zufällig entstanden ist.
Die ANOVA wird verwendet, um den Einfluss von einer oder mehreren Variablen (auch als Faktoren bezeichnet) auf eine abhängige Variable zu untersuchen. Die abhängige Variable ist das, was man messen möchte, während die Faktoren die Variablen sind, die den Unterschied zwischen den Gruppen verursachen sollen.
Zum Beispiel könnte man den Einfluss von Alter auf die Gedächtnisleistung untersuchen.In diesem Fall wären Alter der Faktor und Gedächtnisleistung die abhängige Variable. Man würde dann verschiedene Altersgruppen bilden und die Gedächtnisleistung in jeder Gruppe messen. Mit der ANOVA könnte man dann überprüfen, ob es einen signifikanten Unterschied zwischen den Altersgruppen in Bezug auf die Gedächtnisleistung gibt.
Wann ANOVA und wann MANOVA?
Die ANOVA (Analysis of Variance) und die MANOVA (Multivariate Analysis of Variance) sind beide statistische Verfahren, die verwendet werden, um den Einfluss von einer oder mehreren Variablen (auch als Faktoren bezeichnet) auf eine abhängige Variable zu untersuchen.
Der Hauptunterschied zwischen ANOVA und MANOVA besteht darin, dass die ANOVA nur für den Vergleich von Mittelwerten zwischen zwei oder mehr Gruppen geeignet ist, während die MANOVA für den Vergleich von Mittelwerten zwischen Gruppen auf der Basis von mehreren abhängigen Variablen geeignet ist.
Die ANOVA wird verwendet, wenn man den Einfluss von einer oder mehreren Variablen auf eine abhängige Variable untersucht, die numerisch ist und eine Normalverteilung aufweist. Die MANOVA wird verwendet, wenn man den Einfluss von einer oder mehreren Variablen auf zwei oder mehr abhängige Variablenabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. untersucht, die numerisch sind und möglicherweise keine Normalverteilung aufweisen.
Im Allgemeinen wählt man die ANOVA, wenn man den Unterschied zwischen den Gruppen in Bezug auf eine abhängige Variable untersuchen möchte, während die MANOVA geeignet ist, wenn man den Unterschied zwischen den Gruppen in Bezug auf mehrere abhängige Variablen untersuchen möchte.
Warum sind Messwiederholungen wichtig?
Messwiederholungen sind wichtig, weil sie es ermöglichen, den Einfluss von Variablen auf eine abhängige Variable zu untersuchen, während man sicherstellen kann, dass die Unterschiede zwischen den Messzeitpunkten oder Behandlungen aufgrund der Variablen und nicht aufgrund von Unterschieden zwischen den Einheiten selbst entstehen.
Wenn beispielsweise der Blutdruck von Patienten gemessen wird, könnte es sein, dass der Blutdruck eines Patienten an verschiedenen Tagen unterschiedlich ist, selbst wenn keine Veränderungen in Bezug auf Behandlungen oder andere Faktoren vorgenommen werden. Durch die Durchführung von Messwiederholungen kann man sicherstellen, dass jede Person an jedem Messzeitpunkt unter den gleichen Bedingungen gemessen wird, sodass die Ergebnisse vergleichbar sind.
Messwiederholungen sind auch wichtig, wenn man den Einfluss von Zeit auf eine abhängige Variable untersuchen möchte. Beispielsweise könnte man den Einfluss von verschiedenen Trainingsmethoden auf die Muskelkraft von Sportlern untersuchen, indem man die Muskelkraft vor und nach dem Training misst. Die Messwiederholungen ermöglichen es, den Einfluss des Trainings auf die Muskelkraft zu untersuchen, ohne dass die Unterschiede aufgrund von Unterschieden zwischen den Sportlern selbst entstehen.
Weiterführende Ressourcen zu ANOVA mit Messwiederholung in SPSS
Wann mehrfaktorielle Varianzanalyse durchführen?
Die mehrfaktorielle Varianzanalyse (auch als „Mehrafaktor-ANOVA“ oder „Factorial ANOVA“ bezeichnet) wird verwendet, wenn man den Einfluss von mehreren unabhängigen Variablen (auch als Faktoren bezeichnet) auf eine abhängige Variable untersuchen möchte. Die mehrfaktorielle Varianzanalyse ist geeignet, wenn man den Einfluss von mehreren Faktoren auf die abhängige Variable gleichzeitig untersuchen möchte, anstatt nur den Einfluss eines Faktors zu betrachten.
Die mehrfaktorielle Varianzanalyse ist hilfreich, wenn man den Einfluss von mehreren Variablen auf eine abhängige Variable untersuchen möchte, die numerisch ist und eine Normalverteilung aufweist. Sie ist auch geeignet, wenn man den Einfluss von Wechselwirkungen zwischen den Faktoren auf die abhängige Variable untersuchen möchte.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn