Warum gibt es extrem Werte in Daten?
Es gibt viele Gründe für AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind. und der einfachste Grund ist die natürliche Varianz in der menschlichen Population. Wir Menschen sind nicht alle gleich und unterscheiden uns auf vielfältiger Art und Weise. Eine Gewisse Streuung ist ganz normal. Was am Ende ein Ausreißer ist, hängt darüber hinaus stark von der untersuchten Stichprobe ab. Eine Person, die über zwei Meter groß ist würde für die Variable „Größe“ in einer Stichprobe schnell als Ausreißer deklariert werden. Untersuchen wir jedoch explizit Basketballmannschaften, könnte sich das wieder ändern.
Die Forschung interessiert sich in der Regel für den Durchschnitt der Gesellschaft, deren Ergebnisse sich auf so viele Personen wie möglich übertragen lassen. Daher ist es durchaus legitim, bei Variablen, die für die Analyse von Bedeutung sind, auszuschließen. Genauso richtig ist es, diese authentischen Fälle im Datensatz zu behalten. Eine pauschale Antwort kann leider nicht gegeben werden, weil es stets auf den jeweiligen Fall ankommt. Ein kleiner Tipp: Erhöhe die Anzahl der untersuchten Personen. So fallen Ausreißer weniger ins Gewicht und das Ausschließen hat einen geringeren Einfluss.
Menschen machen Fehler, dazu gehört auch falsche Dateneingabe durch Tippfehler, die zu absurden Folgen führen können. Das gilt auch für Messfehler, die beispielsweise durch eine fehlerhafte Kalibrierung Fehler und damit falsche Daten produzieren. Hier sollte man aufpassen, dass nicht zu viele Daten aufgrund Messfehler erzeugt wurden, da diese als systematische Fehler so häufig im Datensatz vorkommen, dass diese ein Teil der Daten und nicht mehr als Ausreißer identifiziert werden. Aus diesen Gründen sollten Ausreißer aus Dateneingabefehler ausgeschlossen werden.
Die Analyse der Ausreißer mit Box-Plot Diagrammen
Es gibt mehrere Möglichkeiten, um Ausreißer in Datensätzen zu identifizieren. In der Wissenschaft sind wir uns nicht ganz einig, welche Methode die beste bzw. die schlüssigste ist. Das liegt daran, dass es normal ist, dass Datensätze nicht untereren Erwartungshaltungen entsprechen. Die Beurteilung, ab wann ein Datensatz nicht mehr normal ist, ist immer subjektiv.
Die einfachste Möglichkeit in SPSS Ausreißer zu finden sind Box-Plot Diagramme. Mithilfe der Box-Plot Diagramme zeigt uns SPSS direkt, welche Fälle in den Datensätzen Ausreißer sein könnten. Diese Analyse können wir für jede Variable durchführen.
Erklärung: Was ist ein Box-Plot-Diagramm?
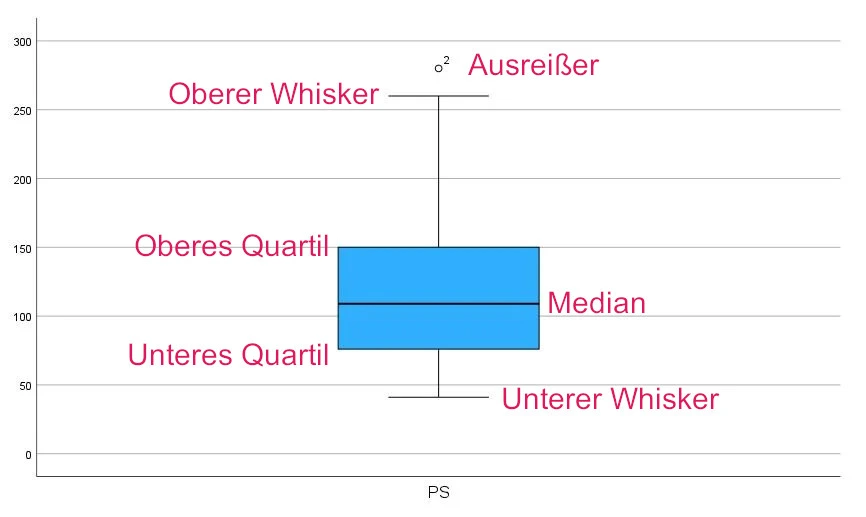
Ein Box-Plot-Diagramm, auch als Box-and-Whisker-Diagramm bekannt, ist ein grafisches Darstellungsmittel, das verwendet wird, um die Verteilung von Daten darzustellen. Es zeigt den Median, die Interquartile Range (IQR) und die Ausreißer (auch als Extreme bezeichnet) einer Datenmenge.
Der blaue Bauch (Box) des Box-Plots grenzt das untere und obere Quartil im Datensatz ein. Das bedeutet, dass 50% unserer Daten sich in diesem Bereich befinden. In der Mitte teilt der Median als Strich die Box in zwei Hälften. Er symbolisiert, wo sich jeweils 50 % der Daten liegen. Die dünnen Antennen werden als oberer bzw. unterer Whisker bezeichnet und sind von der Länge maximal das 1,5-Fache des Interquartilabsstands (Länge der Box) lang und können unterschiedlich groß sein, weil sie sich an den konkreten Datenpunkten, die sich innerhalb dieser Grenze befinden, richten. Werte außerhalb der Whiskers werden als Ausreißer behandelt.
Anleitung Ausreißer in SPSS finden
Statistische Ausreißer in SPSS mit Box-Plot finden
Auswahl im Menü

Wir klicken auf Analysieren > Deskriptive Statistiken > Explorative Datenanalyse.
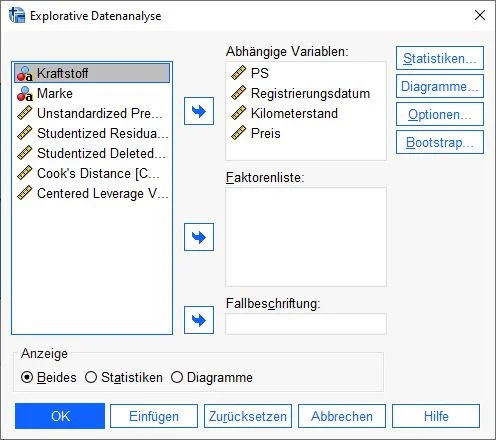
Dialogbox Explorative Datenanalyse: Einstellungen für Ausreißer in SPSS finden

Es öffnet sich das Explorative Datenanalyse Dialogfenster.
In der linken Spalte befinden sich alle verfügbaren Variablen. Wir klicken auf eine Variable mit der linken Maustaste und halten diese gedrückt, während wir den Mauszeiger über das Feld Abhängige Variablenabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. bewegen. Dort angekommen, lassen wir die Maustaste los. Durch diese Aufheben-und-Loslassen-Technik (Drag-and-drop) können wir in SPSS schnell Variablen hin- und herschieben. Mit dieser Technik ziehen wir alle Variablen, die analysiert werden, in das Feld Abhänge Variablen.
Jede Variable, die wir in das Feld „Abhängige Variablen“ ziehen, erzeugt nach Berechnung ein Diagramm. Diese Diagramme zeigen uns mögliche Ausreißer an.
Hinweis: Alternativ kann der blaue Knopf mit dem Pfeil verwendet werden, um Variablen in die entsprechenden Felder zu verschieben.
Weiterer Hinweis: Falls es mehrere Gruppen gibt, die wir vergleichen, ziehen wir die unabhängige Variable (UV) in das Feld Faktorenliste.
In der Gruppe Anzeige setzen wir den Marker auf die Option Beides.
Nächster Schritt: Wir klicken auf die Schaltfläche Diagramme.
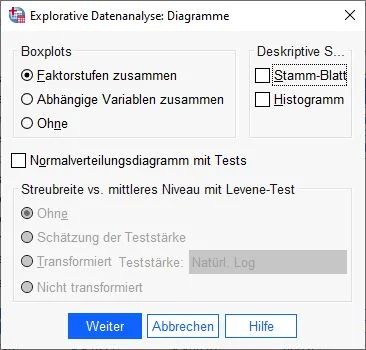
Dialogfenster: Diagramme

Im Dialogfenster Diagramme interessieren wir uns für das Feld Box-Plots und stellen sicher, dass die Option Faktorstufen zusammen gewählt ist. Wir klicken auf Weiter, um die Eingaben zu bestätigen.
Wir sind bereit

Jetzt sind wir bereit und klicken unten auf OK, um die explorative Datenanalyse zu starten und unsere Diagramme zu sehen.
Analyse der Diagramme: Ausreißer identifizieren in SPSS Beispiel 1

SPSS gibt uns eine Übersicht mit den Ausreißern anhand von Box-Plot Diagrammen.
Jeder Datenpunkt, der unverhältnismäßig groß oder klein ist, wird in dieser Ansicht aufgeführt. Falls ein Wert mehr als 1,5 Standardabweichungen vom Mittelwert der Variable entfernt ist, gilt dieser als leichter Ausreißer und wird mit einem kleinen Kreis(°) dargestellt. Sogenannte extreme Ausreißer sind mehr als 3 Standardabweichungen vom Mittelwert entfernt und werden durch einen Stern (*) visualisiert. Die Nummer neben dem Symbol zeigt, um welchen Fall es sich handelt.
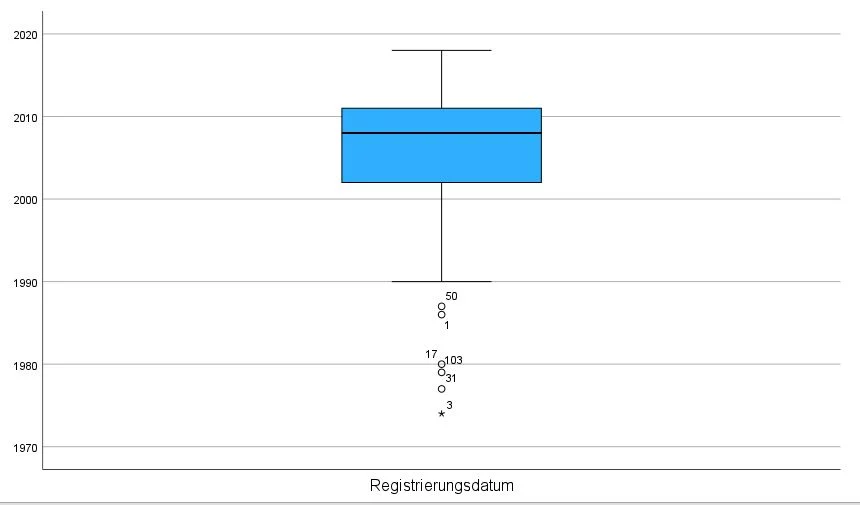
In unserem Beispiel sehen wir, dass für die Variable „PS“ mehrere leichte Ausreißer identifiziert wurden. Datenpunkt 50, 1, 17, 103 und 31 gehören dazu. Es gibt einen extremen Ausreißer: Fall Nummer 3.
Analyse der Diagramme: Ausreißer identifizieren in SPSS Beispiel 2

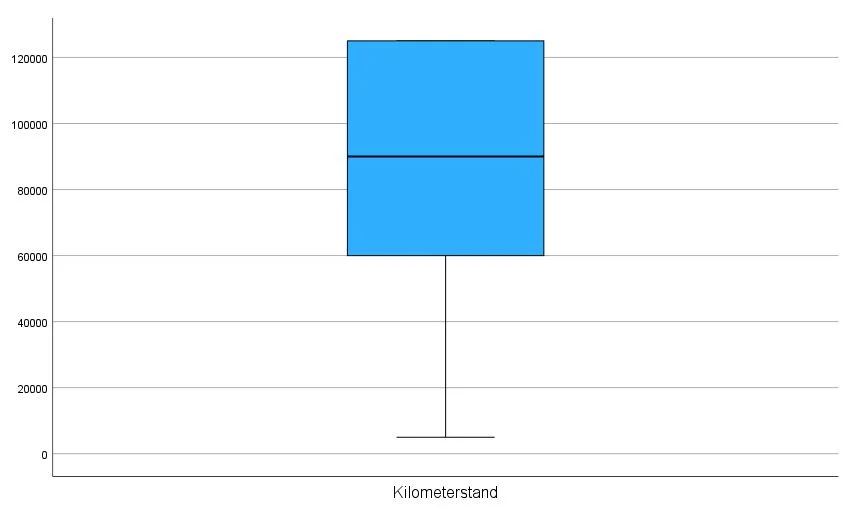
Im Gegensatz zu der Variable „PS“ findet unsere Methode bei der Variable „Kilometerstand“ keine Ausreißer. Das Box-Plot Diagramm zeigt uns, dass die Daten nicht gleich verteilt sind, was erstmal nicht schlimm ist.
Analyse der Diagramme: Ausreißer identifizieren in SPSS Beispiel 3

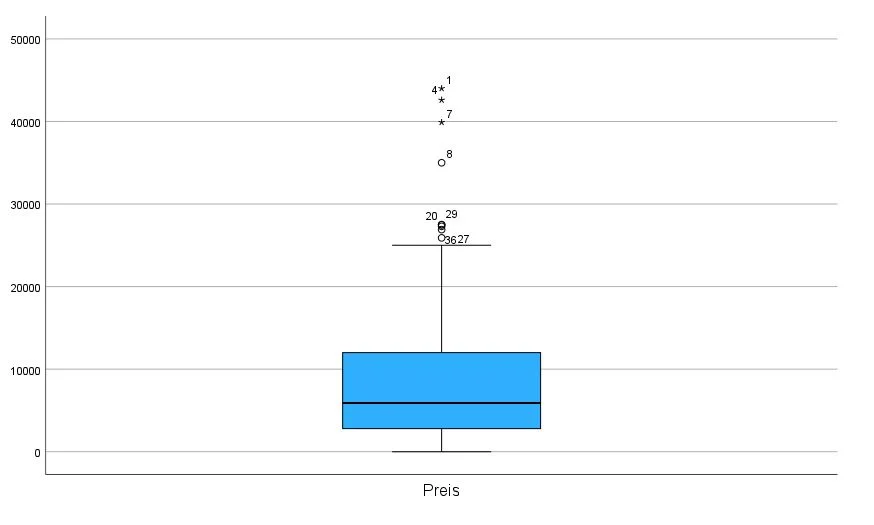
Das letzte Beispiel ist die Variable „Preis“. Hier finden wir mit dieser Methode mehrere Ausreißer nach oben hin. Es gibt demnach besonders teure Automobile im Gebrauchtmarkt, die nicht unseren Erwartungen anhand der Daten entsprechen. Das ist nicht ganz unrealistisch.
ResiduenResiduen Residuen sind die Abweichungen zwischen den beobachteten Daten und den durch ein statistisches Modell vorhergesagten Daten und werden verwendet, um die Anpassung des Modells an die Daten zu beurteilen und um mögliche Muster oder Trends in den Daten zu erkennen. Sie können auch verwendet werden, um die Validität und Zuverlässigkeit von Vorhersagemodellen zu überprüfen.
Identifikation von Ausreißern mit Residuen, Hebelwerten und Cook-Distanzen
Wenn dir die Box-Plot-Diagramme nicht ausreichen, können wir tiefer in die Materie eintauchen und mit mehreren Methoden Ausreißer im Datensatz identifizieren. Diese Anleitung verwendet Fallweise Diagnose, studentisierte ausgeschlossene Residuen, Hebelwerte und Cook-Distanzen.
Analyse mit Fallweise Diagnose
Was machen wir mit den Ausreißern?
Falls wir Datenpunkte entdeckt haben, die zu weit gestreut von Mittel des Datensatzes sind, gibt es mehrere Möglichkeiten, mit der Analyse fortzufahren:
In der Regel gilt: Extreme Ausreißer sollten aus dem Datensatz entfernt werden, leichte Ausreißer können, müssen aber nicht entfernt werden. Wie mit Ausreißern umgegangen wird, ist selbst bei den Forschern umstritten. Die Berechnung von Ausreißern basiert zwar auf mathematischen Formeln, die eine objektive Bewertung ermöglichen und sind gleichzeitig dennoch, gerade bei kleineren Datenmengen umstritten. Darüber hinaus, können durch zu schnelle Entfernung der Ausreißer die Daten geschönt werden, in dem alle nicht passenden Ergebnisse entfernt werden. Übrigens: Die ersten Ozonlöcher wurden damals auch als statistische Ausreißer ignoriert.
Ergebnisse darstellen
Wenn keine Ausreißer gefunden wurden: Im Datensatz befanden sich keine Ausreißer.
There were no outliers in the data.
Wenn Ausreißer gefunden wurden: Drei Fälle wiesen extreme Werte auf und wurden von der weiteren Datenauswertung ausgeschlossen.
Three cases were excluded from further analysis due to extreme values
Häufig gestellte Fragen und Antworten: Ausreißer finden in SPSS
Wie bestimmt man Ausreißer?
Ausreißer, auch als „Outliers“ bezeichnet, sind extreme Werte in einer Datenmenge, die deutlich von den übrigen Werten abweichen. Sie können dazu führen, dass die Statistiken, die auf den Daten berechnet werden, verfälscht werden und somit die Analyse beeinträchtigen.
Es gibt verschiedene Möglichkeiten, Ausreißer in einer Datenmenge zu bestimmen, je nach dem spezifischen Kontext und den verfügbaren Daten. Hier sind einige Beispiele:
– Box-Plot: Ein Boxplot ist ein grafisches Darstellungsverfahren, das verwendet wird, um die Verteilung von Daten zu visualisieren. Ausreißer können in einem Boxplot als Werte identifiziert werden, die außerhalb der „Whiskers“ liegen, die die obere und untere Grenze des Boxplots darstellen.
– StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. : Die Standardabweichung ist ein Maß für die Streuung der Daten um den Mittelwert. Ausreißer können als Werte identifiziert werden, die mehr als zwei Standardabweichungen von dem Mittelwert entfernt sind.
– Z-Score: Der Z-Score ist ein Maß dafür, wie weit ein bestimmter Wert von dem Mittelwert der Datenmenge entfernt ist. Man kann auch Ausreißer als Werte identifizieren, die einen Z-Score von mehr als 3 oder weniger als -3 haben. Der Z-Score gibt an, wie viele Standardabweichungen ein Wert von dem Mittelwert entfernt ist.
Es gibt noch weitere Methoden wie den Grupps Test, auf den wir nicht weiter eingehen.
Welche Ausreißer ausschließen?
Ausreißer, auch als „extrem hohe oder niedrige Werte“ bezeichnet, sind Datenpunkte, die signifikant von den anderen Datenpunkten in einer Stichprobe abweichen. Sie können das Ergebnis von Messfehlern, menschlichen Fehlern oder anderen ungewöhnlichen Ereignissen sein und können die Analyse von Daten beeinflussen.
Es gibt verschiedene Möglichkeiten, wie Ausreißer in der Statistik behandelt werden können:
– Ignorieren: In manchen Fällen können Ausreißer einfach ignoriert werden, wenn sie wenig Einfluss auf die Analyse haben.
– Entfernen: In manchen Fällen können Ausreißer entfernt werden, um die Analyse nicht zu beeinflussen. Dies kann jedoch dazu führen, dass wichtige Informationen verloren gehen.
– Korrigieren: In manchen Fällen können Ausreißer korrigiert werden, indem die Ursache für den Ausreißer identifiziert und behoben wird.
– Verwenden robusterer Statistiken: In manchen Fällen können robustere Statistiken verwend
Wann gilt ein Wert als Ausreißer?
Ein Wert wird als Ausreißer betrachtet, wenn er signifikant von den anderen Werten in einer Stichprobe abweicht. Ob ein Wert als Ausreißer betrachtet wird, hängt jedoch von verschiedenen Faktoren ab, wie z.B. der Art der Daten, der Größe der Stichprobe und den verwendeten Analysemethoden.
Es ist wichtig zu beachten, dass die Definition von Ausreißern subjektiv ist und dass es keine definitive Grenze gibt, die festlegt, ab wann ein Wert als Ausreißer betrachtet wird. Du solltest daher immer sorgfältig überlegen, ob ein Wert als Ausreißer betrachtet werden sollte und wie Ausreißer in deiner Analyse behandelt werden sollten.
Was ist eine Ausreißeranalyse?
Eine Ausreißeranalyse in der Statistik ist eine Methode zur Untersuchung von extrem hohen oder niedrigen Werten in einer Stichprobe, auch als Ausreißer bezeichnet. Die Analyse von Ausreißern kann helfen, mögliche Fehler oder ungewöhnliche Ereignisse in den Daten zu identifizieren und zu verstehen, wie sie die Analyse beeinflussen können.
Es gibt verschiedene Möglichkeiten, wie man eine Ausreißeranalyse durchführen kann. Eine Möglichkeit ist die Verwendung von Boxplots, um Ausreißer visuell zu identifizieren. Eine andere Möglichkeit ist die Verwendung von statistischen Tests, um festzustellen, ob ein Wert als Ausreißer betrachtet werden kann.
Wenn du eine Ausreißeranalyse durchführen möchtest, solltest du zunächst entscheiden, ob du Ausreißer entfernen, ignorieren oder korrigieren möchtest. Du solltest auch entscheiden, ob du robustere Statistiken verwenden möchtest, die weniger anfällig für Ausreißer sind. Nachdem du diese Entscheidungen getroffen hast, kannst du die Ausreißer entsprechend behandeln und deine Analyse fortsetzen. Es ist wichtig, dass du die Auswirkungen von Ausreißern auf deine Analyse verstehst und entsprechend berücksichtigst.
Warum sind Ausreißer ein Problem?
Ausreißer, auch als „extrem hohe oder niedrige Werte“ bezeichnet, sind Datenpunkte, die signifikant von den anderen Datenpunkten in einer Stichprobe abweichen. Sie können das Ergebnis von Messfehlern, menschlichen Fehlern oder anderen ungewöhnlichen Ereignissen sein und können die Analyse von Daten beeinflussen.
Wenn Ausreißer nicht berücksichtigt werden, können sie dazu führen, dass die Analyse von Daten unzuverlässig wird und zu falschen Schlussfolgerungen führt. Aus diesem Grund ist es wichtig, dass du die Auswirkungen von Ausreißern auf deine Analyse verstehst und entsprechend berücksichtigst.
Welche Kennzahlen sind robust gegen Ausreißer?
Einige Kennzahlen sind weniger anfällig für Auswirkungen von Ausreißern als andere. Diese Kennzahlen werden als robuste Statistiken bezeichnet. Hier sind einige Beispiele für robuste Statistiken:
– Median: Der Median ist der mittlere Wert in einer Stichprobe und wird berechnet, indem man die Werte sortiert und den Wert in der Mitte findet. Der Median ist weniger anfällig für Auswirkungen von Ausreißern als der Mittelwert.
– Interquartilsbereich (IQR): Der Interquartilsbereich ist der Bereich zwischen dem unteren Quartil (25. Percentil) und dem oberen Quartil (75. Percentil) in einer Stichprobe. Der IQR ist weniger anfällig für Auswirkungen von Ausreißern als der Standardabweichungsbereich.
– Median Absolute Deviation (MAD): Die Median Absolute Deviation ist der Median der Abweichungen zwischen den Werten in einer Stichprobe und dem Median der Stichprobe. Die MAD ist weniger anfällig für Auswirkungen von Ausreißern als die Standardabweichung.
Es ist wichtig zu beachten, dass keine Statistik vollständig robust gegen Ausreißer ist und dass es in der Regel auf mehrere Statistiken und Methoden ankommt, um eine zuverlässige Einschätzung von Daten zu erhalten. Es ist auch wichtig, dass du die Annahmen und Einschränkungen jeder Statistik verstehst und berücksichtigst, bevor du sie verwendest.
Wann sollte man Ausreißer entfernen?
Es gibt keine definitive Antwort darauf, wann man Ausreißer entfernen sollte, da dies von der Art der Studie und der verwendeten Analysemethoden abhängt. In der Regel sollten Ausreißer jedoch entfernt werden, wenn sie das Ergebnis der Analyse erheblich beeinflussen.
Ein Ausreißer kann das Ergebnis einer Analyse beeinflussen, indem er:
– die Schätzung von Mittelwert und Standardabweichung verfälscht
– die Interpretation von KorrelationenKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird. oder Regressionsanalysen beeinflusst
– den Signifikanztest beeinflusst, wodurch die Nullhypothese zu Unrecht verworfen werden könnte
Wenn du entscheidest, Ausreißer zu entfernen, solltest du sorgfältig überlegen, ob diese Entscheidung für deine Studie angemessen ist. Du solltest auch sicherstellen, dass du die Auswirkungen von Ausreißern auf deine Analyse verstehst und entsprechend berücksichtigst.
Es ist auch wichtig zu beachten, dass Ausreißer nicht immer entfernt werden sollten. In manchen Fällen können Ausreißer wichtige Informationen enthalten und ihre Entfernung könnte zu wichtigen Datenverlust führen. In solchen Fällen könnte es besser sein, Ausreißer zu ignorieren oder zu korrigieren.
Ist der Median robust gegen Ausreißer?
Der Median ist in der Regel weniger anfällig für Auswirkungen von Ausreißern als der Mittelwert. Der Median ist der mittlere Wert in einer Stichprobe und wird berechnet, indem man die Werte sortiert und den Wert in der Mitte findet. Der Median wird nicht durch extreme Werte beeinflusst, da er lediglich den Wert in der Mitte der Stichprobe misst.
Das bedeutet jedoch nicht, dass der Median vollständig robust gegen Ausreißer ist. Der Median kann immer noch von Ausreißern beeinflusst werden, insbesondere wenn es sehr viele Ausreißer gibt oder wenn sich die Ausreißer in einer bestimmten Häufigkeit oder in einem bestimmten Bereich der Stichprobe befinden.
Es ist wichtig zu beachten, dass keine Statistik vollständig robust gegen Ausreißer ist und dass es in der Regel auf mehrere Statistiken und Methoden ankommt, um eine zuverlässige Einschätzung von Daten zu erhalten. Du solltest daher immer die Annahmen und Einschränkungen jeder Statistik verstehen und berücksichtigen, bevor du sie verwendest.
Literatur:
Field, Andy (2018), Discovering Statistics Using IBM SPSS Statistics, S. 227-229 sowie 240-243.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn