GrundgesamtheitGrundgesamtheit Die Grundgesamtheit ist die komplette Menge an Elementen oder Individuen, die für eine bestimmte Studie oder Umfrage relevant sind. Sie kann sich auf die Bevölkerung, eine bestimmte Region oder eine bestimmte Gruppe von Menschen beziehen. und Stichproben erklärt
Eine Grundgesamtheit ist eine Menge von Objekten, die von Interesse sind und über die man bestimmte Aussagen treffen möchte. Eine Stichprobe ist eine Teilmenge der Grundgesamtheit, die ausgewählt wird, um Aussagen über die Grundgesamtheit zu treffen. Die Stichprobe wird dazu verwendet, um Schätzungen über die Merkmale der Grundgesamtheit zu treffen.
Die Größe der Stichprobe hängt von der Größe der Grundgesamtheit und von der Genauigkeit ab, die man erreichen möchte. In der Regel wird die Stichprobe so gewählt, dass sie repräsentativ für die Grundgesamtheit ist, damit die Ergebnisse auf die Grundgesamtheit übertragbar sind.
Was ist eine repräsentative Stichprobe?
Eine repräsentative Stichprobe ist eine Stichprobe, die die Merkmale der Grundgesamtheit widerspiegelt. Dies bedeutet, dass die Stichprobe ähnlich wie die Grundgesamtheit in Bezug auf die wichtigsten Merkmale zusammengesetzt ist.
Eine repräsentative Stichprobe kann auf verschiedene Weise ausgewählt werden, zum Beispiel durch Zufallsauswahl oder durch systematisches Sampling. Es ist wichtig, dass die Stichprobe wirklich zufällig aus der Grundgesamtheit ausgewählt wird, um sicherzustellen, dass sie tatsächlich repräsentativ ist.
Eine nicht repräsentative Stichprobe hingegen kann zu Verzerrungen führen und die Ergebnisse verfälschen, da sie nicht die Merkmale der Grundgesamtheit widerspiegelt.
Stichprobenbeziehung
In der Statistik geht es darum, Aussagen über eine bestimmte Menge von Objekten, der sogenannten Grundgesamtheit, zu treffen. Die Grundgesamtheit kann sehr groß sein und es ist oft nicht möglich oder praktikabel, alle Elemente der Grundgesamtheit zu untersuchen. Stattdessen wählt man eine Teilmenge der Grundgesamtheit aus, die Stichprobe genannt wird, und untersucht diese.
Die Stichprobe wird dazu verwendet, Schätzungen über die Merkmale der Grundgesamtheit zu treffen. Es ist wichtig, dass die Stichprobe repräsentativ für die Grundgesamtheit ist, d.h. dass sie die Merkmale der Grundgesamtheit widerspiegelt. Auf diese Weise können die Ergebnisse auf die Grundgesamtheit übertragen werden.
Die Stichprobenbeziehung beschreibt die Beziehung zwischen der Stichprobe und der Grundgesamtheit. Um die Stichprobenbeziehung zu verstehen, muss man sich bewusst machen, dass die Stichprobe nur eine Teilmenge der Grundgesamtheit ist und dass die Ergebnisse, die man aus der Stichprobe gewinnt, nur für die Stichprobe gelten. Die Ergebnisse können jedoch auf die Grundgesamtheit übertragen werden, wenn die Stichprobe repräsentativ ist.
Formen der Stichprobenerhebung
Es gibt verschiedene Methoden der Stichprobenerhebung, die sich in der Art der Auswahl der Stichprobe unterscheiden:
- Zufallsauswahl: Hierbei werden alle Elemente der Grundgesamtheit gleichberechtigt in die Stichprobe aufgenommen. Diese Methode ist die transparenteste und faireste Methode, da jedes Element gleiche Chancen hat, in der Stichprobe enthalten zu sein. Allerdings ist die Zufallsauswahl nicht immer die beste Methode, da sie manchmal zu sehr ungleichmäßigen Stichproben führen kann.
- Stratifizierte Auswahl: Hierbei wird die Grundgesamtheit in Untergruppen (Straten) unterteilt und aus jeder Untergruppe eine Stichprobe gezogen. Diese Methode wird verwendet, wenn bestimmte Merkmale oder Eigenschaften in der Stichprobe gut vertreten sein sollen. Zum Beispiel könnten bei einer Umfrage zur politischen Einstellung die Altersschichten als Strata verwendet werden, um sicherzustellen, dass alle Altersschichten gut vertreten sind.
- Klusterauswahl: Hierbei werden große Gruppen von Elementen (Klumpen oder Cluster) ausgewählt und die Stichprobe wird innerhalb dieser Kluster gezogen. Diese Methode wird verwendet, wenn die Elemente der Grundgesamtheit in natürlichen Gruppen vorliegen, zum Beispiel Schulen oder Gemeinden. Die Klusterauswahl ist in der Regel kostengünstiger als die anderen Methoden, aber sie kann zu ungleichmäßigen Stichproben führen und ist weniger genau als die Zufallsauswahl.
Es gibt auch andere Methoden der Stichprobenerhebung wie die Quota-Methode oder die Zwangsmethode, die jedoch weniger verbreitet sind und weniger zuverlässig sind als die oben genannten Methoden. Es ist wichtig, dass die geeignete Stichprobenmethode sorgfältig ausgewählt wird und dass die Stichprobe ausreichend groß ist, um valide Rückschlüsse auf die Grundgesamtheit ziehen zu können.
Unterschiede in der Schreibweise zwischen Stichprobe und Grundgesamtheit
| Schreibweisen | Stichprobe | Grundgesamtheit |
|---|---|---|
| Verwendete Buchstaben | Lateinische Buchstaben | Griechische Buchstaben |
| Anzahl | N, n | N |
| Mittelwert | M | μ |
| StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. | SD, s | σ |
Die Größe der Stichprobe bestimmen
Der Stichprobenumfang ist die Größe der Stichprobe, d.h. die Anzahl der Elemente in der Stichprobe. Es gibt verschiedene Faktoren, die bei der Bestimmung des Stichprobenumfangs berücksichtigt werden müssen.
Einer der wichtigsten Faktoren ist die Größe der Grundgesamtheit. Je größer die Grundgesamtheit ist, desto größer sollte in der Regel auch die Stichprobe sein, um eine ausreichende Genauigkeit zu erreichen.
Weiterhin spielt die gewünschte Genauigkeit der Schätzungen eine Rolle bei der Bestimmung des Stichprobenumfangs. Je größer die gewünschte Genauigkeit ist, desto größer muss in der Regel auch die Stichprobe sein.
Es gibt verschiedene Formeln und Tabellen, die zur Bestimmung des Stichprobenumfangs verwendet werden können, die auf verschiedenen Faktoren wie der Größe der Grundgesamtheit, der gewünschten Genauigkeit und der Varianz der Merkmale der Grundgesamtheit basieren. Ein Statistiker oder ein Experte in dem betreffenden Bereich kann bei der Bestimmung des Stichprobenumfangs behilflich sein.
Stichprobengröße berechnen
Die Stichprobengröße kann mit Hilfe des z-Werts, der Verteilung der Grundgesamtheit und der Fehlergrenze berechnet werden.
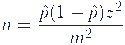
- n = Stichprobengröße
- z = der z-Wert gibt an, wie viele Standardabweichungen ein Schätzwert von der wahren Grundgesamtheit entfernt sein darf, damit die Ergebnisse als akzeptabel angesehen werden. Je größer der z-Wert ist, desto größer muss die Stichprobe sein, um eine ausreichende Genauigkeit zu erreichen.
- p̂ = Die Verteilung der Grundgesamtheit spielt ebenfalls eine Rolle bei der Bestimmung der Stichprobengröße. Wenn die Grundgesamtheit eine normalverteilte oder symmetrische Verteilung hat, kann man den z-Wert verwenden, um die Stichprobengröße zu berechnen. Wenn die Verteilung jedoch nicht normalverteilt oder symmetrisch ist, müssen andere Methoden zur Bestimmung der Stichprobengröße verwendet werden.
- m =Die Fehlergrenze gibt an, wie genau die Schätzungen sein sollen. Je größer die Fehlergrenze ist, desto größer kann die Stichprobe sein, da weniger Genauigkeit erforderlich ist. Je kleiner die Fehlergrenze ist, desto größer muss die Stichprobe sein, um die gewünschte Genauigkeit zu erreichen.
Um die Stichprobengröße zu berechnen, werden diese Faktoren in einer Formel verwendet, die auf dem KonfidenzintervallKonfidenzintervalle Konfidenzintervalle sind Schätzungen der wahren Population, die angeben, mit welcher Wahrscheinlichkeit sich die wahre Population innerhalb eines bestimmten Bereichs befindet. Sie werden verwendet, um die Unsicherheit von Schätzungen auszudrücken und die Stabilität von Statistiken zu beurteilen und werden häufig in der Statistik und der Datenanalyse verwendet. für den Schätzwert basiert.
Standardfehler bei Stichproben
Der Standardfehler ist ein Maß dafür, wie sehr sich die Stichprobe von der Grundgesamtheit unterscheidet. Er gibt an, wie genau die Schätzungen aufgrund der Stichprobe sind und wie sehr sie von den tatsächlichen Werten in der Grundgesamtheit abweichen können.
Der Standardfehler wird aus der Standardabweichung der Stichprobe berechnet und gibt an, wie stark sich die Werte in der Stichprobe voneinander unterscheiden. Je größer der Standardfehler ist, desto größer ist die Unsicherheit bei den Schätzungen und desto weniger genau sind diese.
Der Standardfehler ist wichtig, weil er dazu verwendet werden kann, KonfidenzintervalleKonfidenzintervalle Konfidenzintervalle sind Schätzungen der wahren Population, die angeben, mit welcher Wahrscheinlichkeit sich die wahre Population innerhalb eines bestimmten Bereichs befindet. Sie werden verwendet, um die Unsicherheit von Schätzungen auszudrücken und die Stabilität von Statistiken zu beurteilen und werden häufig in der Statistik und der Datenanalyse verwendet. für Schätzwerte zu berechnen. Konfidenzintervalle geben an, mit welcher Wahrscheinlichkeit sich der wahre Wert in der Grundgesamtheit innerhalb eines bestimmten Bereichs um den Schätzwert befindet. Je kleiner der Standardfehler ist, desto enger ist das Konfidenzintervall und desto genauer sind die Schätzwerte.
Es ist wichtig zu beachten, dass der Standardfehler nur ein Maß für die Unsicherheit der Schätzwerte aufgrund der Stichprobe ist und nicht die Unsicherheit aufgrund anderer Faktoren, die die Grundgesamtheit betreffen, berücksichtigt. Deshalb ist es wichtig, dass die Stichprobe repräsentativ für die Grundgesamtheit ist, um sicherzustellen, dass der Standardfehler ein aussagekräftiges Maß für die Unsicherheit der Schätzwerte ist.
Vollerhebung oder Stichproben?
Eine Vollerhebung ist eine Art von Umfrage, bei der alle Elemente einer definierten Bevölkerung befragt werden. Das bedeutet, dass keine Elemente der Bevölkerung ausgeschlossen werden und alle Elemente die gleichen Chancen haben, in der Umfrage enthalten zu sein. Eine Vollerhebung bietet eine genauere und zuverlässigere Darstellung der Meinungen, Einstellungen oder Merkmale der Bevölkerung, da alle Elemente der Bevölkerung in der Umfrage berücksichtigt werden. Allerdings ist eine Vollerhebung in der Regel teurer und zeitaufwendiger als eine Stichprobe.
Eine Stichprobe ist eine Art von Umfrage, bei der nur eine Teilmenge der Bevölkerung befragt wird. Das bedeutet, dass einige Elemente der Bevölkerung ausgeschlossen werden und nicht alle Elemente die gleichen Chancen haben, in der Umfrage enthalten zu sein. Eine Stichprobe ist in der Regel billiger und schneller als eine Vollerhebung, da nur eine Teilmenge der Bevölkerung befragt wird. Allerdings kann die Stichprobe weniger genau und zuverlässig sein, da nicht alle Elemente der Bevölkerung berücksichtigt werden und es besteht die Möglichkeit, dass die Stichprobe nicht repräsentativ für die gesamte Bevölkerung ist.
Die Vorteile einer Stichprobe gegenüber einer Vollerhebung
- Kosten: Stichproben sind in der Regel billiger als Vollerhebungen, da nur eine Teilmenge der Bevölkerung befragt wird.
- Zeit: Stichproben sind schneller als Vollerhebungen, da nur eine Teilmenge der Bevölkerung befragt wird.
- Flexibilität: Stichproben bieten mehr Flexibilität bei der Auswahl der Elemente, die in der Umfrage enthalten sein sollen.
- Präzision: Mit der richtigen Stichprobenmethode und ausreichend großer Stichprobe kann die Präzision einer Stichprobe der einer Vollerhebung entsprechen.
- Repräsentativität: Mit der richtigen Stichprobenmethode und ausreichend großer Stichprobe kann eine Stichprobe ebenso repräsentativ für die Bevölkerung sein wie eine Vollerhebung.
Häufig gestellte Fragen und Antworten: Stichproben
Was ist die Grundgesamtheit?
Die Grundgesamtheit ist die komplette Bevölkerung, die für eine bestimmte Studie von Interesse ist. Sie umfasst alle Elemente der Bevölkerung, die bestimmte Merkmale oder Eigenschaften aufweisen, die für die Studie relevant sind. Die Grundgesamtheit ist das Hauptuntersuchungsobjekt und bildet die Basis für die Auswahl von Stichproben oder für eine Vollerhebung. Sie wird auch als Universum bezeichnet.
Die Größe der Grundgesamtheit kann sehr unterschiedlich sein und hängt von der Art der Studie und dem Untersuchungsgebiet ab. Sie kann zum Beispiel alle Menschen in einem Land oder alle Kunden eines Unternehmens umfassen. Es ist wichtig, dass die Grundgesamtheit klar definiert und beschrieben wird, damit die Ergebnisse der Studie auf die Grundgesamtheit generalisiert werden können.
Was ist eine Stichprobe?
Eine Stichprobe ist eine Art von Umfrage, bei der nur eine Teilmenge der Bevölkerung befragt wird. Das bedeutet, dass einige Elemente der Bevölkerung ausgeschlossen werden und nicht alle Elemente die gleichen Chancen haben, in der Umfrage enthalten zu sein. Eine Stichprobe wird verwendet, um Rückschlüsse auf die Meinungen, Einstellungen oder Merkmale der gesamten Bevölkerung zu ziehen.
Die Größe der Stichprobe hängt von der Größe der Grundgesamtheit und der gewünschten Genauigkeit ab. Je größer die Stichprobe, desto genauer und zuverlässiger sind die Ergebnisse in der Regel. Allerdings ist auch die Größe der Stichprobe begrenzt durch den verfügbaren Zeit- und Kostenrahmen. Es ist wichtig, dass die Stichprobe repräsentativ für die Grundgesamtheit ist, um valide Rückschlüsse ziehen zu können.
Wie von der Stichprobe auf die Grundgesamtheit schließen?
Um von der Stichprobe auf die Grundgesamtheit schließen zu können, muss die Stichprobe repräsentativ für die Grundgesamtheit sein. Repräsentativität bedeutet, dass die Stichprobe die wichtigsten Merkmale und Eigenschaften der Grundgesamtheit widerspiegelt. Wenn die Stichprobe repräsentativ ist, können die Ergebnisse der Stichprobe auf die Grundgesamtheit generalisiert werden.
Es gibt verschiedene Methoden, um eine repräsentative Stichprobe zu erhalten, zum Beispiel:
– Zufallsauswahl: Hierbei werden alle Elemente der Grundgesamtheit gleichberechtigt in die Stichprobe aufgenommen.
– Stratifizierte Auswahl: Hierbei wird die Grundgesamtheit in Untergruppen (Straten) unterteilt und aus jeder Untergruppe eine Stichprobe gezogen.
– Klusterauswahl: Hierbei werden große Gruppen von Elementen (Klumpen oder Cluster) ausgewählt und die Stichprobe wird innerhalb dieser Kluster gezogen.
Es ist wichtig, dass die Stichprobenmethode sorgfältig ausgewählt wird und dass die Stichprobe ausreichend groß ist, um valide Rückschlüsse auf die Grundgesamtheit ziehen zu können. Die Genauigkeit der Ergebnisse hängt auch von der Qualität der Datenerhebung und der Analyse ab.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn





