Population and samples explained
A population is a set of objects of interest about which one wishes to make certain statements. A sample is a subset of the population that is selected to make statements about the population. The sample is used to make estimates about the characteristics of the population.
The size of the sample depends on the size of the population and on the precision that one wants to achieve. Usually, the sample is chosen to be representative of the population so that the results are generalizable to the population.
What is a representative sample?
A representative sample is a sample that reflects the characteristics of the population. This means that the sample is composed similarly to the population in terms of the most important characteristics.
A representative sample can be selected in a number of ways, for example, by random selection or by systematic sampling. It is important that the sample is truly randomly selected from the population to ensure that it is truly representative.
A non-representative sample, on the other hand, can lead to bias and distort the results because it does not reflect the characteristics of the population.
Sampling relationship
Statistics is about making statements about a specific set of objects, called the population. The population can be very large, and it is often not possible or practical to examine all elements of the population. Instead, one selects a subset of the population, called the sample, and examines it.
The sample is used to make estimates about the characteristics of the population. It is important that the sample be representative of the population, that is, that it reflect the characteristics of the population. In this way, the results can be applied to the population.
The sampling relationship describes the relationship between the sample and the population. To understand the sampling relationship, one must realize that the sample is only a subset of the population and that the results obtained from the sample apply only to the sample. However, the results can be applied to the population if the sample is representative.
Forms of the sample survey
There are several methods of sample collection, which differ in the way the sample is selected:
- Random selection: In this method, all elements of the population are included in the sample on an equal basis. This method is the most transparent and fair, as each element has an equal chance of being included in the sample. However, random selection is not always the best method as it can sometimes result in very uneven samples.
- Stratified selection: This involves dividing the population into subgroups (strata) and drawing a sample from each subgroup. This method is used when certain characteristics or traits should be well represented in the sample. For example, in a survey of political attitudes, age strata might be used to ensure that all age strata are well represented.
- Cluster selection: In this method, large groups of items (clumps or clusters) are selected and the sample is drawn within these clusters. This method is used when the elements of the population are in natural groups, for example, schools or communities. Cluster selection is usually less expensive than the other methods, but it can result in uneven samples and is less accurate than random selection.
There are also other methods of sampling, such as the quota method or the coercive method, but these are less common and less reliable than the methods mentioned above. It is important that the appropriate sampling method is carefully selected and that the sample is sufficiently large to allow valid conclusions to be drawn about the population.
Differences in notation between sample and population
| Spellings | Sample | Population |
|---|---|---|
| Letters used | Latin letters | Greek letters |
| Quantity | N, n | N |
| Mean value | M | μ |
| Standard deviation | SD, s | σ |
Determine the size of the sample
The sample size is the size of the sample, i.e. the number of elements in the sample. There are several factors that must be considered when determining the sample size.
One of the most important factors is the size of the population. As a rule, the larger the population, the larger the sample should be in order to achieve sufficient accuracy.
Furthermore, the desired precision of the estimates plays a role in determining the sample size. As a rule, the greater the desired precision, the larger the sample size must be.
There are several formulas and tables that can be used to determine sample size based on various factors such as the size of the population, the desired precision, and the variance of the characteristics of the population. A statistician or expert in the field can assist in determining the sample size.
Calculate sample size
The sample size can be calculated using the z-value, the distribution of the population and the margin of error.
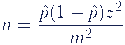
- n = sample size
- z = the z-value indicates how many standard deviations an estimate may be away from the true population for the results to be considered acceptable. The larger the z-value, the larger the sample must be to achieve sufficient precision.
- p̂ = The distribution of the population also plays a role in determining the sample size. If the population has a normally distributed or symmetrical distribution, one can use the z-value to calculate the sample size. However, if the distribution is not normally distributed or symmetrical, other methods must be used to determine the sample size.
- m =The margin of error indicates how accurate the estimates should be. The larger the margin of error, the larger the sample size can be because less precision is required. The smaller the margin of error, the larger the sample must be to achieve the desired accuracy.
To calculate the sample size, these factors are used in a formula based on the confidence interval for the estimate.
Standard error for samples
The standard error is a measure of how much the sample differs from the population. It indicates how accurate the estimates based on the sample are and how much they can deviate from the actual values in the population.
The standard error is calculated from the standard deviation of the sample and indicates how much the values in the sample differ from each other. The larger the standard error, the greater the uncertainty in the estimates and the less accurate they are.
The standard error is important because it can be used to calculate confidence intervals for estimates. Confidence intervals indicate the probability that the true value in the population is within a certain range around the estimated value. The smaller the standard error, the narrower the confidence interval and the more accurate the estimates.
It is important to note that the standard error is only a measure of the uncertainty in the estimates due to the sample and does not account for uncertainty due to other factors affecting the population. Therefore, it is important that the sample be representative of the population to ensure that the standard error is a meaningful measure of the uncertainty in the estimates.
Full survey or random sampling?
A full survey is a type of survey in which all elements of a defined population are surveyed. This means that no elements of the population are excluded and all elements have an equal chance of being included in the survey. A full survey provides a more accurate and reliable representation of the opinions, attitudes, or characteristics of the population because all elements of the population are included in the survey. However, a full survey is usually more expensive and time-consuming than a sample.
A sample is a type of survey in which only a subset of the population is surveyed. This means that some elements of the population are excluded and not all elements have an equal chance of being included in the survey. A sample is usually cheaper and faster than a full survey because only a subset of the population is surveyed. However, the sample may be less accurate and reliable because not all elements of the population are included, and there is a possibility that the sample is not representative of the entire population.
The advantages of a random sample over a full survey
- Cost: Samples are usually cheaper than full surveys because only a subset of the population is surveyed.
- Time: Samples are faster than full surveys because only a subset of the population is surveyed.
- Flexibility: random samples offer more flexibility in choosing which items to include in the survey.
- Precision: with the right sampling method and a large enough sample, the precision of a sample can match that of a full survey.
- Representativeness: With the right sampling method and sufficiently large sample, a sample can be as representative of the population as a full survey.
Frequently asked questions and answers: Sampling
What is the population?
The population is the complete population of interest for a particular study. It includes all elements of the population that have certain characteristics or attributes that are relevant to the study. The population is the main object of study and forms the basis for sample selection or for a complete survey. It is also referred to as the universe. The size of the universe can vary widely and depends on the nature of the study and the study area. For example, it may include all people in a country or all customers of a company. It is important that the universe is clearly defined and described so that the results of the study can be generalized to the population.
What is a sample?
A sample is a type of survey in which only a subset of the population is surveyed. This means that some elements of the population are excluded and not all elements have an equal chance of being included in the survey. A sample is used to draw conclusions about the opinions, attitudes, or characteristics of the entire population.
The size of the sample depends on the size of the population and the desired level of precision. The larger the sample, the more accurate and reliable the results tend to be. However, the size of the sample is also limited by the amount of time and money available. It is important that the sample is representative of the population in order to draw valid conclusions.
How to infer the population from the sample?
In order to be able to infer the population from the sample, the sample must be representative of the population. Representativeness means that the sample reflects the most important characteristics and properties of the population. If the sample is representative, the results of the sample can be generalized to the population.
There are several methods to obtain a representative sample, for example:
– Random selection: In this method, all elements of the population are equally included in the sample.
Stratified selection: Here, the population is divided into subgroups (strata) and a sample is drawn from each subgroup.
– Cluster selection: Here, large groups of elements (clumps or clusters) are selected and the sample is drawn within these clusters.
It is important that the sampling method is chosen carefully and that the sample is large enough to make valid inferences about the population. The accuracy of the results also depends on the quality of the data collection and analysis.

About me: Dr. Peter Merdian
Expert for Neuromarketing, Statistics and Data Science
Hi, I’m Peter Merdian and Statistic Hero is my heart project to help people get started with statistics easily. I hope you like the tutorials and find useful information! I myself have a PhD in Neuromarketing and love data-driven analysis. Especially with complex numbers. I know from my own experience all the problems you have as a student in your studies. That’s why the instructions are as practical and simple as possible. Feel free to use the instructions with your own data sets and calculate exciting results. I wish you success in your studies, research or work. Want to give me feedback or reach me? Dr. Peter Merdian LInkedIn





