Was ist die Faktorenanalyse?
Die Faktorenanalyse (auch Faktoranalyse oder Hauptkomponentenanalyse genannt) ist eine multivariate Analysemethode, die verwendet wird, um die Struktur von Beziehungen zwischen Variablen zu erkunden und zu erklären. Sie wird häufig in der Psychologie und in sozialwissenschaftlichen Disziplinen angewendet, um die Dimensionen oder Faktoren zu identifizieren, die die Beziehungen zwischen Variablen erklären. In diesem Beitrag werden wir uns damit beschäftigen, wie man in SPSS eine Faktorenanalyse durchführt und welche Möglichkeiten es gibt, die Faktoren zu extrahieren. Wir werden uns auch damit beschäftigen, wie man die Ergebnisse interpretiert und welche Faktoren wichtig sind, wenn man die Güte der Faktorenanalyse beurteilt.
Wenn immer Daten erhoben werden, gibt es das Problem, dass viele Variablen miteinander korrelieren. Dieser Umstand für bei Methoden wie der Regression zu Problemen weshalb mehrere Variablen, die eine ähnliche Information besitzen als Faktoren (auch Komponente genannt) zusammengefasst werden. Stark miteinander korrelierende Variablen werden in einem Faktor zusammengefasst. Das Ziel ist es, eine Variable zu erschaffen, die möglichst denselben Informationsgehalt von mehreren Beinhaltet. Der Schwierigkeit liegt dabei. Die Daten so weit wie möglich zu reduzieren und dabei so wenig Informationen wie möglich zu verlieren. In SPSS befindet sich diese Methode als Dimensionsreduzierung.
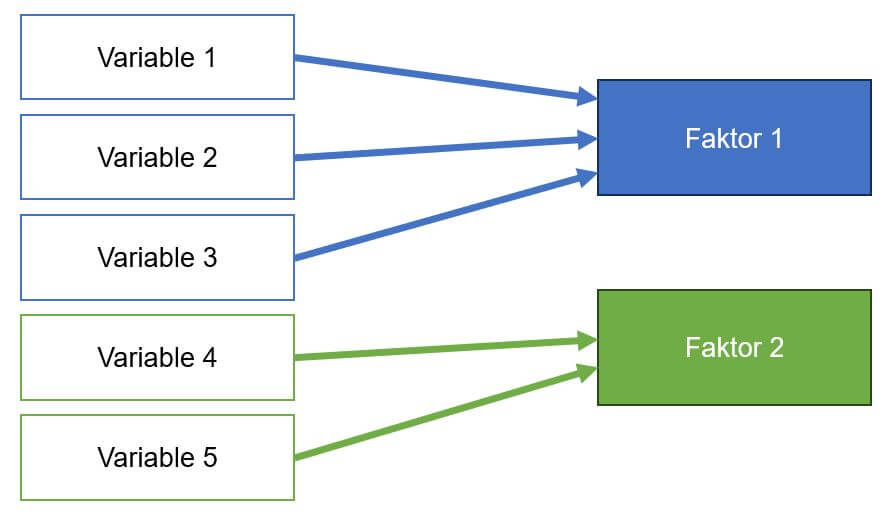
Die Faktoranalyse ist ein multivariates Verfahren, dass berechnet, wie stark jede Variable auf einen theoretischen Faktor lädt. Je stärker die Ladung einer Variable, desto höher ist die Gewichtung mit dem theoretischen Faktor. Das bedeutet, dass sie ähnliche Informationen teilen. Diese Zusammenfassung von Variablen (Items) ist rein mathematisch. Achte dabei, dass die Zusammenführung einen inhaltlichen Sinn ergeben.
Faktoren fassen mehrere Variablen zusammen, um so die wichtigsten Informationen des Datensatzes zu extrahieren. Das Ergebnis sind wenige Hauptkomponenten (Faktoren) die eine größere Varianz im Datensatz erklären können.
Wo finde ich die Beispieldaten für diese Anleitung
Die Beispieldaten gibt es hier: Beispieldaten
Voraussetzungen
- LinearitätLinearität Linearität bezieht sich auf die Beziehung zwischen zwei oder mehr Variablen, die durch eine gerade Linie dargestellt wird, bei der die Veränderung einer Variablen direkt proportional zur Veränderung der anderen Variable ist. prüfen: Linearität sollte gegeben sein. Eine Anleitung zur Prüfung der Linearität befindet sich hier.
- AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind. prüfen: Ausreißer sind Werte, die im ungewöhnlich klein oder groß sind und einen negativen Einfluss auf die Analyse haben, weil sie die Ergebnisse verfälschen. Je weniger Ausreißer ein Datensatz hat, desto besser. Eine Anleitung zur Prüfung der statistischen Ausreißer befindet sich hier.
- NormalverteilungNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. : Die Variablen sollten normalverteilt sein. Eine Anleitung zum Überprüfen befindet sich hier.
- Stetigkeit: Es wird eine stetige Beziehung der Variablen vorausgesetzt.
- SkalenniveauSkalenniveau Das Skalenniveau bezieht sich auf den Typ von Daten, der in einer Studie erhoben wurde, und gibt an, wie die Daten in Bezug auf die Messbarkeit und die Möglichkeit zur Verwendung von Statistiken kodifiziert sind.: Intervallskalierte Variablen sind notwendig. Anleitung Skalenniveaus.
- Anzahl an Fällen: Stichprobengröße. a. 4 bis 20 Fälle pro berechneter variable. Eine Hauptkomponentenanalyse mit 5 Variablen würde 20 bis 100 Probanden benötigen. Als Daumenregel: es sollten fällte bzw. 10 Pro Variable sein, alles unter 100 Probanden insgesamt sollte kritisch hinterfragt werden.
Exkurs: Die Rotationsverfahren erklärt
Varimax verstärkt die Ladungen und vereinfacht die Zuordnung der Variablen Dadurch sind große Ladungen vergrößert und kleine Ladungen verkleinert.
Quartimax: Ähnelt Varimax mit dem Unterschied, dass eine Variable eher auf einen Faktor ladet.
Equamax (bzw. Equimax) ist ein Kompromiss aus Quartimax und Varimax. Faktoren werden voneinander abgegrenzt während Ladungen betont werden.
Promax ist ein schiefwinkliges Verfharen: Zunächst wird eine Varimaxrotation durchgeführt, bei der die Faktorladungen erneut potenziert werden. Dadurch werden große Effekte noch größer und kleine Effekte noch kleiner, was die Interpretierbarkeit vereinfacht.

Durchführung der Faktorenanalyse in SPSS
Hauptkomponentenanalyse in SPSS berechnen (Faktorenanalyse)
Auswahl im Menü

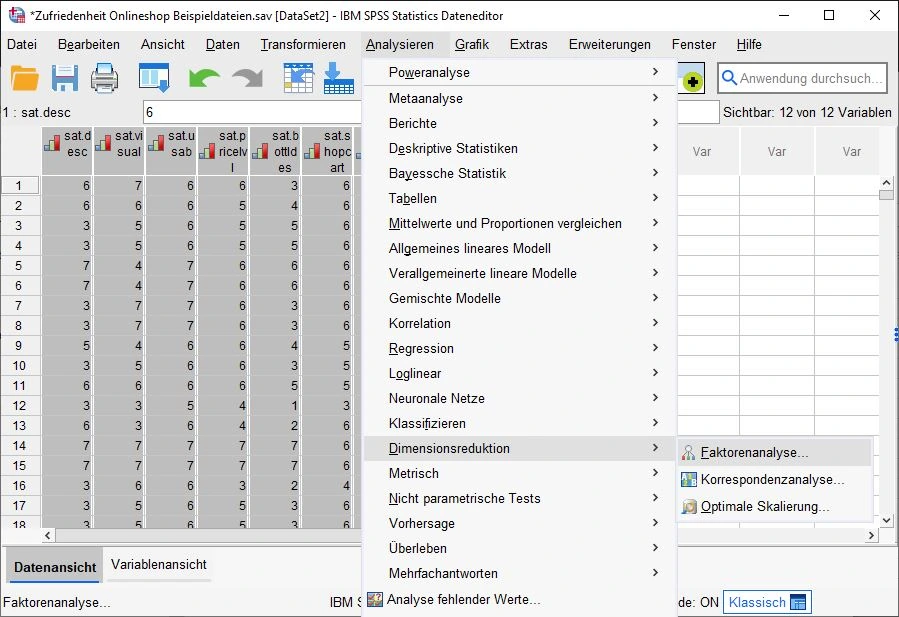
Wir klicken auf der Benutzeroberfläche auf Analysieren > Dimensionsreduktion > Faktorenanalyse…
Auswahl der Daten

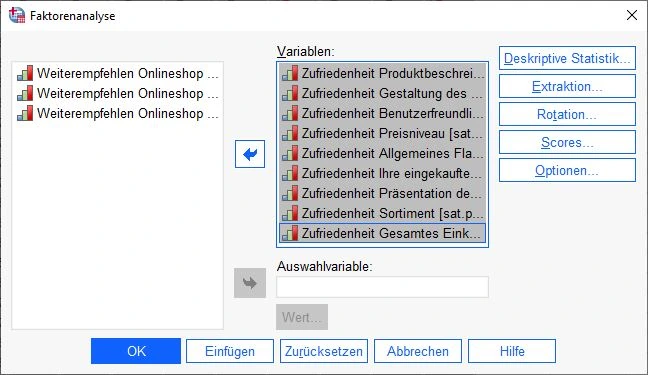
Im Dialogfenster ziehen sehen wir zwei Spalten. Links werden alle Variablen angezeigt, die im Datensatz zur Verfügung stehen. Wir wählen die Variablen für die Hauptkomponentenanalyse aus und ziehen sie auf die rechte Spalte (Variablen).
Wenn alle ausgewählten Variablen im rechten Feld sind, beginnen wir die Hauptkomponentenanalyse anzupassen.
Als Nächstes klicken wir auf die Schaltfläche Deskriptive Statistik.
Deskriptive Statistiken für die Faktorenanalyse auswählen

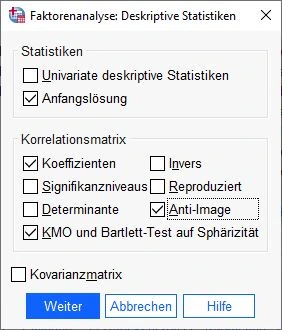
Im Dialogfenster wählen wir im Feld Statistik die Option Anfangslösung. Im Feld Korrelationsmatrix setzen wir Häkchen bei Koeffizienten, Anti-Image, KMO und Bartlett-Test auf Sphärizität.
Anschließend bestätigen wir die Eingaben mit einem Klick auf Weiter.
Auswahl der Extraktion

Im nächsten Schritt wählen wir Extraktion auf der rechten Seite des Dialogfensters.
Extraktion bestimmen

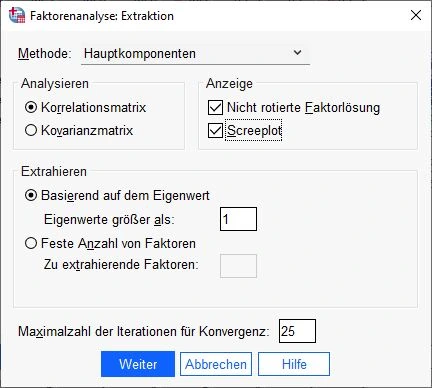
Als Methoden wählen wir Hauptkomponenten. Im Feld Analysieren währen wir Korrelationsmatrix und bei Anzeige die Optionen Nicht rotierte Faktorlösung und Screeplot. Alle anderen Einstellungen sollten wie auf dem Bildschirmausschnitt unten sein (Standardeinstellung).
Mit einem Klick auf Weiter bestätigen wir die Eingaben.
Auswahl der Extraktion

Als Nächstes klicken wir auf Rotation.
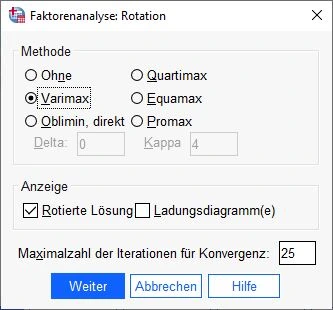
In diesem Dialogfenster wählen wir eine Rotationsmethode. Die gängigste Methode ist Varimax. Im Feld Anzeige wählen wir die Schaltfläche Rotierte Lösung und klicken auf Weiter.
Auswahl der Optionen

Als nächstes wählen wir die Schaltfläche Optionen auf der rechten Seite.
Optionen der Hauptkomponentenanalyse bestimmen

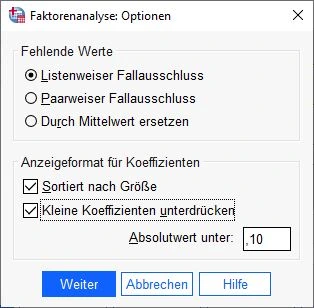
Im Feld Anzeigeformat für Koeffizienten setzen wir einen Haken auf Sortiert nach Größe, Kleine Koeffizeinten unterdrücken. Absolutwert unter sollte ,10. Anschließend wird auf Weiter geklickt.
Bereit zum Start

Das war es mit den Einstellungen. Ein Klick auf OK startet die Berechnung der Hauptkomponentenanalyse.
Interpretation der Hauptkomponetnenanalyseergebnisse
Korrelationstabellen
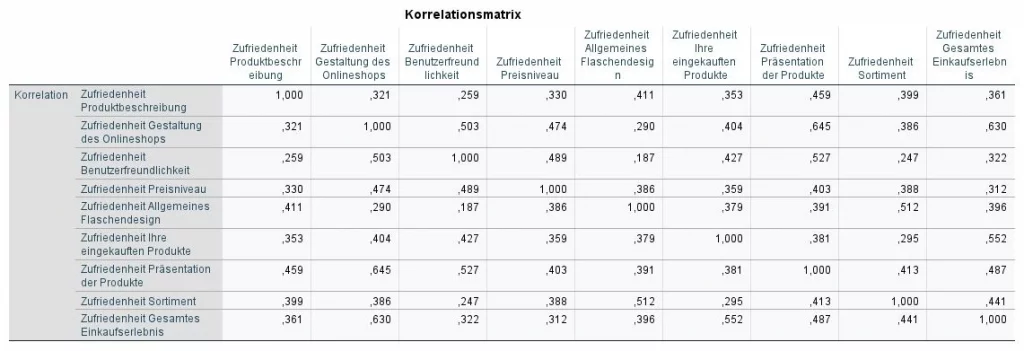
So umfangreich die Eingaben beim Konfigurieren der Hauptkomponentenanalyse war, so umfangreich fallen die Auswertungen an. Zunächst blicken wir auf die Korrelationsmatrix-Tabelle. Diese Tabelle zeigt uns die jeweiligen KorrelationenKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird. zwischen den Variablen. Weil die Variablen eines Faktors korrelieren sollten, überprüfen wir hier, ob es Variablen gibt, die keine KorrelationKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird. mit anderen Variablen haben (mindestens .30). Solche Variablen sollten entfernt werden, damit die gesamte Analyse entfernt wird. Weiter möchten wir keine Variablen, die mehr als .90 korrelieren. Hier sind die Informationen zu ähnlich und es besteht die Gefahr einer Multikollinearität.
KMO Kriterium und Test auf Sphärizität
Eine der wichtigsten Ausgaben ist das Kaiser-Meyer-Olkin-Kriterium. Das KMO-Kriterium ist die wichtigste Kriterium zur Bestimmung der Qualität der Berechnung. Der Wert darf niemals das Minimum von .50 unterschreiten. Der größte theoretische Wert ist 1.00.
Das zweite wichtige Kriterium ist der Bartlett-Test auf Sphärizität, der eine Beziehung zwischen den Variablen bestätigt. Um die Hauptkomponentenanalyse fortzufahren, muss die Signifikanz nach Bartlett signifikant sein, d. h. P-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. ist mindestens p<.05.

Zusammenfassung
KMO-Wert sollte mindestens .50 sein und die Signifikanz des Bartlett´s Test auf Sphärizität p=.05 oder niedriger sein. Falls dies nicht zutrifft sollte die Berechnung abgebrochen werden.
In unserem Beispiel ist der KMO-Wert=.83 und Bartlett´s Test auf Sphärizität hochsignifikant (p<.001). Wir können mit der Hauptkomponentenanalyse fortfahren.
Anti-Image-Matrizen
Das KMO Kriterium analysiert die Beziehung aller Variablen. Die Anti-Image-Matrizen gibt uns eine ähnliche Auskunft für einzelne Variablen. Auch hier gilt, dass alle Variablen einen Wert von mindestens .50 haben sollten, siehe rotmarkierte Bereiche im Bildschirmausschnitt. In unserem Beispiel erfüllen alle Variablen ähnliche Werte wie der KMO-Wert (.83)
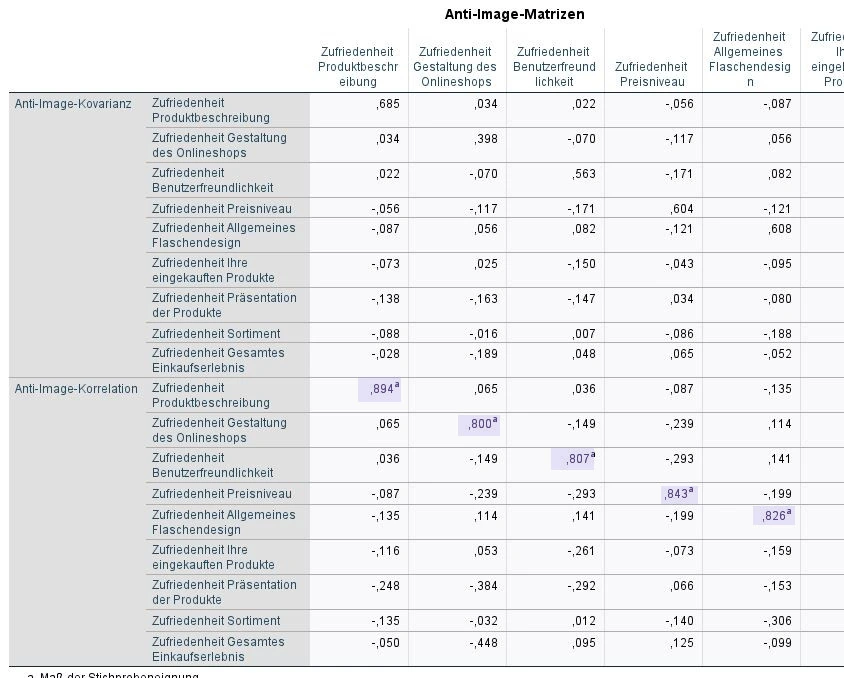
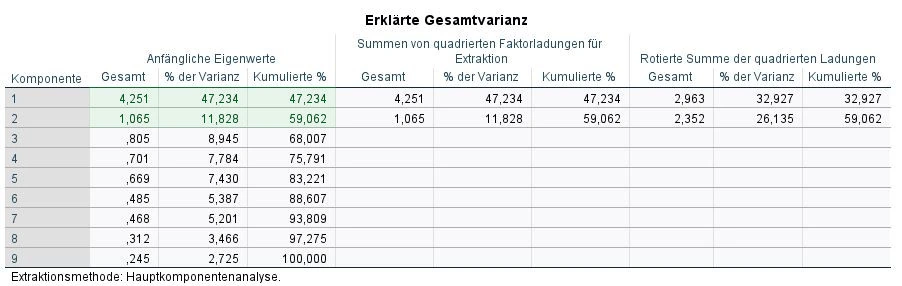
Tabelle “Erklärte Gesamtvarianz”
Die Statistiksoftware SPSS ist bei der Erstellung von Faktoren großzügig. Es erstellt stets so viele Faktoren wie es Variablen gibt. Anhand dieser Tablle entscheiden wir, inwieweit die 9 Variablen in wenigen Faktoren zusammengefasst werden kann.
Wir blicken auf die Spalte “anfänglichen Eigenwerte (Initial Eigenvalues)” und dort auf “Total”. Wir nehmen nur Faktoren die Eigenwerte von mindestens 1.00 haben. Zwei Komponenten erfüllen dieses Kriterium. D.h. die Anzahl der Komponenten kann auf zwei festgelegt werden.
Darüber hinaus zeigt die Tabelle, dass der erste Faktor 47.23% der Gesamtvarianz erklären kann. Beide Faktoren zusammen (cullative %) erklären zusammen 59.06% der Gesamtvarianz, was ein Informationsverlust von 40% steht.
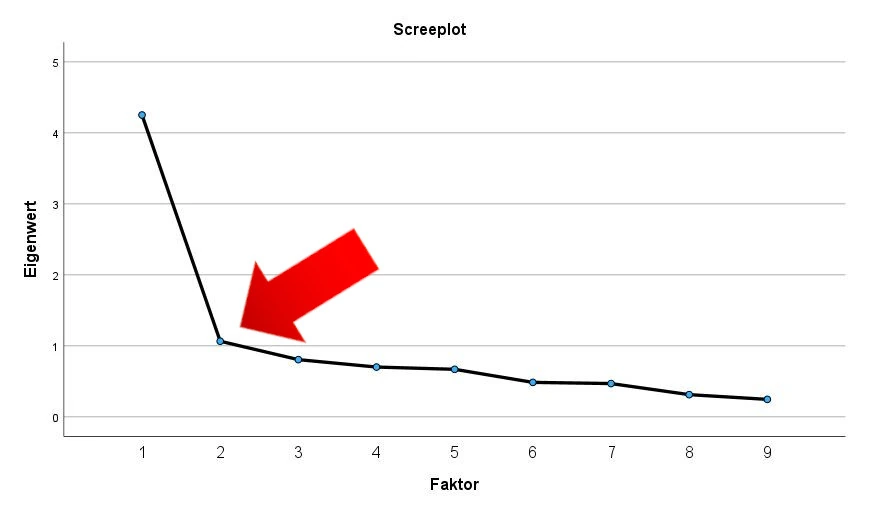
Die Bestimmung der Anzahl der Faktoren kann ebenfalls mit einem ScreePlot bestimmt werden. Der Punkt, andem der sogenannte “Ellenbogen” aufsetzt, zeigt uns die Anzahl der Faktoren. In unserem Beispiel 2.
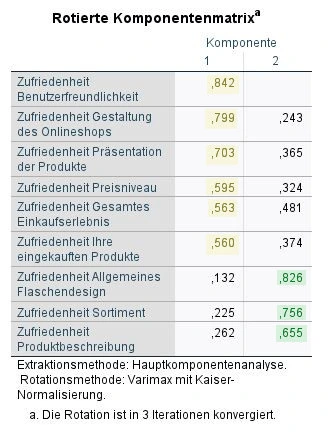
Rotierte Komponentenmatrix
Die rotierte Komponentenmatrix ist das Herz der Hauptkomponentenanalyse. Die Spalten Komponente 1 und 2 zeigt die jeweilige Ladung der einzelnen Variable auf eine der beiden Komponenten. Durch die Varimaxrotation wurden die Ladungen deutlicher. Sie können einen Wert von 1 bis -1 sein. Manche Variablen laden auf beiden Komponenten; in diesem Fall ordnen wir eine Variable der stärksten Ladung zu.
Bei der Analyse unseres Datensatzes laden die ersten sechs Variablen auf die erste Komponente. Die letzten drei Variablen laden auf den Faktor 2.
Hinweis: Vergleiche die rotierte Komponentenmatrix mit der nicht rotierten Martrix, um die Unterschiede zu sehen.
Wie geht es weiter?
Unsere Analysen haben uns gezeigt, dass wir aus unseren ursprünglich 9 Variablen zwei Faktoren bilden können. Das heißt, dass wir mit zwei Variablen im Grunde eine ausreichend hohe Aussagekraft wie mit 9 Variablen haben. Im nächsten Schritt müssen wir diese Faktoren selbständig erstellen. Hier nimmt uns SPSS leider die Arbeit nicht ab. Im letzten Teil dieser Einleitung erfährst du, wie du die erste Dimension erstellen kannst.
Erstellung neuer Variablen
Auswahl im Menü
Im Menü wählen wir oben: Transformieren > Variable berechnen
Variable in SPSS berechnen
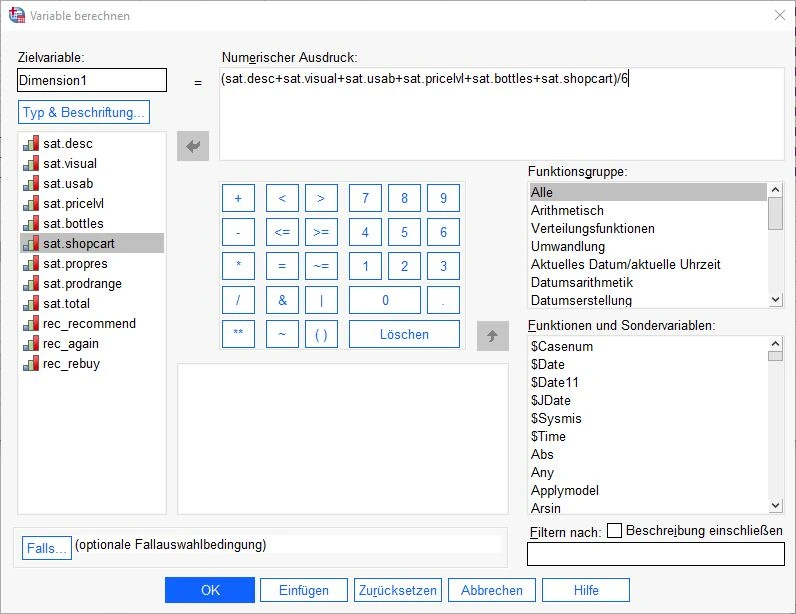
Es öffnet sich das Dialogfenster “Variable berechnen”.
Zunächst geben wir im Feld Zielvariable oben links den Namen der neuen Variable ein (Beispielsweise Dimension 1). Anschließend ziehen wir von der linken Spalte die erste Variable in das Feld Numerischer Ausdruck. Anschließend drücken wir auf der Tastatur die Plus-Taste (+). Als Nächstes ziehen wir die nächste Variable des ersten Faktors in das Feld numerischer Ausdruck und drücken wieder die Plus-Taste. Das wiederholen wir, bis wir alle Variablen des Faktors als Summe im Feld haben (siehe Bildschrimausschnitt).
Nachdem alle Variablen im Feld Numerischer Ausdruck als Addition aufgefasst werden, klammern das Gesamtergebnis ein. Anschließend dividieren wir die Gesamtsumme durch die Anzahl der verwendeten Variablen unserer Gleichung. In unserem Fall verwenden wir 6 Variablen, demnach dividieren wir durch 6. Unser neuer Faktor soll nicht die Summe, sondern das arithmetische Mittel der inkludierten Variablen beinhalten.
Anschließend bestätigen wir die Eingaben und klicken auf OK.
Neue Variable im Datensatz
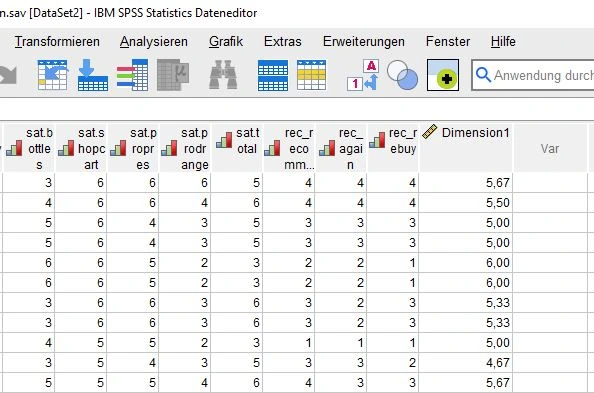
In der Datenansicht sehen wir die neue Variable “Dimension1”, der die ersten sechs Variablen zusammenfasst.
Weitere Schritte
In unserem Beispiel haben wir neun Variable, zwei Faktoren gebildet. Beide Faktoren sind ein Versuch, ein theoretisches Konstrukt hinsichtlich die Zufriedenheit auf dem Onlineshop zu messen. Eine notwendige Voraussetzung für dieses Messinstrument ist die Reliabilität. Aus diesem Grund sollten wir im nächsten Schritt eine Rentabilitätsanalyse durchführen. Hier geht es zur Anleitung Reliabilitäts (Analyse Cronbach´s Alpha).
Fazit zum Thema Hauptkomponentenanalyse in SPSS
Insgesamt ist die Faktorenanalyse bzw. Hauptkomponentenanalyse ein mächtiges Analysewerkzeug, das in vielen Disziplinen eingesetzt wird, um die Struktur von Beziehungen zwischen Variablen zu erkunden und zu erklären. Sie kann sowohl explorative als auch konfirmative Zwecke haben und es gibt verschiedene Methoden, die verwendet werden können, um die Faktoren zu extrahieren. Es ist wichtig, dass man die Güte der Faktorenanalyse beurteilt und sicherstellt, dass sie valide und reliabel ist, bevor man die Ergebnisse interpretiert und auf die Daten anwendet. Wenn man sorgfältig und kritisch die Faktorenanalyse anwendet, kann sie ein nützliches Werkzeug sein, um die Struktur von Beziehungen zwischen Variablen zu verstehen und zu erklären.
5 Fakten zur Faktorenanalyse in SPSS
- Die Faktorenanalyse ist eine multivariate Analysemethode, die verwendet wird, um die Struktur von Beziehungen zwischen Variablen zu erkunden. Sie dient dazu, die Ursache-Wirkungs-Beziehungen zwischen Variablen zu untersuchen und zu erklären.
- Die Faktorenanalyse wird häufig in der Psychologie und in sozialwissenschaftlichen Disziplinen angewendet, um die Dimensionen oder Faktoren zu erkennen, die die Beziehungen zwischen Variablen erklären.
- Die Faktorenanalyse kann sowohl explorative als auch konfirmative Zwecke haben. Die explorative Faktorenanalyse wird verwendet, um neue Strukturen oder Faktoren zu entdecken, während die konfirmative Faktorenanalyse dazu dient, bereits bekannte Strukturen oder Faktoren zu bestätigen.
- In der Faktorenanalyse werden die Beziehungen zwischen Variablen mithilfe von Eigenvektoren und Eigenwerten modelliert. Eigenvektoren sind Vektoren, die die Struktur der Beziehungen zwischen Variablen beschreiben, während Eigenwerte die Stärke dieser Beziehungen angeben.
- Die Faktorenanalyse ist eine flexibles Analysewerkzeug und es gibt verschiedene Methoden, die verwendet werden können, um die Faktoren zu extrahieren, darunter die Hauptkomponentenanalyse und die Varimax-Rotation. Die Wahl der geeigneten Methode hängt von den Zielen und den Eigenschaften der Daten ab.
Häufig gestellte Fragen und Antworten: Hauptkomponentenanalyse und Faktorenanalyse in SPSS
Was ist das Ziel der Faktorenanalyse?
Das Ziel der Faktorenanalyse ist es, eine große Anzahl von Variablen auf weniger Variablen zusammenzufassen, die die wichtigsten Merkmale der Daten beschreiben. Diese zusammengefassten Variablen werden als Faktoren bezeichnet und können verwendet werden, um die Struktur der Daten zu verstehen und Vorhersagen über die Daten zu treffen.
Die Faktorenanalyse kann verwendet werden, um die Dimensionen oder Merkmale der Daten zu reduzieren und zu verstehen, wie die Variablen miteinander in Beziehung stehen. Sie kann auch verwendet werden, um redundante Informationen zu eliminieren und die Analyse von Daten mit vielen Variablen zu vereinfachen.
Insgesamt ist das Ziel der Faktorenanalyse, die Struktur der Daten zu erkennen und zu verstehen, indem man die wichtigsten Merkmale der Daten identifiziert und zusammenfasst. Sie wird häufig in vielen Bereichen wie der Psychologie, der Marketingforschung und der Sozialwissenschaften eingesetzt.
Wie funktioniert eine Faktorenanalyse (Hauptkomponentenanalyse)?
Die Faktorenanalyse ist eine statistische Methode, die verwendet wird, um eine große Anzahl von Variablen auf weniger Variablen zusammenzufassen, die die wichtigsten Merkmale der Daten beschreiben. Diese zusammengefassten Variablen werden als Faktoren bezeichnet.
Die Faktorenanalyse wird in mehreren Schritten durchgeführt:
– Vorverarbeitung: Die Daten werden geprüft, um sicherzustellen, dass sie für die Analyse geeignet sind. Dazu gehört, dass die Daten vollständig und konsistent sind und dass keine Ausreißer oder fehlerhafte Werte vorliegen.
– Faktorensuche: Die Korrelationen zwischen den Variablen werden berechnet und eine Korrelationsmatrix erstellt. Dann wird eine Faktorenmethode verwendet, um die Faktoren zu identifizieren, die die Korrelationen der Variablen am besten beschreiben. Es gibt verschiedene Faktorenmethoden, die man verwenden kann, wie zum Beispiel die Hauptkomponentenanalyse oder die Rotationsmethoden.
– Faktorenschätzung: Nachdem die Faktoren identifiziert wurden, werden Schätzungen für die Faktorenwerte für jeden Fall berechnet. Diese Faktorenwerte können verwendet werden, um Vorhersagen über die Daten zu treffen.
– Faktoreninterpretation: Die Faktoren werden interpretiert, um zu verstehen, was sie bedeuten und wie sie die Variablen beeinflussen. Man kann auch die Reliabilität und Validität der Faktoren überprüfen, um sicherzustellen, dass sie gut beschreiben, was sie sollen.
Insgesamt ist die Faktorenanalyse eine nützliche Methode zur Verringerung der Komplexität von Daten mit vielen Variablen und zur Erkennung der wichtigsten Merkmale der Daten. Sie wird häufig in vielen Bereichen wie der Psychologie, der Marketingforschung und der Sozialwissenschaften eingesetzt.
Wann ist eine Hauptkomponentenanalyse PCA sinnvoll?
Eine Hauptkomponentenanalyse (PCA) ist eine statistische Methode, die verwendet wird, um eine große Anzahl von Variablen auf weniger Variablen zusammenzufassen, die die wichtigsten Merkmale der Daten beschreiben. Diese zusammengefassten Variablen werden als Hauptkomponenten bezeichnet.
Die Hauptkomponentenanalyse ist sinnvoll, wenn man versucht, die Struktur von Daten mit vielen Variablen zu verstehen und zu reduzieren. Sie kann verwendet werden, um die Dimensionen oder Merkmale der Daten zu reduzieren und zu verstehen, wie die Variablen miteinander in Beziehung stehen. Sie kann auch verwendet werden, um redundante Informationen zu eliminieren und die Analyse von Daten mit vielen Variablen zu vereinfachen.
Für welche Fragestellungen werden Faktorenanalysen genutzt?
Faktorenanalysen werden in vielen Bereichen genutzt, in denen man versucht, die Struktur von Daten mit vielen Variablen zu verstehen und zu reduzieren. Sie können in vielen verschiedenen Bereichen eingesetzt werden, einschließlich:
– Psychologie: Faktorenanalysen werden häufig in der Psychologie verwendet, um die Dimensionen von Persönlichkeitsmerkmalen oder anderen psychologischen Konstrukten zu untersuchen.
– Marketingforschung: Faktorenanalysen können verwendet werden, um die Struktur von Kundenbefragungen zu verstehen und um herauszufinden, welche Faktoren die Einstellungen und Verhaltensweisen von Kunden am besten beschreiben.
– Sozialwissenschaften: Faktorenanalysen werden häufig in den Sozialwissenschaften eingesetzt, um die Struktur von sozialen Phänomenen zu verstehen und um Vorhersagen über soziale Ergebnisse zu treffen.
Wie viele Items pro Faktor?
Es gibt keine feste Regel dafür, wie viele Items pro Faktor in einer Faktorenanalyse enthalten sein sollten. Die Anzahl der Items pro Faktor hängt von den spezifischen Eigenschaften der Daten und der Fragestellung ab.
Eine allgemeine Empfehlung ist, dass jeder Faktor mindestens drei bis vier Items enthalten sollte, um eine ausreichende Schätzung der Faktorenwerte zu gewährleisten. Eine zu geringe Anzahl von Items pro Faktor könnte dazu führen, dass die Schätzungen der Faktorenwerte zu unsicher sind und dass die Ergebnisse der Analyse weniger valide sind.
Es gibt jedoch keine Obergrenze für die Anzahl von Items pro Faktor. In manchen Fällen kann es sinnvoll sein, eine größere Anzahl von Items pro Faktor zu haben, um eine bessere Schätzung der Faktorenwerte zu erhalten. Es ist wichtig, dass man die spezifischen Eigenschaften der Daten und die Fragestellung berücksichtigt, wenn man entscheidet, wie viele Items pro Faktor in der Analyse enthalten sein sollten.
Was ist ein Eigenwert Faktorenanalyse?
Ein Eigenwert ist ein Maß für die Variabilität, die von einem Faktor in einer Faktorenanalyse erklärt wird. Ein hoher Eigenwert bedeutet, dass der Faktor einen großen Anteil an der Variabilität der Daten erklärt, während ein niedriger Eigenwert bedeutet, dass der Faktor nur einen geringen Anteil an der Variabilität der Daten erklärt.
In der Faktorenanalyse werden Eigenwerte verwendet, um die Bedeutung der Faktoren zu beurteilen. Ein Faktor mit einem hohen Eigenwert ist in der Regel als wichtiger angesehen als ein Faktor mit einem niedrigen Eigenwert, da er einen größeren Anteil an der Variabilität der Daten erklärt.
Es ist wichtig zu beachten, dass Eigenwerte nicht direkt verglichen werden können, da sie in unterschiedlichen Einheiten gemessen werden. Stattdessen werden die Eigenwerte normalerweise als Prozentsätze der Variabilität dargestellt, die von jedem Faktor erklärt wird. Diese Prozentsätze werden als Eigenwertzerlegung bezeichnet und können verwendet werden, um die Bedeutung der Faktoren in Bezug auf die Gesamtvariabilität der Daten zu beurteilen.
Was ist eine explorative Faktorenanalyse?
Eine explorative Faktorenanalyse ist eine Art von Faktorenanalyse, die verwendet wird, um die Struktur von Daten zu untersuchen und zu verstehen. Im Gegensatz zu einer konfirmatorischen Faktorenanalyse, bei der man versucht, ein vorher formuliertes Modell der Struktur der Daten zu testen, ist das Ziel einer explorative Faktorenanalyse, die Struktur der Daten zu entdecken und zu erkunden.
Bei einer explorative Faktorenanalyse werden die Korrelationen zwischen den Variablen berechnet und eine Korrelationsmatrix erstellt. Dann wird eine Faktorenmethode verwendet, um die Faktoren zu identifizieren, die die Korrelationen der Variablen am besten beschreiben. Es gibt verschiedene Faktorenmethoden, die man verwenden kann, wie zum Beispiel die Hauptkomponentenanalyse oder die Rotationsmethoden.
Nachdem die Faktoren identifiziert wurden, werden Schätzungen für die Faktorenwerte für jeden Fall berechnet. Diese Faktorenwerte können verwendet werden, um Vorhersagen über die Daten zu treffen. Die Faktoren werden dann interpretiert, um zu verstehen, was sie bedeuten und wie sie die Variablen beeinflussen.
Insgesamt ist die explorative Faktorenanalyse eine nützliche Methode zur Erkundung und Verstehen der Struktur von Daten mit vielen Variablen. Sie wird häufig in vielen Bereichen wie der Psychologie, der Marketingforschung und der Sozialwissenschaften eingesetzt.
Warum Rotation bei Faktorenanalyse?
Rotation bei einer Faktorenanalyse ist ein Verfahren, bei dem die Faktoren so gedreht werden, dass sie möglichst viel Unterschiedlichkeit zwischen den Items zeigen. Die Rotation kann dazu beitragen, die Struktur der Daten besser zu verstehen und die Faktoren leichter interpretierbar zu machen.
Es gibt verschiedene Arten von Rotationen, die man in einer Faktorenanalyse verwenden kann, wie zum Beispiel orthogonale Rotationen oder oblique Rotationen. Orthogonale Rotationen drehen die Faktoren so, dass sie völlig unabhängig voneinander sind und keine Korrelation miteinander haben. Oblique Rotationen erlauben es, dass die Faktoren miteinander korrelieren.
Die Wahl der Art der Rotation hängt von der spezifischen Fragestellung und den Eigenschaften der Daten ab. In manchen Fällen kann es sinnvoller sein, orthogonale Rotationen zu verwenden, um die Unabhängigkeit der Faktoren zu betonen, während in anderen Fällen oblique Rotationen besser geeignet sein können, um die Struktur der Daten besser zu verstehen.
Insgesamt kann die Rotation bei einer Faktorenanalyse dazu beitragen, die Struktur der Daten besser zu verstehen und die Faktoren leichter interpretierbar zu machen. Sie wird häufig in vielen Bereichen wie der Psychologie, der Marketingforschung und der Sozialwissenschaften eingesetzt.
Was sind weiterführende Links zum Thema Faktorenanalyse in SPSS?
Was ist der Faktorwert?
Der Faktorwert ist eine Schätzung des Ausmaßes, in dem eine Variable von einem Faktor in einer Faktorenanalyse beeinflusst wird. Der Faktorwert einer Variable gibt an, wie stark die Variable mit dem Faktor korreliert und wie gut sie von dem Faktor erklärt wird.
In der Faktorenanalyse werden Faktorwerte für jede Variable berechnet, indem man die Korrelation zwischen der Variable und dem Faktor misst. Ein hoher Faktorwert bedeutet, dass die Variable stark mit dem Faktor korreliert und gut von ihm erklärt wird, während ein niedriger Faktorwert bedeutet, dass die Variable schwach mit dem Faktor korreliert und weniger gut von ihm erklärt wird.
Die Faktorwerte können verwendet werden, um die Bedeutung der Variablen für den Faktor zu beurteilen und um Vorhersagen über die Variablen zu treffen. Sie können auch verwendet werden, um die Validität und Reliabilität der Faktoren zu überprüfen und um die Struktur der Daten besser zu verstehen.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn