Was ist der χ² (Chi-Quadrat) Test für Unabhängigkeit?
Der Chi-Quadrat-Test für Unabhängigkeit ist ein wichtiges statistisches Verfahren, das verwendet wird, um zu überprüfen, ob es einen Zusammenhang zwischen zwei kategorialen (nominal skalierten) Variablen gibt. Er wird häufig in der Sozialwissenschaft, Psychologie und anderen Bereichen verwendet, in denen man sich für die Beziehungen zwischen verschiedenen Merkmalen interessiert. In diesem Artikel wird beschrieben, wie man einen Chi-Quadrat-Test für Unabhängigkeit in SPSS durchführt und wie man das Ergebnis interpretiert. Zunächst wird jedoch eine kurze Einführung in die Konzepte des Chi-Quadrat-Tests für Unabhängigkeit gegeben.
Was berechnet ein Chi-Quadrat Test?
Beim Chi-Quadrat-Test wird die Chi-Quadrat-Statistik berechnet, die verwendet wird, um zu überprüfen, ob es einen signifikanten Unterschied zwischen den tatsächlichen und den erwarteten Häufigkeiten in den verschiedenen Kategorien der kategorialen Variablen gibt. Die tatsächlichen Häufigkeiten sind die Anzahl der Beobachtungen in jeder Kategorie, während die erwarteten Häufigkeiten die Anzahl der Beobachtungen sind, die man erwarten würde, wenn es keinen Zusammenhang zwischen den Variablen gäbe.
Um die Chi-Quadrat-Statistik zu berechnen, werden die Unterschiede zwischen den tatsächlichen und den erwarteten Häufigkeiten für jede Kategorie quadriert und dann durch die erwarteten Häufigkeiten geteilt. Die Quadrate dieser Unterschiede werden dann summiert, um die Chi-Quadrat-Statistik zu berechnen. Je größer die Chi-Quadrat-Statistik ist, desto größer ist der Unterschied zwischen den tatsächlichen und den erwarteten Häufigkeiten und desto wahrscheinlicher ist es, dass es einen signifikanten Unterschied zwischen den Variablen gibt.
Das Beispiel dieser Anleitung: Essgewohnheiten und Essen
Die HypotheseHypothese Eine Hypothese ist eine vorläufige Annahme über einen Zusammenhang oder ein Phänomen, die aufgrund von Beobachtungen oder vorherigen Erkenntnissen gemacht wird und überprüft werden kann, indem sie durch Forschung oder Experimente gestützt oder widerlegt wird., dass Männer mehr Steak essen als Frauen und Frauen mehr Salat essen als Männer, ist eine weit verbreitete Annahme, die in vielen Gesellschaften gemacht wird. Um zu überprüfen, ob diese Hypothese wahr ist, wurde eine Studie durchgeführt, in der die Essgewohnheiten von Männern und Frauen untersucht wurden. Ob Männer tatsächlich häufiger Steak als Frauen essen, werden wir mit unserem Beispieldatensatz überprüfen.
Wo ist der Beispieldatensatz?
Hier ist der Beispieldatensatz
Voraussetzungen Chi-Quadrat Test
- Unabhängigkeit der Messungenunabhängige Messungen Unabhängige Messungen sind Messungen, die von verschiedenen Beobachtern oder Messverfahren durchgeführt werden und die vermutlich keine Wechselwirkungen oder Verzerrungen durch die Beobachter oder Messverfahren haben. Sie werden verwendet, um die Zuverlässigkeit und Validität von Messungen und Studien zu verbessern und werden häufig in der Psychologie und Sozialwissenschaften verwendet.: Wie beim ungepaarten t-Test müssen die Variablen unabhängig voneinander sein. Die Messwerte dürfen der verschiedenen Gruppen dürfen sich nicht beeinflussen. Zum Beispiel darf eine Versuchsperson nur in einer Gruppe vertreten sein, nicht in beiden.
- SkalenniveauSkalenniveau Das Skalenniveau bezieht sich auf den Typ von Daten, der in einer Studie erhoben wurde, und gibt an, wie die Daten in Bezug auf die Messbarkeit und die Möglichkeit zur Verwendung von Statistiken kodifiziert sind.: Wir erwarten, dass unsere Variablen kategorial sind, daher ist es angemessen, sie auf einer nominalen Skala zu messen. Das gilt für beide Variablen, die Analysiert werden sollen.
- Anzahl an Fällen: Jede Zelle muss 5 oder mehr Fälle (Beobachtungen, Versuchspersonen, etc.) enthalten.
Chi-Quadrat Test in SPSS durchführen
Chi-Quadrat Test in SPSS durchführen
Auswahl im Menü

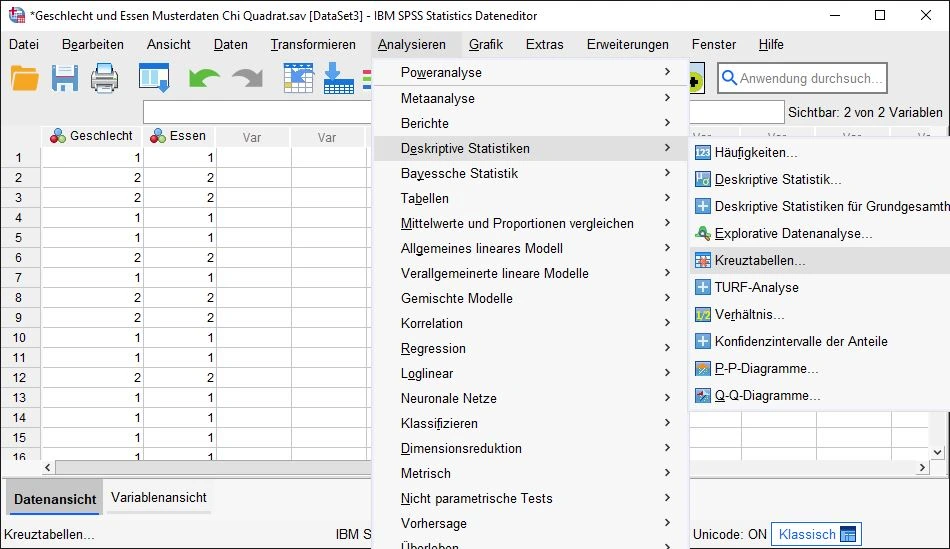
Wir wählen im Menü: Analysieren > Deskriptive Statistiken > Kreuztabellen
Kreuztabellen in SPSS

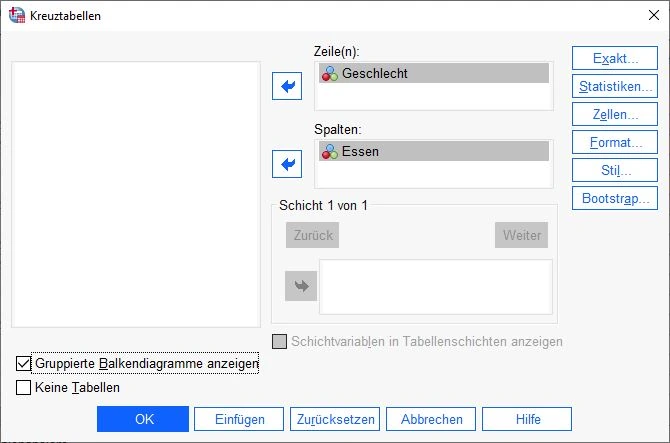
Es erscheint ein Dialogfenster mit mehreren Feldern. Links sehen wir die Auswahl der verfügbaren Variablen. Wir verschieben die Variablen auf die Felder Zeile und Spalten.
Darüber hinaus setzen wir einen Haken auf Gruppierte Balkendiagramme anzeigen weiter unten.
Anschließend klicken wir auf das Feld Statistiken auf der rechten Seite.
Statistik einstellen für Chi-Quadrat Test in SPSS

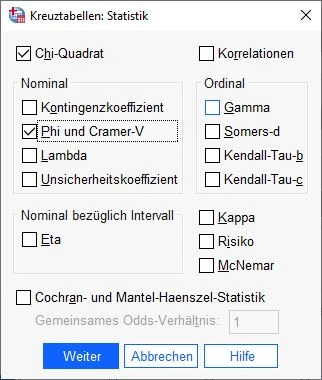
Wir wählen folgende Optionen aus:
– Chi-Quadrat
– Phi und Cramer-VAnschließend klicken wir auf Weiter.
Auswahl Zellen im Kreuztabellenfenster

Auf der rechten Seite wählen wir die Option Zellen
Auswahl: Zellen anzeigen in SPSS

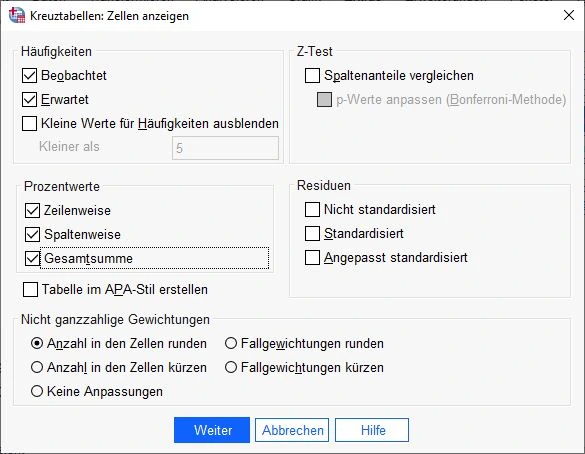
In dem Dialogfenster wählen wir folgende Optionen:
– Beobachtet
– Erwartet
– Zeilenweise
– Spaltenweise
– GesamtsummeChi-Quadrat Test in SPSS starten

Unsere Einstellungen sind fertig. Wir klicken auf OK und starten die Berechnung.
Analyse Chi-Quadrat Test in SPSS
Nachdem der Chi-Quadrat-Test in SPSS durchgeführt wurde, ist es wichtig, das Ergebnis richtig zu interpretieren, um unsere Studienfrage zu beantworten. In diesem Artikel werden wir uns anschauen, wie man das Ergebnis eines Chi-Quadrat-Tests interpretiert und welche Schlussfolgerungen man daraus ziehen kann. Deshalb blicken wir in die Ausgabe von SPSS und schauen uns die Tabellen und Diagramme an:
Übersicht
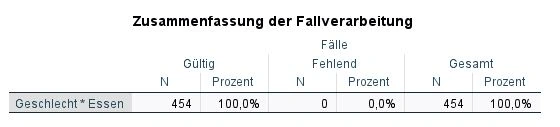
Zunächst schauen wir uns die Tabelle Zusammenfassung der Fallverarbeitung an. Die Zahl N gibt uns die Anzahl der Fälle (engl. Cases) an. In unserem Datensatz haben N=454 Personen an der Befragung teilgenommen. Alle Fälle konnten verarbeitet werden.
Balkendiagramm: Chi-Quadrat Test in SPSS
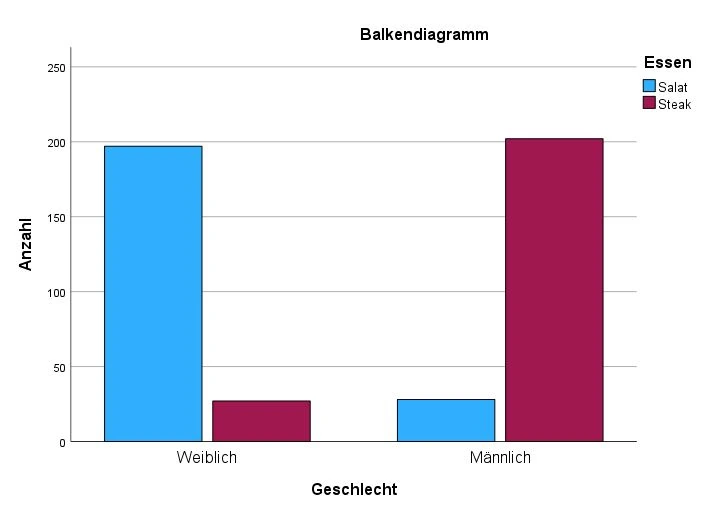
Weiter unten befindet sich das Balkendiagramm. Es zeigt uns eine visuelle Übersicht der Antworten. Wir sehen, dass Frauen deutlich mehr Salat bestellt haben als Steaks, weil der blaue Balken (Salat) deutlich größer als der rote Balken (Steaks) ist. Bei Männern ist es genau umgekehrt. Eine deutliche Mehrheit wählt eher Steaks. In den nächsten Tabellen schauen wir uns die Daten genauer an. Jetzt wissen wir zumindest, dass in welche Richtung die Ergebnisse gehen werden.
Erwartete Anzahl prüfen
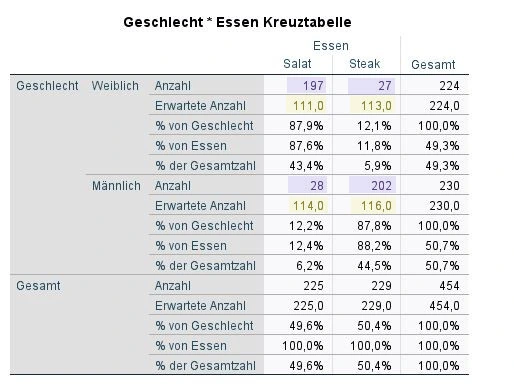
Wir blicken auf die Kreuztabelle für beide Variablen (Geschlecht * Essen). Um die Voraussetzungen für einen gültigen Chi-Quadrattest zu überprüfen, betrachten wir die Zeilen Erwartete Anzahl für Salat und Steak und männlich und weiblich. In unserem Beispiel sind sie gelb markiert. Wir sehen vier Werte und keiner der Werte darf weniger als 5 Fälle klein sein. In unserem Beispiel sehen wir 111, 113, 114 und 116. Alle vier Werte sind jeweils größer als 4. Das ist gut und deshalb können wir mit der Analyse fortfahren.
Die gelb markierten Felder zeigen die erwartete Anzahl und die lila Felder zeigen die beobachteten Felder an. Damit der Chi-Quadrat-Test ein unsere Hypothese bestätigt, müssen die beobachteten Fälle (lila) jeweils deutlich größer bzw. kleiner als die erwartete Anzahl (gelb) sein.
- Frauen essen mit n=197 deutlich mehr Salat als erwartet wurde (n=111). Gleichzeitig essen sie deutlich weniger Steaks (n=27) als erwartet wurde (n=113).
- Männer essen deutlich weniger Salat (n=28) als erwartet wurde (n=114), während andere männliche Versuchsteilnehmer deutlich mehr Steaks (n=202) bestellt haben, als unser Chi-Quadrat Test erwartete (n=116).
Qui-Quadrat-Test Tabelle
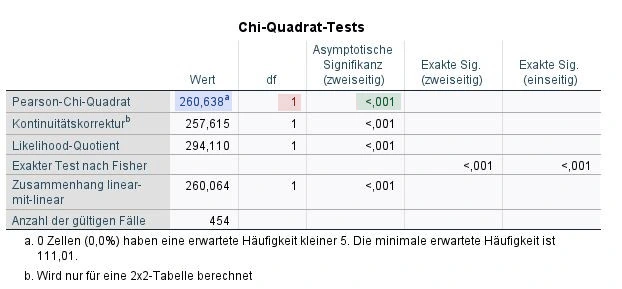
Die Tabelle Chi-Quadrat-Tests ist das Herzstück unserer Analyse. Zunächst blicken wir auf die Fußzeile unter a). Dort sehen wir, wie viele Fälle eine erwartete Häufigkeit kleiner als 5 aufweisen. Das haben wir bereits im letzten Schritt analysiert und hier nochmal bestätigt. 0 Zellen haben sind kleiner als 5, was positiv für unsere Analyse ist und wir deshalb nicht den exakten Test nach Fischer benötigen.
Wir wählen die Werte der Zeile: Pearson-Chi-Quadrat. Sie sind die Basis für unsere finale Gleichung für die Publikation. Bevor wir unsere Gleichung aufstellen können, schauen wir schnell auf die Effektstärke in der Tabelle Symmetrische Maße.
Effektstärke berechnen
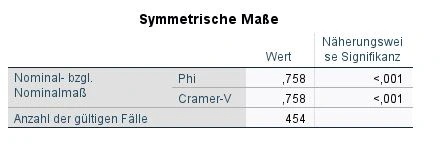
Die Effektstärke gibt uns an, wie stark der Zusammenhang ist, den wir getestet haben. Es gilt: je höher die Effektstärke, desto deutlicher ist der Zusammenhang. Im Grunde verwenden wir in der Regel den Cramer-V Wert. In unserem Beispiel ist V=0.758 und demnach ein sehr großer Effekt.
| φ, V Wert | Interpretation |
|---|---|
| 0.1 | Kleiner Effekt |
| 0.3 | Mittlerer Effekt |
| 0.5 | Großer Effekt |
Finale Gleichung erstellen
Damit wir unsere Berechnungen abschließen können, schreiben wir die Ergebnisse als finale Gleichung auf. Das ist etwas umständlich, weil wir uns die Ergebnisse aus zwei Tabellen zusammensuchen müssen.
χ²(1) = 260.64, p < .001, V = 0.26Was bedeuten diese Zahlen?
- χ² ist die Bezeichnung für den Chi-Quadrat Test für Unabhängigkeit.
- (1) Sind die Freiheitsgrade (in der Tabelle als df bezeichnet)
- Dieser Wert wird in der Teststatistik nachgeschlagen, um den p WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. zu berechnen.
- p: Das ist der Signifikanzwert. Einem Signifikanzniveausignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist. von α=0.05 sollte der p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. unter dem Signifikanzniveau liegen.
- V = ist die Effektstärke
Fazit
Wenn das Ergebnis des Chi-Quadrat-Tests signifikant ist, gibt es einen Zusammenhang zwischen den Variablen, während ein nicht signifikantes Ergebnis darauf hindeutet, dass kein Zusammenhang besteht. Insgesamt ist der Chi-Quadrat-Test eine nützliche Methode, um die Beziehungen zwischen kategorialen Variablen zu untersuchen und zu verstehen.
In unserem Beispiel konnten deutlich aufzeigen, dass laut der untersuchten Studie Männer mehr Steaks und Frauen mehr Salat essen.
4 Fakten über Chi-Quadrat Test für Unabhängigkeit
- Der Chi-Quadrat-Test ist ein wichtiges statistisches Verfahren, das verwendet wird, um zu überprüfen, ob es einen Zusammenhang zwischen zwei kategorialen Variablen gibt.
- Der Chi-Quadrat-Test wird häufig in der Sozialwissenschaft, Psychologie und anderen Bereichen verwendet, in denen man sich für die Beziehungen zwischen verschiedenen Merkmalen interessiert.
- Um die Chi-Quadrat-Statistik zu berechnen, werden die Unterschiede zwischen den tatsächlichen und den erwarteten Häufigkeiten für jede Kategorie quadriert und dann durch die erwarteten Häufigkeiten geteilt.
- Je größer die Chi-Quadrat-Statistik ist, desto größer ist der Unterschied zwischen den tatsächlichen und den erwarteten Häufigkeiten und desto wahrscheinlicher ist es, dass es einen signifikanten Unterschied zwischen den Variablen gibt.
Häufig gestellte Fragen und Antworten: Qui-Quadrat Test SPSS
Was sagt der Chi Quadrat Test aus?
Der Chi-Quadrat-Test in SPSS ist ein nützliches Werkzeug, um zu überprüfen, ob es einen Zusammenhang zwischen zwei kategorialen Variablen gibt. Nachdem der Test durchgeführt wurde, kann man das Ergebnis interpretieren, um festzustellen, ob es einen signifikanten Unterschied zwischen den Variablen gibt oder nicht.
Wann mache ich einen Chi Quadrat Test?
Ein Chi-Quadrat-Test wird verwendet, um zu überprüfen, ob es einen Zusammenhang zwischen zwei kategorialen Variablen gibt. Eine kategoriale Variable ist eine Variable, die in Kategorien eingeteilt ist, die keine Rangfolge haben, wie zum Beispiel Geschlecht, Alter oder Bildungsniveau. Wenn Sie vermuten, dass es einen Zusammenhang zwischen zwei kategorialen Variablen gibt, könnte es sinnvoll sein, einen Chi-Quadrat-Test durchzuführen, um diese Hypothese zu überprüfen.
Es gibt jedoch einige Voraussetzungen, die erfüllt sein müssen, damit ein Chi-Quadrat-Test durchgeführt werden kann. Eine dieser Voraussetzungen ist, dass die Daten in einem Kreuztabellenformat vorliegen müssen, in dem jede Zeile eine kategoriale Variable darstellt und jede Spalte eine andere kategoriale Variable. Außerdem müssen die Messungen unabhängig sein, was bedeutet, dass der Wert einer Messung nicht von den Werten in einer anderen Gruppe abhängen oder von ihnen beeinflusst werden darf. Wenn diese Voraussetzungen erfüllt sind, können Sie einen Chi-Quadrat-Test durchführen, um zu überprüfen, ob es einen Zusammenhang zwischen den kategorialen Variablen gibt.
Was bedeutet Signifikanz 2-seitig?
Signifikanz 2-seitig bedeutet, dass bei der Berechnung der Signifikanz eines Tests beide Seiten der möglichen Ergebnisse berücksichtigt werden. Im Allgemeinen gibt es zwei mögliche Ergebnisse für einen Test: entweder wird die Nullhypothese verworfen oder sie wird nicht verworfen. Die Nullhypothese ist die Annahme, dass es keinen Unterschied zwischen den untersuchten Variablen gibt. Wenn bei einem Test die Nullhypothese verworfen wird, bedeutet dies, dass es einen signifikanten Unterschied zwischen den Variablen gibt.
Bei einem 2-seitigen Signifikanztest werden sowohl die Möglichkeit, dass die Nullhypothese verworfen wird, als auch die Möglichkeit, dass sie nicht verworfen wird, berücksichtigt. Dies bedeutet, dass es zwei mögliche Ergebn
Wann ist Chi-Quadrat signifikant SPSS?
Ein Chi-Quadrat-Test ist signifikant, wenn es einen signifikanten Unterschied zwischen den kategorialen Variablen gibt, die untersucht werden. In SPSS wird die Signifikanz des Chi-Quadrat-Tests mithilfe des p-Werts berechnet. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das tatsächliche Ergebnis des Tests durch Zufall zustande gekommen ist, wenn die Nullhypothese tatsächlich wahr ist.
Wenn der p-Wert kleiner ist als der festgelegte Signifikanzniveau (häufig 0,05 oder 0,01), bedeutet dies, dass das Ergebnis des Tests signifikant ist und es einen signifikanten Unterschied zwischen den Variablen gibt. Wenn der p-Wert jedoch größer ist als das Signifikanzniveau, bedeutet dies, dass das Ergebnis des Tests nicht signifikant ist und es keinen signifikanten Unterschied zwischen den Variablen gibt.
Es ist wichtig zu beachten, dass der p-Wert allein nicht das einzige Kriterium ist, das bei der Interpretation des Chi-Quadrat-Tests berücksichtigt. Deshalb verwenden wir die Effektstärke.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn