Die Spearman-KorrelationKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird., auch Rangkorrelation genannt, ist eine statistische Methode zur Messung der Stärke und Richtung einer monotonen Beziehung zwischen zwei Variablen. Im Gegensatz zur Pearson-Korrelation, die die lineare Beziehung zwischen Variablen misst, untersucht die Spearman-Korrelation die monotone Beziehung, die auch als nichtlinear beschrieben werden kann. Es wird häufig in Sozialwissenschaften, Biologie und anderen Bereichen eingesetzt, in denen die Daten nicht unbedingt normalverteilt sind.
Was berechnet die Spearman Korrelation?
Die Spearman-Korrelation berechnet die Stärke und Richtung einer monotonen Beziehung zwischen zwei Variablen. Dies bedeutet, dass sie die Ähnlichkeit zwischen den Rangreihen beider Variablen misst, anstatt die Ähnlichkeit zwischen den tatsächlichen Werten. Ein Ergebnis von 1 zeigt eine perfekte positive Korrelation an, wobei die Rangreihen beider Variablen identisch sind. Ein Ergebnis von -1 zeigt eine perfekte negative Korrelation an, bei der die Rangreihen beider Variablen genau entgegengesetzt sind. Ein Ergebnis von 0 zeigt keine Korrelation an.
Es ist wichtig zu beachten, dass die Spearman-Korrelation nur die lineare Beziehung zwischen Variablen misst und nicht die KausalitätKausalität Kausalität bezieht sich auf den Zusammenhang zwischen zwei oder mehr Ereignissen oder Variablen, bei dem ein Ereignis oder eine Variable (die Ursache) das andere Ereignis oder die andere Variable (die Wirkung) verursacht..
Der Unterschied zwischen Kausalität und Korrelation
Der Spearman-Korrelationskoeffizient misst lediglich die Stärke und Richtung einer monotonen Beziehung zwischen zwei Variablen. Es sagt nichts darüber aus, ob eine Variable die andere beeinflusst (Kausalität). Es gibt Fälle, in denen eine starke Korrelation zwischen zwei Variablen besteht, aber keine Kausalität vorliegt. Dies wird oft durch gemeinsame Dritteffekte verursacht, das heißt, dass eine dritte Variable die beiden anderen beeinflusst, was zu einer Korrelation zwischen ihnen führt. Es ist auch möglich, dass eine Korrelation aufgrund von Zufall oder Messfehler entsteht. Um Kausalität zu belegen, sind weitere Studien erforderlich, wie zum Beispiel experimentelle oder kausal-analytische Methoden.
Wann wird die Spearman-Rho Korrelation verwendet?
Die Spearman-Korrelation wird in vielen Bereichen verwendet, insbesondere in den Sozialwissenschaften, Biologie, Medizin und anderen Bereichen, in denen die Daten nicht unbedingt normalverteilt sind. Es wird häufig verwendet, wenn die Daten ordinal, interval oder Ratio sind. Einige Beispiele für die Verwendung der Spearman-Korrelation sind:
- In der Medizin, um die Beziehung zwischen bestimmten Risikofaktoren und einer Krankheit zu untersuchen.
- In der Biologie, um die Beziehung zwischen zwei biologischen Variablen, wie zum Beispiel Größe und Gewicht von Tieren, zu untersuchen.
- In den Sozialwissenschaften, um die Beziehung zwischen verschiedenen Variablen wie Bildungsniveau und Einkommen zu untersuchen.
- In der Psychologie, um die Beziehung zwischen verschiedenen psychologischen Variablen wie Persönlichkeit und Lebenszufriedenheit zu untersuchen.
Es ist wichtig zu beachten, dass die Spearman-Korrelation nicht geeignet ist, wenn die Daten nominal sind. In diesem Fall kann die Kappa-Korrelation oder die Chi-Quadrat-Independenztest verwendet werden.
Vorrausetzung
Der Spearman-Rangkorelationskoeffizient ist deutlich robuster als die Berechnungen mit dem Pearson Korrelationskoeffizienten, wenn es um AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind., NormalverteilungNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. oder die SkalenniveausSkalenniveau Das Skalenniveau bezieht sich auf den Typ von Daten, der in einer Studie erhoben wurde, und gibt an, wie die Daten in Bezug auf die Messbarkeit und die Möglichkeit zur Verwendung von Statistiken kodifiziert sind. geht. Hier sind die Bedingungen:
- Beide Variablen müssen mindestens ordinalskaliert sein.
- Falls beide Variablen intervallskaliert sind, sollte die Pearson-Produkt-Moment Korrelation verwendet werden.
- Nominal skalierte Variablen sollten nicht verwendet werden.
- Mehr über Skalenniveaus herausfinden.
Spearman Korrelation in SPSS berechnen
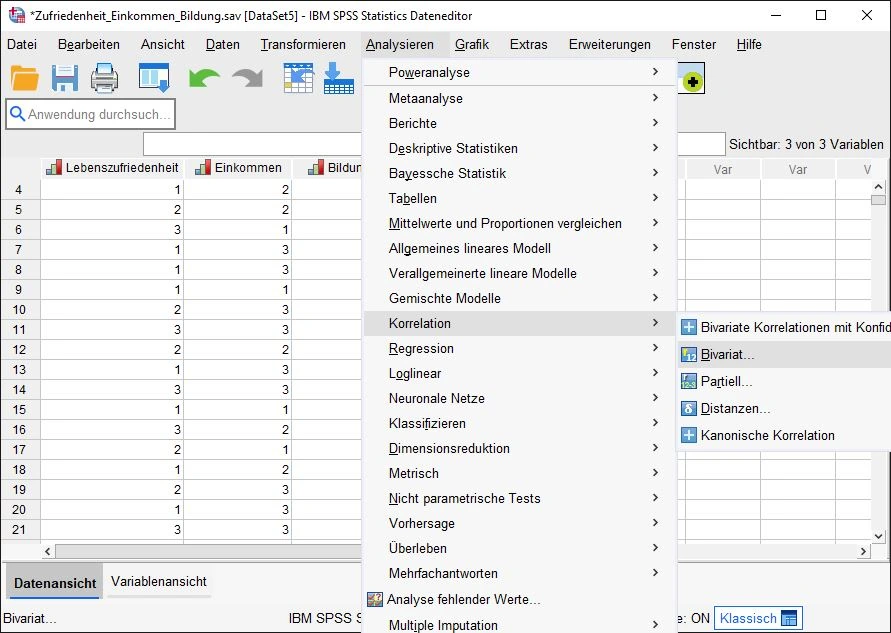
Auswahl im Menü

Im Menü klicken wir oben auf Analysieren > Korrelation > Bivariat
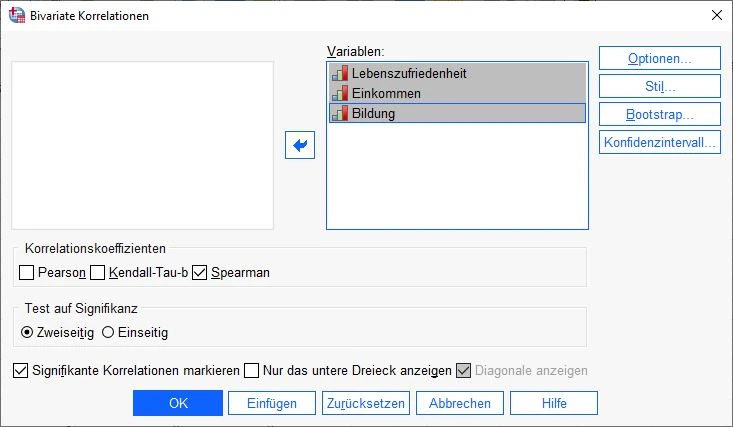
Variablen zuordnen

Es erscheint ein Dialogfenster. Im linken Feld befinden sich alle verfügbaren Variablen aus unserem Datensatz. Auf der rechten Seite befindet sich ein Feld mit der Überschrift Variablen. Wir ziehen alle Variablen hier hin, die wir überprüfen möchten.
Unter den Feldern haben wir mehrere Optionen zur Berechnung von KorrelationenKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird.. Wir setzen einen Haken bei Spearman.
Der Test auf Signifikanz ist in der Regel zweiseitig.
Wir setzen einen Haken bei signifikante Korrelationen markieren. Bei großen Tabellen mit vielen Variablen ist das sehr hilfreich.
In unserem Beispiel sind das die Variablen Lebenszufriedenheit, Einkommen, Bildung.
Anschließend klicken wir auf der rechten Seite den Optionen-Knopf.
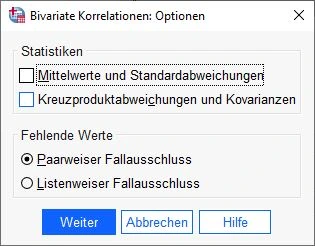
Optionen auswählen

Es erscheint das Optionen-Fenster für Bivariate Korrelationen. Hier stellen wir sicher, dass keine Statistik ausgewählt ist (weil wir sie nicht brauchen).
Darüber hinaus sollte bei Fehlenden Werte die Option „Paarweiser Fallauschluss“ ausgewählt werden.
Wir bestätigen unsere Eingaben mit einem Klick auf den Weiter-Knopf.
Bereit zu starten

Wir sind bereit und klicken auf OK. Die Berechnungen starten. Die Ergebnisse sehen wir in der Ausgabe Datei von SPSS.
Spearman-Rho Korrelation in SPSS analysieren
Den Korrelationskoeffizienten nach Spearman bestimmten
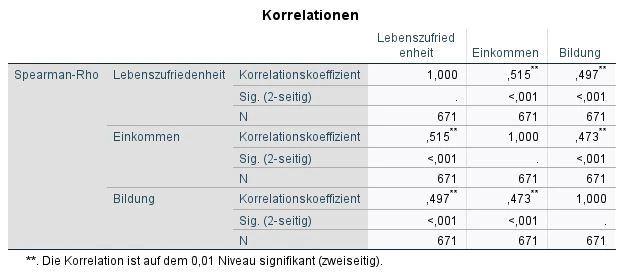
In der Ausgabedatei von SPSS erscheint eine Tabelle mit dem Namen Korrelationen. Diese Tabelle stellt unsere Variablen gegenüber. Aus diesem Grund spiegeln sich die Ergebnisse.
Wir schauen auf die erste Zeile und den Wert der Spearman-Rho-Korrelation. Wir sehen, dass der Korrelationskoeffizient für Lebenszufriedenheit gegenüber Einkommen (r=.515) und Lebenszufriedenheit gegenüber Bildung (r=.497). Darüber hinaus korreliert Einkommen mit Bildung mit r=.473.
Als zweites schauen wir uns die Signifikanz an, um zu überprüfen, ob die Ergebnisse zufällig waren oder nicht. Deshalb schauen wir auf die Zeile Signifikanz (Sig.). Sie gibt uns den p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. an. In unserem Beispiel sehen wir eine Signifikanz von p <.001. Das Ergebnis gleichen wir mit dem Signifikanzniveausignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist. ab.
N beschreibt die Stichprobengröße, die für die Rechnung verwendet wurde. In unserem Beispiel wurden keine Fälle ausgeschlossen.
Was ist das Signifikanzniveau und der p-Wert?
Das Signifikanzniveau in der Statistik gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis zufällig auftritt, wenn es tatsächlich keine Wirkung gibt. Es wird in der Regel als Alpha-Wert (α) angegeben und ist in der Regel auf 0,05 oder 0,01 festgelegt. Der Alpha-Wert gibt die Wahrscheinlichkeit an, dass ein Fehler des Typs I (falsch positive Entscheidung) gemacht wird, wenn tatsächlich keine Wirkung vorliegt.
Der p-Wert ist ein statistischer Maßstab, der die Wahrscheinlichkeit angibt, dass ein bestimmtes Ergebnis oder eine größere Abweichung von Null zufällig auftritt. Wenn der p-Wert kleiner ist als das vorab festgelegte Signifikanzniveau (α), wird das Ergebnis als signifikant angesehen. Das bedeutet, dass es unwahrscheinlich ist, dass das Ergebnis zufällig auftritt und es wahrscheinlich einen wirklichen Effekt gibt. Wenn der p-Wert größer ist als das Signifikanzniveau, wird das Ergebnis als nicht signifikant angesehen und es wird keine Wirkung vermutet.
Signifikanzen können weder 0 noch 1 sein, sondern immer dazwischen liegen. In diesem Fall würden wir den Wert als p<.001
Was sind positive und negative Korrelationen?
Der Unterschied zwischen einer positiven und negativen Korrelation besteht darin, wie die Werte der beiden Variablen zusammen variieren.
Eine positive Korrelation bedeutet, dass die Werte der beiden Variablen tendenziell in die gleiche Richtung abweichen. Wenn eine Variable ansteigt, steigt die andere Variable tendenziell auch an und umgekehrt. Ein Beispiel dafür wäre die Korrelation zwischen Alter und Erfahrung in einem Beruf, je älter man wird, desto mehr Erfahrung hat man in einem Beruf.
Eine negative Korrelation bedeutet, dass die Werte der beiden Variablen tendenziell in entgegengesetzte Richtungen abweichen. Wenn eine Variable ansteigt, fällt die andere Variable tendenziell und umgekehrt. Ein Beispiel dafür wäre die Korrelation zwischen Alter und Körpertemperatur, je älter Menschen werden, desto geringer ist die Körpertemperatur.
Ergebnisse interpretieren
Der Korrelationskoeffizient nach Spearman ist einfach zu interpretieren. Hierfür schauen wir auf diese Tabelle nach Cohen (1988)
| Wert des Korrelationskoeffizienten | Interpretation |
|---|---|
| |r| = .10 | schwach (gering) |
| |r| = .30 | moderat (mittlere) |
| |r| = .50 | stark (groß) |
Ergebnisse publizieren
Die Berechnungen mit des Spearman Korrelationskoeffizienten zeigen eine starke Korrelation zwischen den Variablen Lebenszufriedenheit und Einkommen, r=.515, p<.001; Lebenszufriedenheit und Bildung, r=.497,p<.001 und Einkommen und Bildung, r=.473, p<.001.
5 Fakten zur Spearman-Rho Korrelation
- Die Spearman-Korrelation misst die Stärke und Richtung einer monotonen Beziehung zwischen zwei Variablen.
- Es untersucht die Ähnlichkeit zwischen den Rangreihen beider Variablen, anstatt die Ähnlichkeit zwischen den tatsächlichen Werten.
- Der Spearman-Korrelationskoeffizient liegt immer zwischen -1 und 1, wobei 1 eine perfekte positive Korrelation und -1 eine perfekte negative Korrelation darstellt.
- Es ist nicht notwendig, dass die Daten normalverteilt sind, um die Spearman-Korrelation zu berechnen.
- Es ist eine nichtparametrische Methode, das heißt, es erfordert keine Annahmen über die Verteilung der Daten, im Gegensatz zur Pearson Korrelation, die normalverteilte Daten voraussetzt
Häufig gestellte Fragen und Antworten: Spearman-Rho Korrelation
Was sagt die Spearman Korrelation aus?
Die Spearman-Korrelation gibt Auskunft über die Stärke und Richtung einer monotonen Beziehung zwischen zwei Variablen. Ein Ergebnis von 1 zeigt eine perfekte positive Korrelation an, das heißt, dass die Rangreihen beider Variablen identisch sind. Ein Ergebnis von -1 zeigt eine perfekte negative Korrelation an, das heißt, dass die Rangreihen beider Variablen genau entgegengesetzt sind. Ein Ergebnis von 0 zeigt keine Korrelation an. Es ist wichtig zu beachten, dass die Spearman-Korrelation nur die Stärke und Richtung einer monotonen Beziehung zwischen zwei Variablen misst und nicht die Kausalität beschreibt. Eine starke Korrelation zwischen zwei Variablen bedeutet nicht, dass eine Variable die andere beeinflusst.
Wann ist eine Spearman Korrelation signifikant?
Eine Spearman-Korrelation ist signifikant, wenn der p-Wert des Korrelationskoeffizienten unter einem bestimmten Signifikanzniveau liegt. Der p-Wert gibt an, wie wahrscheinlich es ist, dass ein bestimmter Korrelationskoeffizient zufällig aufgrund von Zufall oder Messfehlern entsteht. In der Regel wird ein Signifikanzniveau von 0,05 verwendet, das bedeutet, dass ein p-Wert unter 0,05 als signifikant angesehen wird. Wenn der p-Wert unter 0,05 liegt, kann man schlussfolgern, dass es eine signifikante Korrelation zwischen den Variablen gibt und es ist unwahrscheinlich, dass die Korrelation durch Zufall entsteht. Es gibt jedoch auch andere Signifikanzniveaussignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist., wie 0.01 oder 0.1, die je nach Kontext und Anforderungen verwendet werden können.
Wann wird die Korrelation nach Spearman-Rho verwendet?
Die Korrelation nach Spearman-Rho wird verwendet, wenn die Daten nicht unbedingt normalverteilt sind. Es eignet sich insbesondere für ordinale, Interval oder Ratio-Daten. Einige Beispiele für die Verwendung der Spearman-Korrelation sind:
– In der Medizin, um die Beziehung zwischen bestimmten Risikofaktoren und einer Krankheit zu untersuchen.
– In der Biologie, um die Beziehung zwischen zwei biologischen Variablen, wie zum Beispiel Größe und Gewicht von Tieren, zu untersuchen.
– In den Sozialwissenschaften, um die Beziehung zwischen verschiedenen Variablen wie Bildungsniveau und Einkommen zu untersuchen.
– In der Psychologie, um die Beziehung zwischen verschiedenen psychologischen Variablen wie Persönlichkeit und Lebenszufriedenheit zu untersuchen.
– In der Finanzwissenschaft, um die Beziehung zwischen verschiedenen Finanzvariablen wie Aktienkurse und Unternehmensgewinne zu untersuchen.
– In der Umweltwissenschaft, um die Beziehung zwischen verschiedenen Umweltvariablen wie Luftqualität und Gesundheit zu untersuchen.
Es ist auch wichtig zu beachten, dass die Spearman-Korrelation nicht geeignet ist, wenn die Daten nominal sind. In diesem Fall kann die Kappa-Korrelation oder die Chi-Quadrat-Independenztest verwendet werden.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn