Was ist die einfache lineare Regression?
Die lineare Regression beschreibt die Art der linearen Beziehung zwischen zwei Variablen. Wie hängt die Schuhgröße mit der Körpergröße zusammen? Um wie viel sinkt der Preis eines Gebrauchtwagens mit jedem gefahrenen Kilometer?
In diesem Tutorial lernst du, eine einfache lineare Regression mit SPSS durchzuführen und zu interpretieren. Verwende dazu deine eigenen Daten oder unsere Beispieldaten.
In unserem Beispiel erstellen wir ein statistisches Modell, das uns hilft, den Wert eines Gebrauchtwagens in Abhängigkeit von einer Variablen (Prädiktor) zu bestimmen. Konkret untersuchen wir den Zusammenhang zwischen dem Kilometerstand eines Autos und seinem Preis auf dem Gebrauchtwagenmarkt. Gibt es einen Zusammenhang und wenn ja, wie hoch ist der Wertverlust pro gefahrenem Kilometer? Am Ende dieses Leitfadens erhalten wir eine präzise Antwort.
Wie funktioniert die lineare Regression?
Um das Konzept der linearen Regression zu verstehen, betrachten wir zunächst die Verteilung der Daten. In unserem Beispiel vergleichen wir die Variablen Preis und Kilometerstand. In unserem Beispiel befinden sich N=249 Fahrzeuge mit den Werten Preis und Kilometerstand im Datensatz. Jeder Datenpunkt repräsentiert einen Fall, in unserem Fall ein Auto. Das folgende Diagramm zeigt die Verteilung der Fahrzeuge.
Das Ziel der Analysen in diesem Handbuch ist die Erstellung einer Regressionsgleichung. Mit anderen Worten, wir suchen nach einer Geraden, die den Zusammenhang in den Daten möglichst gut beschreibt. Sinkt im Allgemeinen der Preis pro gefahrenen Kilometer und wenn ja, um wie viel? Als Ergebnis erhalten wir eine Regressionsgleichung, die wie folgt aussieht:

Keine Angst, wir brauchen noch keine großen mathematischen Kenntnisse. Nur so viel: y ist die Zielvariable. Da wir eine Gleichung aufstellen wollen, die den Preis in Abhängigkeit von den gefahrenen Kilometern bestimmt, ist die Zielvariable (y) der Preis. Die Variable b1 ist die Prädiktorvariable (Fahrleistung). In unserem Diagramm könnte die rote Gerade den Zusammenhang beschreiben. Möglicherweise beschreibt die grüne Gerade einen stärkeren Zusammenhang. Mit dieser Anleitung berechnen wir Schritt für Schritt die perfekte Gerade für unsere Daten.

Voraussetzungen prüfen
- LinearitätLinearität Linearität bezieht sich auf die Beziehung zwischen zwei oder mehr Variablen, die durch eine gerade Linie dargestellt wird, bei der die Veränderung einer Variablen direkt proportional zur Veränderung der anderen Variable ist. prüfen: Linearität sollte bei beiden Variablen gegeben sein. Eine Anleitung zur Prüfung der Linearität.
- AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind. prüfen: Ausreißer sind Werte, die im ungewöhnlich klein oder groß sind und einen negativen Einfluss auf die Analyse haben, weil sie die Ergebnisse verfälschen. Je weniger Ausreißer ein Datensatz hat, desto besser. Anleitung zur Prüfung der statistischen Ausreißer.
- Multikollinearität prüfen: Wenn zwei Variablen eine sehr starke positive oder negative KorrelationKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird. (|r|>.90) haben spricht man in der Statistik von Multikollinearität. Hier gleichen sich die Variablen zu sehr und beinhalten zu ähnliche Informationen, was sich negativ bei der Interpretation der Ergebnisse auswirkt. Die zu untersuchenden Variablen dürfen keine Multikollinearität aufweisen. Anleitung zur Überprüfung der Korrelation.
- Weitere Voraussetzungen prüfen: Um eine gültige lineare Regression zu berechnen, sollten noch weitere Kennzahlen analysiert werden (wie Homoskedastizität der ResiduenResiduen Residuen sind die Abweichungen zwischen den beobachteten Daten und den durch ein statistisches Modell vorhergesagten Daten und werden verwendet, um die Anpassung des Modells an die Daten zu beurteilen und um mögliche Muster oder Trends in den Daten zu erkennen. Sie können auch verwendet werden, um die Validität und Zuverlässigkeit von Vorhersagemodellen zu überprüfen., Normalverteilung der Residuen und Unabhängigkeit der Residuen). Diese stehen erst nach der Berechnung der Regression zur Verfügung und werden dementsprechend bei der Interpretation der Ergebnisse besprochen.
Berechnung der einfachen linearen Regression in SPSS
Berechnung der einfachen linearen Regression in SPSS
Auswahl Menü

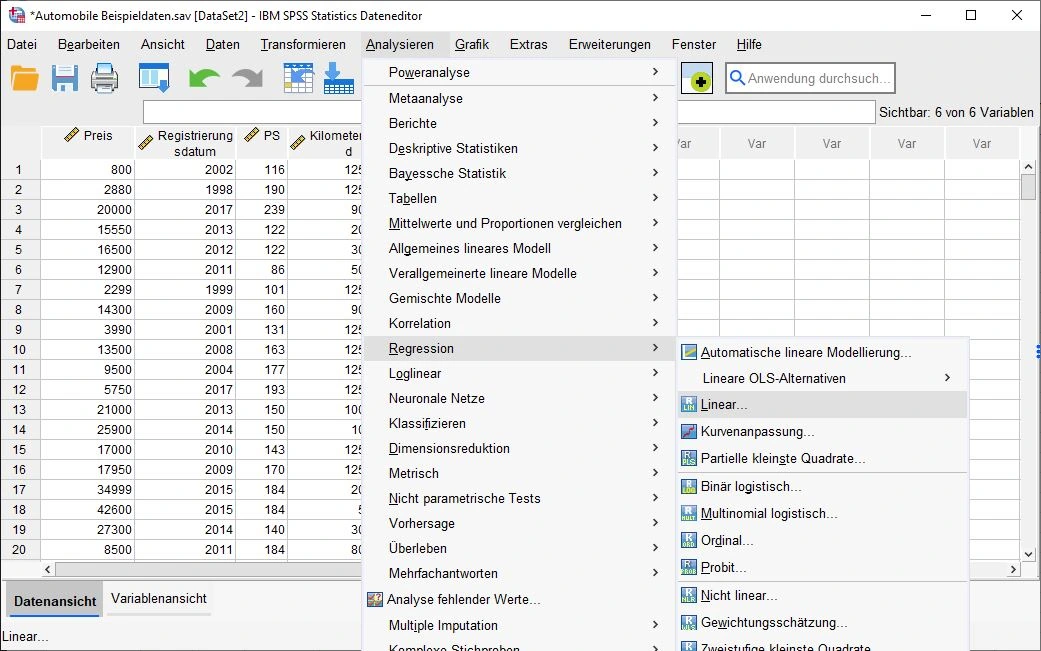
Los geht es. Wir navigieren zu Analysieren > Regression > Linear… .
Dialogfenster Lineare Regression

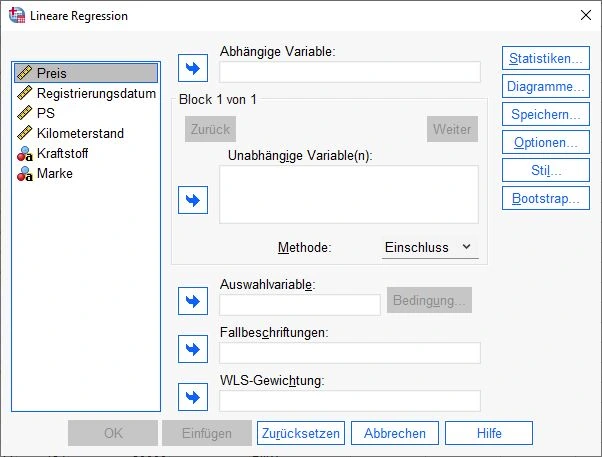
Es erscheint das Dialogfenster „Lineare Regression“. An dieser Stelle ziehen wir die Zielvariable auf das Feld Abhängige Variableabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. . Die Prädiktorvariable kommt in das Feld unabhängige Variable(n).
Auswahl der Variablen

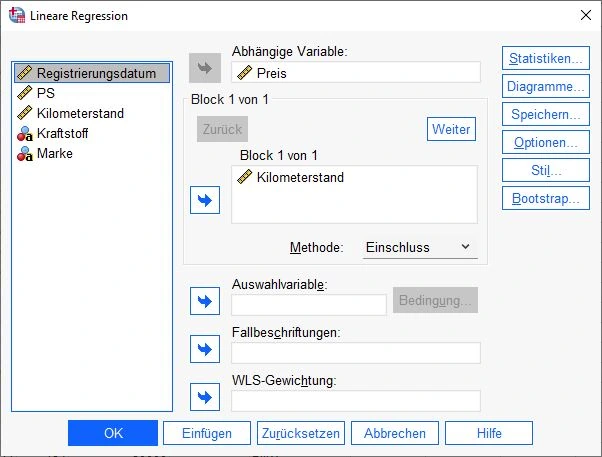
In unserem Beispiel sieht das so aus: Die Variable Preis befindet sich im Feld Abhängige Variable und Kilometerstand im Feld unabhängige Variable.
Anschließend klicken wir in diesem Dialogfenster auf den Knopf Statistiken.
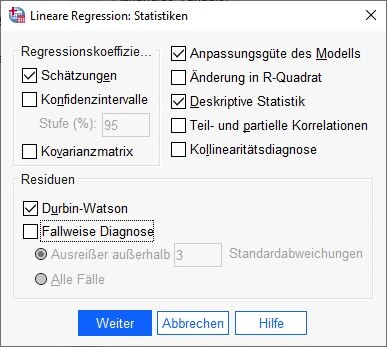
Statistiken einstellen

Im geöffneten Statistik-Dialogfenster nehmen wir die ersten Einstellungen vor. Im Feld Regressionskoeffizienten setzen wir ein Häkchen bei Schätzer. Außerdem müssen die Optionen Anpassungsgüte des Modells, Deskriptive Statistik und weiter unten Durbin-Watson im Feld Residuen angekreuzt werden.
Die Eingaben werden mit Weiter bestätigt.
Hinweis: In diesem Dialogfenster können weitere Optionen wie Kollinearitätsdiagnose oder Änderung in R-Quadrat ausgewählt werden. Diese liefern interessante Informationen. Um dieses Tutorial so einfach wie möglich zu halten, werden wir die Komplexität so gering wie möglich halten und nur die absolut notwendigen Kennzahlen betrachten.
Auswahl Diagramme

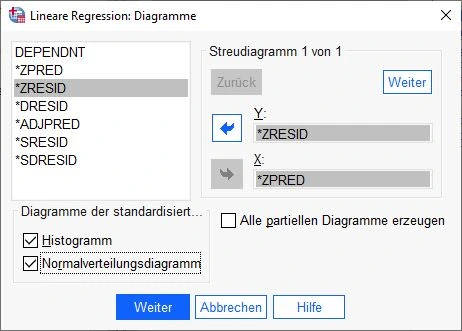
Wenn wir uns wieder im vorigen Fenster befinden, klicken wir nun auf die Schaltfläche „Diagramme„.
Diagramme einstellen

Im Dialogfenster wird ZRESID für das Y-Feld und ZPRED für das X-Feld ausgewählt, wie in der folgenden Abbildung gezeigt. Im Feld Diagramme der standardisierten Residuen müssen die beiden Kontrollkästchen Histogramm und Normalverteilungsdiagramm aktiviert sein.
Klicken Sie auf die untere Schaltfläche „Weiter„, um die Einstellungen zu übernehmen.
Einfache lineare Regression in SPSS starten

Klicken Sie auf OK, um die Berechnung der linearen Regression mit SPSS zu starten.
Ergebnisse Analysieren SPSS einfache linare Regression
Durbin-Watson-Statistik
Die Unabhängigkeit der Residuen prüfen wir in SPSS mit der Durban-Watson-Statistik. Die Tabelle mit den Daten befindet sich in der Ausgabe und heißt „Modellzusammenfassung.

der Wert höher als 2 ist
der Wert niedriger als -2
Wenn wir in der Prüfung einen Wert zwischen 2 und -2 erzielen, können wir davon ausgehen, dass keine Autokorrelation auftritt. Die Durbin-Watson-Statistik kann theoretisch einen Wert von 4 bis -4 annehmen.
In unserem Beispiel sehen wir einen Wert von 1,368. Eine Autokorrelation tritt nach Durbin-Watson-Statistik nicht auf.
Was tun, wenn es eine Autokorrelation gibt?
Falls eine Autokorrelation stattfindet, sollte ein weiteres Verfahren verwendet werden, wie Heteroskedastizität-und-Autokorrelations-konsistente Schätzer (Newey-West-Schätzer oder HAC).
Multikollinearität prüfen mit KorrelationenKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird.
Wenn zwei oder mehr Variablen eine hohe Korrelation aufweisen, weisen sie auf ähnliche Informationen in den Daten hin. Um eine genaue Berechnung der Regressionskoeffizienten zu gewährleisten, sollte das endgültige Modell Prädiktoren verwenden, die nicht zu stark korreliert sind. Eine Möglichkeit, die Multikollinearität zu überprüfen, ist die Analyse der Korrelationen anhand der Korrelationstabelle.
In diesem Leitfaden wird daher auf die Korrelationstabelle (Korellationen) Bezug genommen.
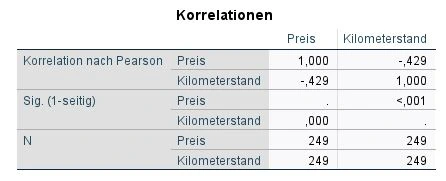
In der Tabelle beziehen wir uns auf die oberen Zeilen, die die Korrelation nach Pearson darstellen, d.h. Preis und Kilometerleistung. Diese Variablen werden in Spalten und Zeilen dargestellt, was einen einfachen Vergleich der Korrelationen zwischen den Variablen ermöglicht.
Die Korrelationswerte reichen von 1 bis -1, wobei eine Korrelation von 1 eine perfekte Übereinstimmung, eine Korrelation von -1 eine perfekte negative Übereinstimmung und eine Korrelation von 0 keine Übereinstimmung bedeutet.
Was ist eine Korrelation?
Wenn zwei Variablen eine Korrelation von 0,7 oder mehr aufweisen, spricht man von Multikollinearität. Dasselbe gilt für negative Werte von -0,7 oder weniger.
In unserem Beispiel betragen die Korrelationen -0,429 usw. Multikollinearität kann somit ausgeschlossen werden.
Lineare Regression Histogramm analysieren
Dieses Histogramm zeigt die Häufigkeit und die Verteilung der Residuen für die Variable Preis.
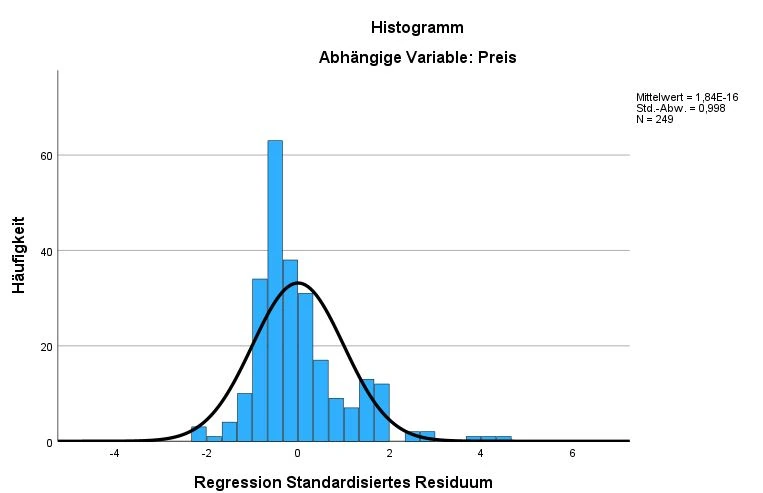
In unserem Beispiel weisen die Residuen für die Variable Preis eine gute Übereinstimmung mit der NormalverteilungNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. auf, was positiv zu bewerten ist. Im oberen rechten Teil des Diagramms sind der Mittelwert, die StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. und die Anzahl der Fälle (N) angegeben. Es ist wünschenswert, dass der Mittelwert bei 0 und die Standardabweichung bei 1 liegt, während die Fallzahl ausreichend hoch sein sollte.
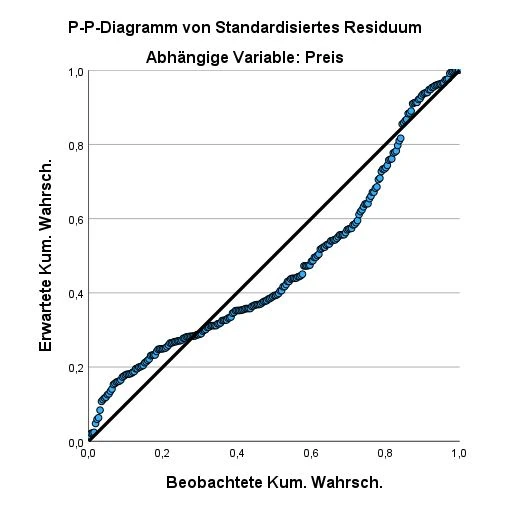
Analyse des PP Plots
Dieses P-P-Plot-Diagramm zeigt, dass die beobachteten Werte (als Kreise dargestellt) gut mit den erwarteten Werten (als Linie dargestellt) übereinstimmen. Es ist nicht perfekt, aber innerhalb eines akzeptablen Bereichs. Je näher die beobachteten Werte an der Linie liegen, desto besser. Wenn sie weit von der Linie entfernt sind, spricht dies gegen eine Normalverteilung.
Methode: Shapiro-Wilk-Test
Die Normalverteilung kann mittels Shapiro-Wilk-Test mit der Variable SRE_1 stattfinden.
Hier gibt es die Anleitung für den Shapiro-Wilk-Test.
Was passiert, wenn die Normalverteilung nicht gegeben ist?
- Du rechnest einfach weiter und ziehst die Ergebnisse heran. In der Regel ist die multiple lineare Regression ziemlich robust gegen eine Verletzung und deine Ergebnisse sind immer noch verwendbar.
- Alternativ kannst du deine Daten auch transformieren. Das Problem bei der Transformation ist, dass es zu einer Verschlechterung kommen kann, was in der Statistik auch problematisch ist.
- Eine andere Möglichkeit ist das BootstrappingBootstrapping Bootstrapping ist eine Methode der Datenanalyse, bei der aus einer bestehenden Stichprobe wiederholt neue Stichproben gezogen werden, um die Unsicherheit von Schätzungen und die Stabilität von Statistiken zu untersuchen. Durch das Bootstrapping wird die Verteilung der Schätzungen simuliert und es können Konfidenzintervalle berechnet werden, die eine Aussage über die Wahrscheinlichkeit machen, dass die wahre Population innerhalb eines bestimmten Bereichs liegt. mit SPSS. Diese Option ist in den Einstellungen der multiplen linearen Regression verfügbar.
- Es können auch andere Regressionsmethoden wie die Constrained Nonlinear Regression (CNLR) verwendet werden. Diese ist wesentlich robuster, aber auch komplexer in der Durchführung.
Signifikanz prüfen mit ANOVA
Wir blicken auf die Tabelle ANOVA und dort auf die Spalte ganz rechts: Signifikanz (Sig.).
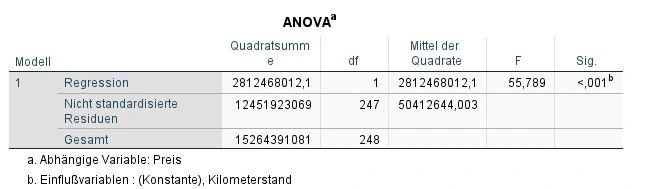
Es wurde untersucht, ob ein signifikanter Zusammenhang zwischen den Variablen besteht oder ob das Ergebnis zufällig ist. In der Statistik wird die Signifikanz durch den p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. ausgedrückt. Je kleiner der p-Wert, desto signifikanter ist das Ergebnis. In einigen Fällen gibt SPSS für sehr kleine p-WerteP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist. p<.001 an, was auf eine hohe Signifikanz hinweist. In unserem Fall ist das Ergebnis hoch signifikant.
Ob das Ergebnis signifikant ist oder nicht, hängt vom verwendeten Signifikanzniveausignifikanzniveau Das Signifikanzniveau, auch als alpha-Niveau bezeichnet, ist der Schwellenwert, der verwendet wird, um zu bestimmen, ob ein Ergebnis in einer Studie statistisch signifikant ist. Es gibt an, wie wahrscheinlich es ist, dass ein bestimmtes Ergebnis oder eine Beobachtung durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. In der Regel wird das Signifikanzniveau auf 0,05 oder 0,01 festgelegt, was bedeutet, dass ein Ergebnis als statistisch signifikant angesehen wird, wenn der p-Wert kleiner als dieser Schwellenwert ist. ab. Es wird mit α bezeichnet und beträgt in der Regel α=.05. Ein Signifikanzniveau von 5% bedeutet, dass wir bereit sind, ein Fehlerrisiko von 5% in Kauf zu nehmen, um das Modellergebnis zu akzeptieren.
Wie hoch sollte das Signifikanzniveau sein?
Der Alpha-Wert dient als Schwellenwert, um zu bestimmen, ob ein Ergebnis auf Zufall oder auf einer tatsächlichen Beziehung zwischen zwei Variablen beruht. In der Regel wird ein Alpha-Wert von 0,05 oder 0,01 verwendet. Ein niedrigerer Alpha-Wert erfordert strengere Bedingungen, um ein Ergebnis als signifikant zu betrachten, während ein höherer Alpha-Wert weniger strenge Bedingungen erfordert. Die Wahl des richtigen Alpha-Wertes hängt von den Zielen der Studie und dem Risiko falscher Ergebnisse ab.
Die Regressionsgleichung
Die Regressionsgleichung ist der Kern unseres Modells. Sie ist die mathematische Formel zur Vorhersage der Werte unserer Zielvariablen.
Was bedeutet die Regressionsgleichung?
In der Regressionsanalyse wird eine Regressionsgleichung verwendet, um die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu beschreiben. Die Regressionsgleichung hat folgende allgemeine Form
In der Regressionsanalyse wird eine Regressionsgleichung verwendet, um die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu beschreiben. Die Regressionsgleichung sieht in der allgemeinen Form wie folgt aus: y = b<sub>0</sub> + b<sub>1</sub> * <mark style="background-color:rgba(0, 0, 0, 0)" class="has-inline-color has-contrast-3-color">x<sub>1</sub></mark> + b<sub>2</sub> * <mark style="background-color:rgba(0, 0, 0, 0)" class="has-inline-color has-contrast-3-color">x<sub>2</sub></mark> + ... + b<sub>n</sub> * <mark style="background-color:rgba(0, 0, 0, 0)" class="has-inline-color has-contrast-3-color">x<sub>n</sub></mark>
In dieser Gleichung ist y die abhängige Variable, die Prädiktorvariable oder die zu erklärende Variable, und x1, x2, …, xn sind die unabhängigen Variablen oder Prädiktoren, die zur Erklärung von y verwendet werden. b0 ist der y-Achsenabschnitt und b1, b2, …, bn sind die Regressionskoeffizienten (auch Steigungskoeffizienten genannt) für die unabhängigen Variablen. Die Regressionskoeffizienten geben an, um wie viel sich y ändert, wenn sich eine unabhängige Variable um 1 ändert, während alle anderen Variablen konstant bleiben.
Die Regressionsgleichung wird verwendet, um y unter Verwendung der bekannten Werte für die unabhängigen Variablen vorherzusagen.
Analyse der Koeffizienten Tabelle
Wir schauen uns die Tabelle Koeffizienten in SPSS an und dort die Spalte „Regressionskoeffizienten B“. In jeder Zeile sehen wir die Werte für unsere abhängigen Variablen: Zulassungsdatum, PS und Kilometerstand sowie die Konstante.
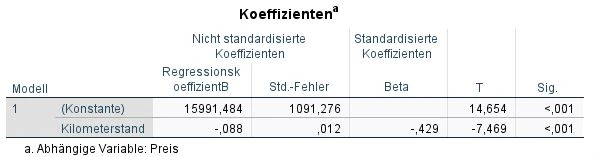
Zum Beispiel, wenn man wissen möchte, wie sich die Anzahl der gefahrenen Kilometer auf den Wert eines Gebrauchtwagens auswirkt. In diesem Fall könnte man eine Regressionsgleichung verwenden, um die Beziehung zwischen diesen beiden Variablen zu beschreiben. Die Regressionsgleichung wird verwendet, um Vorhersagen für den durchschnittlichen Preis bei einem Gebrauchtwagen zu berechnen.
Unsere Gleichung kann sogar mehr: Wenn wir den Kilometerstand eingeben, können wir recht präzise den Preis für einen Gebrauchtwagen bestimmten. Wir müssen lediglich die untere Formel verwenden:
Je niedriger der Kilometerstand, desto höher ist der Preis. Für jeden gefahrenen Kilometer sinkt der Preis um 0,069 EUR
Prüfen der Signifikanzwerte
Im nächsten Schritt prüfen wir die Signifikanz der Koeffizienten. In der Tabelle Koeffizienten blicken wir deshalb auf die Spalte „Sig.“ und sehen die p-Werte.
In unserem Beispiel sind alle Prädiktoren signifikant.
Mein Modell ist signifikant, einzelne Koeffizienten nicht. Was tun?
Das kann an der Multikollinearität liegen, über die wir weiter oben berichtet haben. Ein weiterer Grund sind zu viele Prädiktoren in der Gleichung haben. Wenn es zu viele Prädiktoren oder Fälle (Cases) gibt, kann der Signifikanztest verzerrt werden. In diesem Fall solltest du die nicht signifikante Variable ausschließen und das Modell erneut berechnen.
Effektstärken berechnen
Um die Effektstärken zu berechnen, gibt es einen hervorragenden Rechner auf statistikguru.de
Häufig gestellte Fragen und Antworten: einfache lineare Regression
Wann wende ich eine einfache lineare Regression an?
Die einfache lineare Regression ist ein statistisches Modell zur Beschreibung der Beziehung zwischen einer abhängigen und einer unabhängigen Variablen. Es wird verwendet, um Vorhersagen über die abhängige Variable auf der Grundlage bekannter Werte der unabhängigen Variablen zu machen.
Es gibt mehrere Gründe für die Verwendung der einfachen linearen Regression:
– Einfache Anwendung: Die einfache lineare Regression ist ein einfaches Modell, das leicht zu verstehen und anzuwenden ist. Es erfordert nur geringe statistische Kenntnisse und ist eine gute Wahl, wenn schnelle Vorhersagen benötigt werden.
– Einfache Interpretation: Das einfache lineare Regressionsmodell besteht aus einer Regressionsgeraden, die die Beziehung zwischen den Variablen beschreibt. Dies erleichtert die Interpretation der Ergebnisse und die Schlussfolgerungen über die Beziehung zwischen den Variablen.
– Einfache Vorhersage: Das einfache lineare Regressionsmodell ermöglicht die Vorhersage der abhängigen Variablen auf der Grundlage bekannter Werte der unabhängigen Variablen. Das Modell liefert auch eine Schätzung der Unsicherheit der Vorhersage, die durch den Standardfehler der Schätzungen ausgedrückt wird.
Wann verwenden wir eine einfache und wann eine multiple Regression?
Die einfache Regression wird verwendet, wenn es nur eine unabhängige Variable gibt, die die abhängige Variable erklären soll. Die multiple Regression wird verwendet, wenn mehrere unabhängige Variablen die abhängige Variable erklären sollen.
Eine einfache Regression ist gut geeignet, wenn eine lineare Beziehung zwischen einer abhängigen und einer unabhängigen Variablen untersucht werden soll. Wenn jedoch mehrere Faktoren untersucht werden sollen, die bei der Erklärung der abhängigen Variablen eine Rolle spielen können, ist die multiple Regression die bessere Wahl.
Die multiple Regression ermöglicht es, den Einfluss mehrerer unabhängiger Variablen auf die abhängige Variable zu untersuchen und zu quantifizieren. Sie kann auch verwendet werden, um die relative Bedeutung der einzelnen unabhängigen Variablen zu bestimmen und zu sehen, wie gut sie zusammen die abhängige Variable erklären.
Was ist der Unterschied zwischen Korrelation und Regression?
Der Unterschied zwischen Korrelation und Regression besteht darin, dass die Korrelation die Stärke und Richtung der Beziehung zwischen zwei Variablen misst, während die Regression versucht, die Beziehung zwischen den Variablen zu beschreiben und zu modellieren, um Vorhersagen über eine der Variablen auf der Grundlage bekannter Werte der anderen Variable zu machen.
Die Korrelation wird durch den Korrelationskoeffizienten gemessen, der Werte zwischen -1 und 1 annehmen kann. Ein Wert von -1 bedeutet, dass die Variablen perfekt negativ korreliert sind, d. h. wenn der Wert einer Variablen steigt, sinkt der Wert der anderen Variablen. Ein Wert von 1 bedeutet, dass die Variablen perfekt positiv korreliert sind, d. h. wenn der Wert einer Variablen steigt, steigt auch der Wert der anderen Variablen. Ein Wert von 0 bedeutet, dass keine Korrelation zwischen den Variablen besteht.
Die Regression hingegen versucht, die Beziehung zwischen den Variablen durch eine gerade Regressionsgerade zu modellieren. Die Steigung der Regressionslinie gibt an, wie sich die abhängige Variable ändert, wenn sich die unabhängige Variable ändert, und der y-Achsenabschnitt gibt den Wert der abhängigen Variablen an, wenn die unabhängige Variable 0 ist. Die Regression kann auch verwendet werden, um Vorhersagen über die abhängige Variable auf der Grundlage bekannter Werte der unabhängigen Variable zu machen.
Wann ist eine Regression nichtlinear?
Eine Regression ist nicht linear, wenn die Beziehung zwischen den Variablen, die das Modell beschreibt, nicht durch eine gerade Linie dargestellt werden kann. Stattdessen kann die Beziehung zwischen den Variablen durch eine Kurve oder eine andere Funktion dargestellt werden.
Es gibt verschiedene Anzeichen dafür, dass eine Regression nicht linear ist:
Es gibt mehrere Anzeichen dafür, dass eine Regression nicht linear ist:
– Nicht-lineare Korrelation: Wenn die Korrelation zwischen den Variablen nicht linear ist, könnte dies bedeuten, dass die Regression nicht linear ist. Eine Möglichkeit, die Korrelation zu überprüfen, besteht darin, Korrelationen zu berechnen und die Daten mit Hilfe von Streudiagrammen zu visualisieren.
– Nicht-konstante Varianz: Wenn die Varianz der abhängigen Variable nicht konstant ist, kann dies bedeuten, dass die Regression nicht linear ist. Eine Möglichkeit, die Varianz zu überprüfen, ist die Visualisierung der Residuen mit Hilfe von Histogrammen oder Streudiagrammen.
– Nicht-normale Verteilung der Residuen: Wenn die Residuen der Regression nicht normalverteilt sind, kann dies bedeuten, dass die Regression nicht linear ist. Eine Möglichkeit, die Verteilung der Residuen zu überprüfen, ist die Verwendung von Normalfit-Plots oder Anderson-Darling-Tests.
Es ist wichtig zu beachten, dass diese Anzeichen nicht notwendigerweise bedeuten, dass die Regression nicht linear ist. Sie können auch aus anderen Gründen auftreten. Bei der Entscheidung, ob und wie die Linearität der Regression geprüft werden soll, ist es wichtig, die spezifischen Eigenschaften der Daten und die Fragestellung zu berücksichtigen.
Welche Arten von Regressionen gibt es?
Es gibt verschiedene Arten von Regressionen, die je nach Art der abhängigen und unabhängigen Variablen und der Form der Beziehung zwischen ihnen verwendet werden. Es folgen einige Beispiele für verschiedene Regressionstypen:
– Lineare Regression: Die lineare Regression wird verwendet, um die lineare Beziehung zwischen einer abhängigen und einer unabhängigen Variablen zu beschreiben. Das Modell besteht aus einer Regressionsgeraden, die die Beziehung zwischen den Variablen darstellt.
– Multiple lineare Regression: Die multiple lineare Regression wird verwendet, wenn es mehrere unabhängige Variablen gibt, die die abhängige Variable erklären sollen.
– Polynomielle Regression: Die polynomielle Regression wird verwendet, wenn die Beziehung zwischen den Variablen durch eine Kurve und nicht durch eine Gerade beschrieben werden kann.
– Logistische Regression: Die logistische Regression wird verwendet, wenn die abhängige Variable binär ist, d. h. nur zwei mögliche Werte annehmen kann (z. B. „ja“ oder „nein“). Sie wird häufig verwendet, um die Wahrscheinlichkeit von Ereignissen vorherzusagen.
Es gibt noch weitere Regressionen, wie z.B. die multinominale Regression, auf die hier nicht näher eingegangen werden soll.
Was bedeutet R2 bei Regressionen?
R2 (auch bekannt als „R²“, „Determinationskoeffizient“) ist ein Maß dafür, wie gut ein Regressionsmodell die Variabilität der abhängigen Variablen erklärt. Er wird berechnet, indem der Anteil der Varianz der abhängigen Variablen, der durch das Regressionsmodell erklärt wird, durch die Gesamtvarianz der abhängigen Variablen dividiert wird.
R2 nimmt Werte zwischen 0 und 1 an, wobei ein höherer Wert bedeutet, dass das Regressionsmodell die Variabilität der abhängigen Variablen besser erklärt. Ein R2-Wert von 0 bedeutet, dass das Regressionsmodell keine Erklärung für die Variabilität der abhängigen Variablen liefert, während ein R2-Wert von 1 bedeutet, dass das Regressionsmodell die Variabilität der abhängigen Variablen vollständig erklärt.
Es ist wichtig zu beachten, dass R2 nicht immer ein zuverlässiges Maß für die Vorhersagegenauigkeit eines Regressionsmodells ist, insbesondere wenn das Modell mit neuen Daten getestet wird.
Wie viele Beobachtungen braucht man für eine Regression?
Es gibt keine feste Regel für die Anzahl der Beobachtungen, die für eine Regression erforderlich sind. Die Anzahl der erforderlichen Beobachtungen hängt von verschiedenen Faktoren ab, wie z. B. der Anzahl der unabhängigen Variablen, der Komplexität des Regressionsmodells und der Stärke der Beziehung zwischen den Variablen.
Im Allgemeinen sollten jedoch genügend Beobachtungen vorhanden sein, um eine repräsentative Stichprobe der Daten zu erhalten und um sicherzustellen, dass das Modell ausreichend gut an die Daten angepasst ist. Als Faustregel gilt, dass für jede unabhängige Variable, die in das Modell aufgenommen wird, mindestens 10 Beobachtungen vorliegen sollten. Wenn das Modell jedoch sehr komplex ist oder die Beziehung zwischen den Variablen sehr schwach ist, können mehr Beobachtungen erforderlich sein.
Es ist wichtig zu beachten, dass es nicht immer notwendig ist, so viele Beobachtungen wie möglich zu haben. In manchen Fällen kann es sinnvoller sein, weniger Beobachtungen zu haben, diese aber sorgfältig auszuwählen, um sicherzustellen, dass sie relevant und repräsentativ für die zu untersuchende Population sind.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn