Einleitung normalverteilte Daten
Die NormalverteilungNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. , auch als Gauß’sche Normalverteilung oder Glockenkurve bezeichnet, ist eine wichtige Verteilung in der Statistik und tritt in vielen verschiedenen Anwendungsbereichen auf. Sie beschreibt eine symmetrische Verteilung, bei der die Daten um einen mittleren Wert (dem arithmetischen Mittel) herum verteilt sind. Die Normalverteilung hat einen charakteristischen Verlauf in Form einer Glockenkurve und ist durch zwei Parameter definiert, nämlich dem Erwartungswert (Mittelwert) und der StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. .
Die Normalverteilung tritt häufig bei natürlichen Phänomenen auf und wird daher oft als Modell für die Verteilung von Daten in vielen Bereichen verwendet, z.B. in der Medizin, der Psychologie und der Ökonometrie. Allerdings gibt es auch viele Fälle, in denen die Daten nicht normalverteilt sind, in denen andere Verteilungen besser geeignet sind. Es ist daher wichtig, die Normalverteilung von Daten zu prüfen, bevor man sie analysiert.
In vielen Fällen wird die Annahme einer Normalverteilung als Voraussetzung für die Gültigkeit von Analysemethoden angenommen. Daher ist es wichtig, die Normalverteilung der Daten zu prüfen, bevor man mit der Analyse fortfährt. In SPSS gibt es verschiedene Möglichkeiten, um die Normalverteilung zu prüfen. Dazu gehören zum Beispiel Verteilungstests, die auf die Normalverteilung hin überprüfen, sowie Graphiken wie Histogramme und Q-Q-Plots, die die Verteilung der Daten visualisieren.
In diesem Beitrag werden wir uns mit dem Thema „Normalverteilung prüfen in SPSS“ auseinandersetzen und verschiedene Möglichkeiten vorstellen, wie man in SPSS die Normalverteilung der Daten überprüfen kann. Wir werden dabei auf die verschiedenen Testverfahren und Graphiken eingehen und zeigen, wie man sie in SPSS anwendet und interpretiert. Auch werden wir darauf eingehen, wie man gegebenenfalls mit nicht-normalverteilten Daten umgeht und welche Alternativen es gibt.
Wie prüft man in SPSS auf Normalverteilung?
In SPSS gibt es mehrere Möglichkeiten, um die Normalverteilung von Daten zu prüfen. Eine Möglichkeit ist die Verwendung des „Test auf Normalverteilung“. Dieser Test wird im Menü „Analyse“ unter „Deskriptive Statistiken“ gefunden. Wenn dieser Test ausgewählt wird, kannst du das untersuchende Datenfeld auswählen und SPSS wird dann eine Reihe von Statistiken und Grafiken erstellen, die dazu beitragen, die Normalverteilung der Daten zu untersuchen. In dieser Anleitung werden diesen Prozess Schritt-für-Schritt durchgehen. Darüber hinaus sehen wir uns Diagramme und Plots an.
Zum Testen der Variablen auf Normalverteilung eignen sich die statistischen Prüfverfahren Shapiro-Wilk-Test und der Kolmogorov-Smirnov Test, bei denen ein Signifikanzwert als Ausschlaggebenes Ergebnis (p-WertP-wert Der p-Wert ist ein Maß für die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis oder eine Beobachtung in einer Studie durch Zufall entstanden ist, wenn die Nullhypothese wahr ist. Er wird verwendet, um zu bestimmen, ob ein Ergebnis statistisch signifikant ist und ob es auf einen wirklichen Unterschied oder eine Beziehung zwischen den Variablen hinweist. Der p-Wert gibt an, wie wahrscheinlich es ist, dass das beobachtete Ergebnis auftreten würde, wenn es tatsächlich keinen Unterschied oder keine Beziehung zwischen den Variablen gibt. Ein niedriger p-Wert bedeutet, dass das Ergebnis wahrscheinlich auf einen Unterschied oder eine Beziehung zurückzuführen ist, während ein hoher p-Wert darauf hinweist, dass das Ergebnis wahrscheinlich auf Zufall zurückzuführen ist.) Kriterium herangezogen wird. Beide Verfahren werden wir in dieser Anleitung verwenden.
Wo finde ich den Beispieldatensatz dieser Anleitung?
Hier: Beispieldatensätze
Test auf Normalverteilung in SPSS
In SPSS einen Test auf Normalverteilung durchführen. Inklusive Shapiro-Wilk-Test.
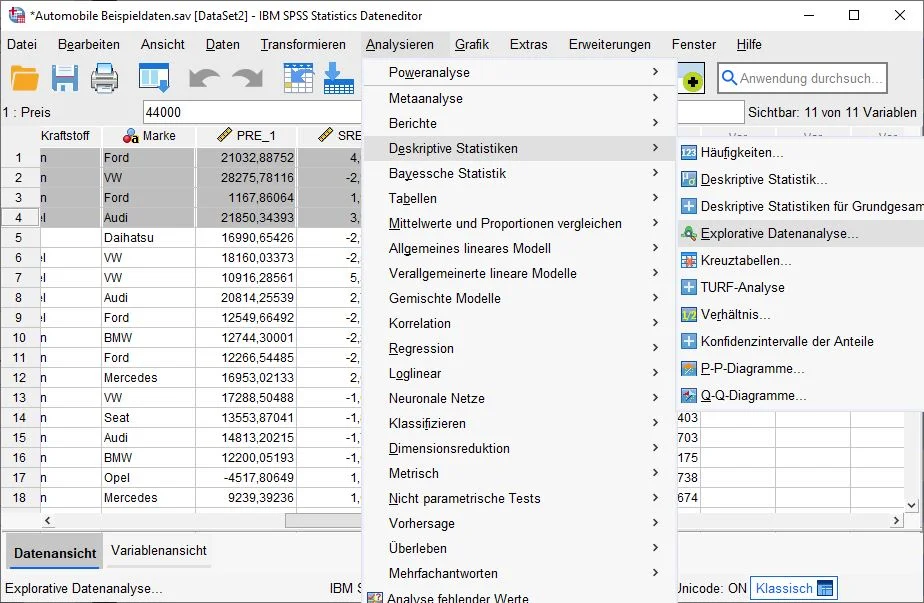
Auswahl im Menü

Wir klicken in SPSS auf die Schaltfläche Analysieren > Deskriptive Statistiken > Explorative Datenanalyse.
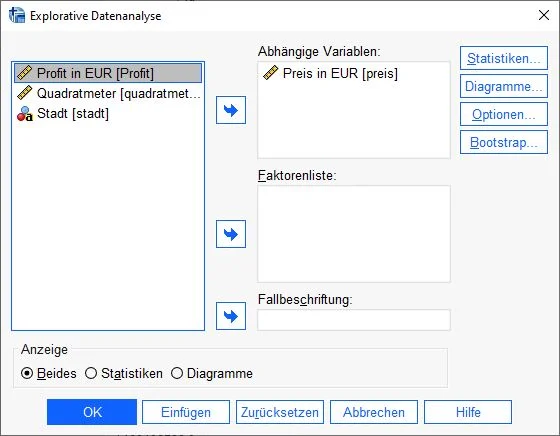
Dialogfenster explorative Datenanalyse in SPSS

Es erscheint das Dialogfenster Explorative Datenanalyse. Links befinden sich alle Variablen des Datensatzes.
Wir ziehen mit Drag-and-Drop die zu untersuchende Variable auf das Feld Abhängige Variablenabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. . Alternativ markieren wir mit einem Klick die Variable und drücken anschließend die Pfeiltaste (grüner Pfeil), um die Variable in das Feld Abhängige Variableabhängige Variable Die abhängige Variable ist die Variable, die in einer Studie gemessen oder beobachtet wird und die von der unabhängigen Variable abhängig ist. Die unabhängige Variable ist die Variable, die in der Studie manipuliert oder gesteuert wird und die vermutete Ursache für die Veränderungen in der abhängigen Variable ist. zu befördern.
Hinweis: Falls dein Datensatz mehrere unterschiedliche Gruppen beinhaltet, kann in diesem Feld die entsprechende Gruppenvariable eingefügt werden. Beispielsweise die Stadt. Diese Variable befindet sich nicht im Datensatz.
Nun klicken wir auf das Feld Statistiken auf der rechten Seite
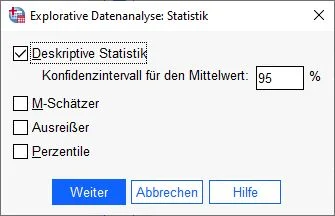
Dialogfenster Explorative Datenanalyse Statistik

Es öffnet sich das Dialogfenster Explorative Datenanalyse: Statistik.
Hier setzen wir einen Haken bei Deskriptive Statistik und klicken auf Weiter.
Auswahl von Diagrammen

Nun klicken wir auf das Feld Diagramme auf der rechten Seite.
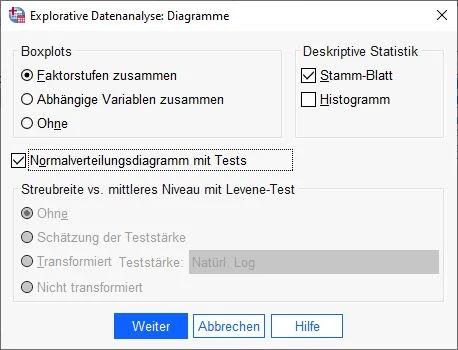
Dialogfenster: Explorative Datenanalyse Diagramme

Es öffnet sich das Dialogfenster Diagramme, wo wir im Feld Deskriptive Statistik die Option Histogramm und setzen einen Hacken bei Normalverteilungsdiagramm mit Tests.
Wir bestätigen unsere Eingaben mit einem Klick auf Weiter.
Bereit zum Starten der Analyse auf Normalverteilung in SPSS

Abschließend klicken zum Bestätigen auf OK und schauen uns im nächsten Schritt die Ausgabe an.
Interpretation der Ausgaben in SPSS
SPSS zeigt uns an dieser Stelle viele Tabellen. Zunächst zeigt uns die Tabelle Descriptives (Deskriptive Statistiken) eine Übersicht an Kennzahlen. Hier interessieren wir uns für die Schiefe (Skewness) und Kurtosis.
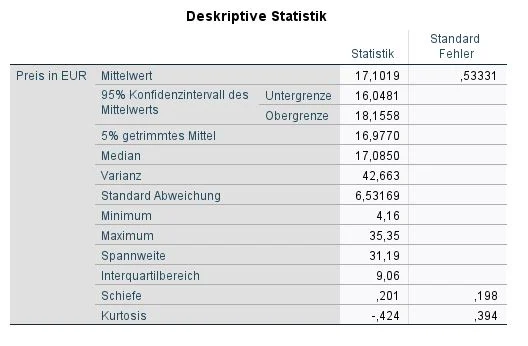
Wenn beide Werte den Wert 0 aufweisen, kann eine Normalverteilung angenommen werden. Dies ist jedoch nur ein theoretischer Wert. In echten Experimenten können beide Werte größer oder kleiner als Null sein.
Als Regel gilt, dass die Werte nicht größer als 1 und nicht kleiner als -1 sein dürfen, um von einer Normalverteilung auszugehen.
In unserem Beispiel hat die Kennzahl Größe eine Schiefe (Skewness) von .201 und Kurtosis von -.424. Die Zahlen deuten auf eine Normalverteilung der Ergebnisse hin.
Erklärung Kurtosis

Die Kurtosis gibt an, wie weit die Randbereiche einer Verteilung von der Normalverteilung abweichen. Durch die Kurtosis können Sie ein erstes Verständnis der allgemeinen Merkmale der Verteilung Ihrer Daten erlangen.
Daten, die perfekt einer Normalverteilung folgen, weisen den Kurtosis-Wert 0 auf. Normalverteilte Daten bilden die Basislinie für die Kurtosis. Wenn die Kurtosis einer Stichprobe wesentlich von 0 abweicht, kann dies darauf hinweisen, dass die Daten nicht normalverteilt sind.
Ein positiver Kurtosis-Wert für eine Verteilung deutet darauf hin, dass sich die Verteilung durch stärker ausgeprägte Randbereiche als die Normalverteilung auszeichnet. Daten, die einer t-Verteilung folgen, weisen beispielsweise einen positiven Kurtosis-Wert auf. Die durchgezogene Linie stellt die Normalverteilung und die gepunktete Linie eine Verteilung mit einem positiven Kurtosis-Wert dar.
Ein negativer Kurtosis-Wert für eine Verteilung deutet darauf hin, dass sich die Verteilung durch schwächer ausgeprägte Randbereiche als die Normalverteilung auszeichnet. Daten, die einer Betaverteilung folgen, deren erster und zweiter Formparameter gleich 2 ist, weisen beispielsweise einen negativen Kurtosis-Wert auf. Die durchgezogene Linie stellt die Normalverteilung und die gepunktete Linie eine Verteilung mit einem negativen Kurtosis-Wert dar.
Erklärung Schiefe – Skewness

Die Schiefe gibt das Ausmaß an, in dem die Daten asymmetrisch sind. Der Schiefewert – 0, positiv oder negativ – liefert Informationen über die Form der Daten. Mit zunehmender Symmetrie der Daten nähert sich deren Schiefewert null an. Abbildung A zeigt normalverteilte Daten, die per definitionem eine relativ geringe Schiefe aufweisen. Wenn Sie eine Linie durch die Mitte dieses Histogramms von normalverteilten Daten zeichnen, wird ersichtlich, dass die beiden Seiten einander spiegeln. Eine fehlende Schiefe allein impliziert jedoch keine Normalverteilung. Abbildung B zeigt eine Verteilung, bei der beide Seiten einander immer noch spiegeln, die Daten jedoch keineswegs normalverteilt sind.
Positiv schiefe oder rechtsschief verteilte Daten werden so bezeichnet, weil der Randbereich der Verteilung nach rechts zeigt und der Schiefewert größer als 0 (d. h. positiv) ist. Gehaltsdaten weisen häufig eine solche Schiefe auf: Viele Mitarbeiter eines Unternehmens erhalten ein relativ kleines Gehalt, während zunehmend weniger Personen sehr hohe Gehälter beziehen. Linksschiefe oder negativ schiefe Daten werden so bezeichnet, weil der Randbereich der Verteilung nach links weist und ein negativer Schiefewert vorliegt. Daten zu Ausfallraten sind häufig linksschief. Ein Beispiel sind Glühlampen: Sehr wenige brennen sofort durch, und die überwiegende Mehrzahl weist eine lange Lebensdauer auf.
Test auf Normalverteilung mit dem Shapiro-Wilk-Test in SPSS
Die Normalverteilung kann anhand des Shapiro-Wilk-Test bestimmt werden. Nach der Berechnung oben finden wir die Ergebnisse in der Ausgabe in SPSS.
Was ist der Shapiro-Wilk-Test?
Der Shapiro-Wilk-Test ist ein statistischer Test, der verwendet wird, um zu prüfen, ob ein gegebener Datensatz normalverteilt ist oder nicht. Er wurde von Samuel Shapiro und Martin Wilk entwickelt und gehört zu den am häufigsten verwendeten Tests zur Überprüfung der Normalverteilung von Daten.
Der Test basiert auf dem Vergleich der Empirischen Verteilungsfunktion (ECDF) der Daten mit der Theoretischen Verteilungsfunktion einer Normalverteilung. Wenn die beiden gut übereinstimmen, deutet dies darauf hin, dass die Daten normalverteilt sind. Wenn sie jedoch signifikant unterschiedlich sind, deutet dies darauf hin, dass die Daten nicht normalverteilt sind.

Hierzu richten wir unsere Aufmerksamkeit auf die Tabelle „Test auf Normalverteilung“ (Tests of Normality). In der ersten Spalte werden die untersuchten Variablen aufgelistet. Die letzte Spalte zeigt den Signifikanzwert des Shapiro-Wilk-Tests. Jeder Wert über 0,05 weißt auf eine Normalverteilung hin. Doch Vorsicht: Der Shapiro-Wilk-Test neigt bei größeren Stichproben dazu, überkritisch zu sein und NormalverteilungenNormalverteilung Die Normalverteilung, auch Gauss-Verteilung genannt, ist eine Art von Verteilung, bei der die Werte einer Variablen symmetrisch um den Mittelwert angeordnet sind und die Wahrscheinlichkeit, dass Werte in bestimmten Bereichen auftreten, durch eine Glockenkurve dargestellt wird. zu verneinen, selbst wenn sie eigentlich angenommen werden können.
In unserem Beispiel ist die Variable Preis in EUR (.150) normalverteilt. Die Variable Preis in EUR ist nicht signifikant und deshalb normalverteilt.
Warum gibt es zwei Spalten mit Signifikanzen? SPSS berechnet die Signifikanzen anhand des Kolmogorov-Smirnov-Test und des Shapiro-Wilk-Test. Im Gegensatz zum Kolmogorov-Smirnov-Test besitzt der Shapiro-Wilk-Test eine höhere PowerStatistische Power Statistische Power ist die Wahrscheinlichkeit, dass ein statistisches Testverfahren einen wirklich vorhandenen Unterschied zwischen zwei Gruppen oder Bedingungen erkennen wird. Eine hohe statistische Power bedeutet, dass das Testverfahren empfindlich genug ist, um kleine Unterschiede zu erkennen, während eine niedrige statistische Power dazu führen kann, dass wichtige Unterschiede übersehen werden. Es ist wichtig, dass die statistische Power bei der Planung einer Studie berücksichtigt wird, um sicherzustellen, dass das Testverfahren ausreichend empfindlich ist, um wichtige Unterschiede zu erkennen. , weshalb dieser in der Regel verwendet werden sollte.
Was ist der Kolmogorov-Smirnov-Test?
Die Prüfung auf Normalverteilung anhand des Kolmogorov-Smirnov-Test ist dem Shapiro-Wilk-Test nicht unähnlich. Die Ausgabe befindet sich in der gleichen Tabelle. In der Regel wird der Kolmogorov-Smirnov-Test dann verwendet, wenn die Stichprobengröße sehr groß ist (N>5000). Für gewöhnlich sollte deshalb der Shapiro-Wilk-Test verwendet werden.
Prüfung der Normalverteilung: Diagramme
Histogramme
Ein Histogramm stellt die Häufigkeiten innerhalb der Variable mit Säulen dar. Größe wieder. Dies entspricht der Normalverteilung.
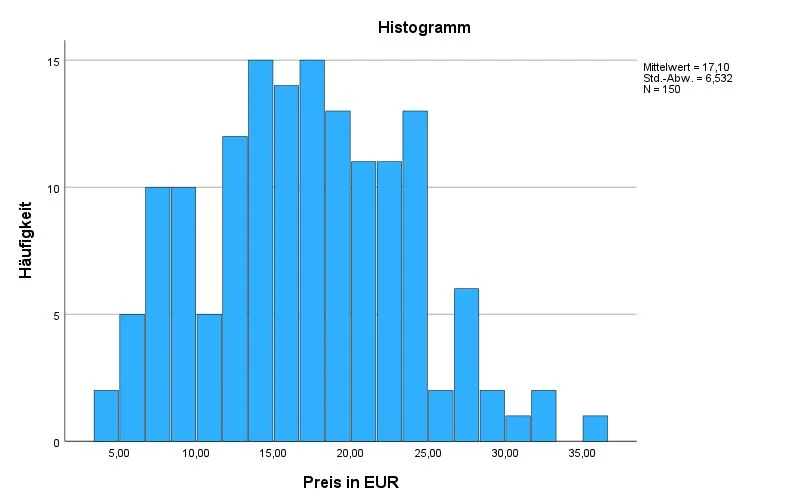
In unserem Beispiel liegen die meisten Preise in etwa der Mitte. Je extremer Werte nach unten oder oben werden, desto seltener finden sich Werte in dem Datensatz.
Was ist ein Histogramm?
Ein Histogramm ist ein Diagramm, das verwendet wird, um die Häufigkeit von Daten in bestimmten Bereichen oder Klassen darzustellen. Es besteht aus einer Reihe von vertikalen Säulen, die die Häufigkeit von Daten in bestimmten Klassenbereichen darstellen. Die Klassenbereiche werden auf der horizontalen Achse aufgeführt und die Häufigkeit der Daten wird auf der vertikalen Achse dargestellt.
Histogramme eignen sich besonders gut für die Darstellung von Daten, die in einem bestimmten Bereich konzentriert sind oder die eine bestimmte Form oder Struktur aufweisen, wie z.B. die Verteilung von Alter oder Gehalt in einer bestimmten Bevölkerungsgruppe. Sie können auch verwendet werden, um Verteilungen von Daten zu vergleichen oder um die Normalverteilung von Daten zu untersuchen.
QQ-Plots
Eine weitere Möglichkeit die Daten grafisch auf eine Normalverteilung zu überprüfen sind die QQ-Plot Diagramme.
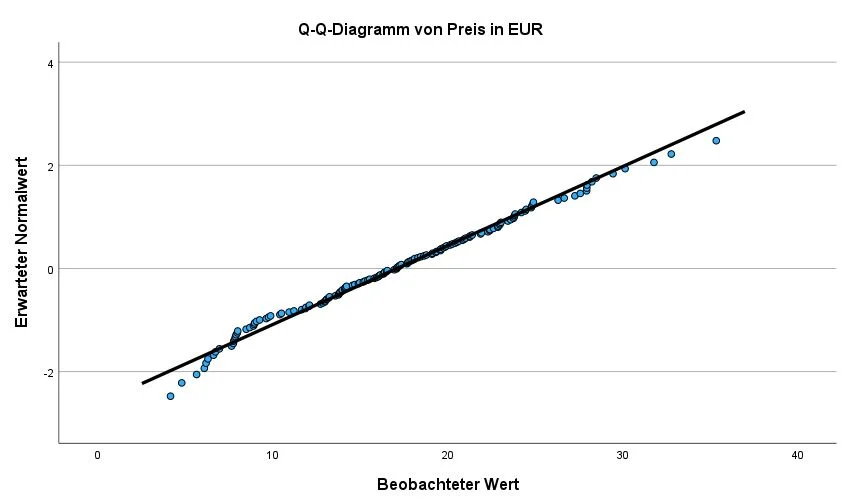
Die Daten sind normalverteilt, wenn sich die Punkte auf der Linie befinden. Wenn sich die Punkte von der eingezeichneten Linie abweichen, können wir von Ausreißern ausgehen. Wenn die Verteilung einer Treppe (mit mehreren Ebenen) gleicht, sind im Datensatz gerundete oder diskrete Daten vorhanden.
In unserem Beispiel deutet der QQ-Plot der Variable Preis in EUR auf eine Normalverteilung hin. Die Werte sind sehr nah an der Linie. Lediglich bei den extremen Werten gibt es kleinere Abweichungen.
Was ist ein QQ-Plot?
Ein Q-Q-Plot, auch als Quantile-Quantile-Plot bezeichnet, ist ein Diagramm, das verwendet wird, um die Verteilung von Daten mit einer Normalverteilung zu vergleichen. Es wird häufig verwendet, um die Normalverteilung von Daten zu prüfen oder um die Verteilung von Daten mit einer bekannten Normalverteilung zu vergleichen.
Ein Q-Q-Plot besteht aus zwei Achsen, die die Quantile der Daten darstellen. Die Quantile sind die Werte, die eine bestimmte Häufigkeit der Daten darstellen. Zum Beispiel sind die mittleren 50% der Daten die Quantile, die die Medianwerte darstellen.
Ergebnisse beschreiben
Die Variable Preis in EUR waren gemäß dem Shapiro-Wilk-Test normalverteilt.
5 Fakten zur Normalverteilung
- Die Normalverteilung ist eine wichtige Verteilung in der Statistik und tritt in vielen Anwendungsbereichen auf. Sie beschreibt eine symmetrische Verteilung, bei der die Daten um einen mittleren Wert (dem arithmetischen Mittel) herum verteilt sind.
- Die Normalverteilung hat einen charakteristischen Verlauf in Form einer Glockenkurve und ist durch zwei Parameter definiert, nämlich dem Erwartungswert (Mittelwert) und der Standardabweichung.
- In vielen Fällen wird die Annahme einer Normalverteilung als Voraussetzung für die Gültigkeit von Analysemethoden angenommen. Daher ist es wichtig, die Normalverteilung der Daten zu prüfen, bevor man mit der Analyse fortfährt.
- Es gibt verschiedene Möglichkeiten, um die Normalverteilung zu prüfen, darunter Verteilungstests und Grafiken wie Histogramme und Q-Q-Plots.
- Wenn die Daten nicht normalverteilt sind, gibt es alternative Analysemethoden, die für nicht-normalverteilte Daten geeignet sind. Es ist wichtig, die Art der Verteilung der Daten zu berücksichtigen, um die geeignete Analysemethode
Häufig gestellte Fragen und Antworten: Normalverteilung in SPSS überprüfen
Wie prüft man auf Normalverteilung?
In SPSS gibt es mehrere Möglichkeiten, um die Normalverteilung von Daten zu prüfen. Eine Möglichkeit ist die Verwendung des „Normalverteilungstests“. Dieser Test wird im Menü „Analyse“ unter „Deskriptive Statistiken“ gefunden. Wenn Sie diesen Test auswählen, können Sie das zu untersuchende Datenfeld auswählen und SPSS wird dann eine Reihe von Statistiken und Grafiken erstellen, die dazu beitragen, die Normalverteilung der Daten zu untersuchen.
Eine weitere Möglichkeit ist die Verwendung von Normalverteilungs-Plots. Diese Plots können im Menü „Graph“ unter „Diagramme“ gefunden werden. Wenn Sie einen Normalverteilungs-Plot erstellen, können Sie das zu untersuchende Datenfeld auswählen und SPSS wird eine Normalverteilungskurve über den tatsächlichen Datenwerte plotten. Dies kann dabei helfen, die Normalverteilung visuell zu bestätigen oder zu verwerfen.
Es gibt auch andere Tests und Methoden, die in SPSS verwendet werden können, um die Normalverteilung von Daten zu prüfen, wie z.B. den Q-Q Plot oder den Anderson-Darling Test. Es ist wichtig zu beachten, dass kein Test perfekt ist und dass es in der Regel auf mehrere Tests und Methoden ankommt, um eine zuverlässige Einschätzung der Normalverteilung von Daten zu erhalten.
Was tun, wenn Daten nicht normalverteilt sind SPSS?
Wenn du feststellst, dass deine Daten nicht normalverteilt sind, gibt es einige Dinge, die du in SPSS tun kannst, um die Daten trotzdem zu analysieren. Hier sind einige Möglichkeiten:
Verwende nichtparametrische Tests: Wenn Daten nicht normalverteilt sind, können nichtparametrische Tests anstelle von parametrischen Tests verwenden werden. Diese Tests sind weniger anspruchsvoll hinsichtlich der Annahmen über die Verteilung der Daten und können daher bei nicht normalverteilten Daten nützlich sein. Sie finden nichtparametrische Tests in SPSS im Menü „Analyse“ unter „Nonparametrische Tests“.
Transformiere die Daten: In manchen Fällen können die Daten transformiert werden, um sie normalverteilter zu machen. Zum Beispiel können die Daten logarithmiert oder sie in Quadratwurzeln genommen werden. Diese Transformationen können die Verteilung der Daten verändern und sie normalverteilter machen.
Verwende robustere Statistiken: In manchen Fällen können Sie robustere Statistiken verwenden, die weniger anfällig für AusreißerAusreißer Ausreißer sind Datenpunkte, die deutlich von den übrigen Daten abweichen und die Verteilung der Daten beeinflussen können. Sie können aufgrund von Messfehlern, ungewöhnlichen Ereignissen oder menschlichem Fehler auftreten und sollten in der Regel in der Analyse berücksichtigt werden, um sicherzustellen, dass die Ergebnisse valide sind. und nicht normalverteilte Daten sind. Zum Beispiel können Mediane statt Mittelwerte verwendet werden und die Mediane-Absolut-Abweichung statt der Standardabweichung.
Verwende andere Verteilungen: In manchen Fällen können andere Verteilungen als die Normalverteilung verwendet werden, um die Daten zu analysieren. Zum Beispiel könnte eine t-Verteilung oder eine Cauchy-Verteilung verwendet werden, wenn die Daten lange Schwanzverteilungen aufweisen.
Es ist wichtig zu beachten, dass keine dieser Optionen perfekt ist und dass es in der Regel auf mehrere Faktoren ankommt, um die beste Vorgehensweise für die Analyse von nicht normalverteilten Daten zu bestimmen. Ein guter Ausgangspunkt ist es, zunächst zu versuchen, die Normalverteilung der Daten zu verbessern, indem man Transformationen oder robustere Statistiken verwendet. Wenn dies nicht möglich ist, können Sie nichtparametrische Tests oder andere Verteilungen in Betracht ziehen.
Wann welcher Test auf Normalverteilung?
Es gibt viele Tests, die verwendet werden können, um die Normalverteilung von Daten zu prüfen. Welcher Test am besten geeignet ist, hängt von verschiedenen Faktoren ab, wie der Größe der Stichprobe, der Form der Verteilung und dem verfügbaren Softwarepaket. Hier sind einige allgemeine Richtlinien zur Auswahl von Tests zur Prüfung der Normalverteilung:
– Wenn du eine kleine bis mittelgroße Stichprobe hast und einen einfach zu verwendenden Test möchtest, könntest du den Normalverteilungstest verwenden. Dieser Test ist in SPSS verfügbar und berechnet auch Statistiken und erstellt ein Histogramm und einen Normalverteilungs-Plot, um die Normalverteilung visuell zu bestätigen oder zu verwerfen. Siehe diese Anleitung.
– Wenn du eine kleine bis mittelgroße Stichprobe hast und einen genauen Test möchtest, könntest du den Shapiro-Wilk-Test verwenden. Dieser Test ist einer der genauesten Tests zur Prüfung der Normalverteilung, aber beachte, dass er in manchen Softwarepaketen nicht verfügbar ist.
– Wenn du eine Stichprobe jeglicher Größe hast und einen etwas genaueren Test möchtest, könntest du den Anderson-Darling-Test verwenden. Dieser Test kann für Stichproben jeglicher Größe verwendet werden, aber beachte, dass er für unerfahrene Benutzer schwieriger zu interpretieren sein kann.
– Wenn du eine visuelle Methode zur Prüfung der Normalverteilung möchtest, die für Stichproben jeglicher Größe geeignet ist, könntest du Q-Q-Plots verwenden. Diese Plots sind in vielen Softwarepaketen verfügbar und einfach zu interpretieren, aber beachte, dass sie weniger genau als andere Tests
Welche Variablen auf Normalverteilung testen?
Es gibt keine definitive Antwort darauf, welche Variablen auf Normalverteilung getestet werden sollten, da dies von der Art der Studie und der verwendeten Analysemethoden abhängt. In der Regel werden jedoch die folgenden Überlegungen berücksichtigt:
– Wenn du parametrische Tests verwenden möchtest, solltest du die Normalverteilung von den Variablen prüfen, die als Ausgangsvariablen in diesen Tests verwendet werden. Diese Tests setzen voraus, dass die Daten normalverteilt sind, und können unzuverlässige Ergebnisse liefern, wenn die Daten nicht normalverteilt sind.
– Wenn du die Verteilung von Merkmalen oder Eigenschaften in deiner Stichprobe untersuchen möchtest, solltest du die Normalverteilung von diesen Variablen prüfen. Dies kann beispielsweise bei der Untersuchung von Alter, Geschlecht oder Bildungsniveau der Fall sein.
– Wenn du die Beziehung zwischen verschiedenen Variablen untersuchen möchtest, solltest du die Normalverteilung von beiden Variablen prüfen. Dies ist insbesondere wichtig, wenn du KorrelationenKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird. oder Regressionsanalysen durchführen möchtest.
Es ist wichtig zu beachten, dass die Normalverteilung von Variablen nicht immer erforderlich ist, um wichtige Erkenntnisse aus deiner Studie zu gewinnen. Wenn deine Daten nicht normalverteilt sind, gibt es auch andere Methoden.
Wann benutzt man Kolmogorov Smirnov Test?
Der Kolmogorov-Smirnov-Test ist ein nicht-parametrischer Test, der verwendet wird, um zu überprüfen, ob eine gegebene Stichprobe von Daten aus einer bestimmten Verteilung stammt. Er wird oft verwendet, wenn man nicht viel über die Verteilung der Daten weiß oder wenn die Daten keine Normalverteilung haben.
Ein Beispiel dafür, wann man den Kolmogorov-Smirnov-Test verwenden könnte, ist, wenn man überprüfen möchte, ob die Größen von Teilen, die in einer Fabrik hergestellt werden, einer bestimmten Größenverteilung entsprechen. Man könnte die Größen der Teile messen und den Kolmogorov-Smirnov-Test verwenden, um zu überprüfen, ob die Größenverteilung der Teile mit der erwarteten Verteilung übereinstimmt.
Es gibt viele andere Anwendungsfälle für den Kolmogorov-Smirnov-Test. Er wird häufig in der Statistik und in vielen anderen Bereichen eingesetzt, in denen man die Verteilung von Daten überprüfen möchte.
Welcher Test wenn nicht normalverteilt?
Wenn die Daten keine Normalverteilung haben, gibt es einige Tests, die man stattdessen verwenden kann. Eine Möglichkeit wäre der Kolmogorov-Smirnov-Test, der erwähnt wurde. Dies ist ein nicht-parametrischer Test, der verwendet wird, um zu überprüfen, ob eine gegebene Stichprobe von Daten aus einer bestimmten Verteilung stammt. Er wird oft verwendet, wenn man nicht viel über die Verteilung der Daten weiß oder wenn die Daten keine Normalverteilung haben.
Ein weiterer Test, der verwendet werden kann, wenn die Daten keine Normalverteilung haben, ist der Wilcoxon-Mann-Whitney-Test. Dies ist auch ein nicht-parametrischer Test, der verwendet wird, um zu überprüfen, ob zwei Stichproben von Daten aus der gleichen Verteilung stammen. Er wird oft verwendet, wenn die Stichproben nicht normalverteilt sind oder wenn die Stichproben sehr unterschiedlich in Größe sind.
Es gibt noch viele andere Tests, die man verwenden kann, wenn die Daten keine Normalverteilung haben. Welcher Test am besten geeignet ist, hängt von den spezifischen Eigenschaften der Daten und der Frage ab, die man beantworten möchte. Es ist wichtig, sich bewusst zu machen, dass die Annahme der Normalverteilung bei vielen statistischen Tests eine Annahme ist, die oft nicht in der realen Welt gilt. Es ist daher wichtig, die Verteilung der Daten zu überprüfen und geeignete Tests zu verwenden, wenn die Normalverteilung nicht angenommen werden kann.
Wann verwendet man Mann Whitney U Test?
Der Wilcoxon-Mann-Whitney-Test, auch als Mann-Whitney-U-Test bekannt, ist ein nicht-parametrischer Test, der verwendet wird, um zu überprüfen, ob zwei Stichproben von Daten aus der gleichen Verteilung stammen. Er wird oft verwendet, wenn die Stichproben nicht normalverteilt sind oder wenn die Stichproben sehr unterschiedlich in Größe sind.
Ein Beispiel dafür, wann man den Mann-Whitney-U-Test verwenden könnte, ist, wenn man überprüfen möchte, ob es einen Unterschied in den durchschnittlichen Verkaufszahlen zwischen zwei verschiedenen Warensorten gibt. Man könnte die Verkaufszahlen für jede Warensorte messen und den Mann-Whitney-U-Test verwenden, um zu überprüfen, ob es einen statistisch signifikanten Unterschied zwischen den Verkaufszahlen der beiden Warensorten gibt.
Es gibt viele andere Anwendungsfälle für den Mann-Whitney-U-Test. Er wird häufig in der Statistik und in vielen anderen Bereichen eingesetzt, in denen man überprüfen möchte, ob zwei Stichproben von Daten aus der gleichen Verteilung stammen. Wie bei jedem statistischen Test ist es wichtig, dass man die Annahmen des Tests versteht und sicherstellt, dass der Test für die spezifischen Daten und die Fragestellung geeignet ist.
Welche KorrelationKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird. wenn keine Normalverteilung?
Wenn die Daten keine Normalverteilung haben, könnte man in Betracht ziehen, stattdessen eine nicht-parametrische Korrelationsmethode zu verwenden. Eine solche Methode wäre zum Beispiel der Spearman-Rangkorrelationskoeffizient.
Der Spearman-Rangkorrelationskoeffizient ist eine nicht-parametrische Methode zur Messung der Korrelation zwischen zwei Variablen. Im Gegensatz zum Pearson-Korrelationskoeffizienten, der für die Berechnung der Korrelation zwischen normalverteilten Variablen verwendet wird, kann der Spearman-Rangkorrelationskoeffizient verwendet werden, um die Korrelation zwischen Variablen jeglicher Verteilung zu messen.
Ein Beispiel dafür, wann man den Spearman-Rangkorrelationskoeffizienten verwenden könnte, ist, wenn man überprüfen möchte, ob es eine Korrelation zwischen der Größe von Unternehmen und ihrem finanziellen Erfolg gibt. Man könnte die Größe der Unternehmen anhand ihrer Anzahl von Mitarbeitern messen und den finanziellen Erfolg anhand ihres Gewinns. Wenn die Daten keine Normalverteilung haben, könnte man den Spearman-Rangkorrelationskoeffizienten verwenden, um zu überprüfen, ob es eine Korrelation zwischen diesen beiden Variablen gibt.
Es gibt viele andere nicht-parametrische Korrelationsmethoden, die man verwenden könnte, wenn die Daten keine Normalverteilung haben. Welche Methode am besten geeignet ist, hängt von den spezifischen Eigenschaften der Daten und der Fragestellung ab. Es ist wichtig, sich bewusst zu machen, dass die Annahme der Normalverteilung bei vielen statistischen Tests und Methoden eine Annahme ist, die oft nicht in der realen Welt gilt. Es ist daher wichtig, die Verteilung der Daten zu überprüfen und geeignete Methoden zu verwenden, wenn die Normalverteilung nicht angenommen werden kann.
Wann Shapiro Wilk oder Kolmogorov Smirnov?
Der Shapiro-Wilk-Test und der Kolmogorov-Smirnov-Test sind beide Tests, die verwendet werden, um zu überprüfen, ob eine gegebene Stichprobe von Daten aus einer Normalverteilung stammt. Der Shapiro-Wilk-Test ist ein parametrischer Test, der davon ausgeht, dass die Daten normalverteilt sind, während der Kolmogorov-Smirnov-Test ein nicht-parametrischer Test ist, der für Daten jeglicher Verteilung geeignet ist.
Wann man den Shapiro-Wilk-Test oder den Kolmogorov-Smirnov-Test verwendet, hängt von der Verteilung der Daten und der Fragestellung ab. Wenn man davon ausgeht, dass die Daten normalverteilt sind und genügend Beobachtungen hat (in der Regel mehr als 50 Beobachtungen), dann könnte man den Shapiro-Wilk-Test verwenden. Wenn man nicht davon ausgehen kann, dass die Daten normalverteilt sind oder weniger als 50 Beobachtungen hat, dann könnte man stattdessen den Kolmogorov-Smirnov-Test verwenden.
Es ist wichtig zu beachten, dass die Annahme der Normalverteilung bei vielen statistischen Tests eine Annahme ist, die oft nicht in der realen Welt gilt. Es ist daher wichtig, die Verteilung der Daten zu überprüfen und geeignete Tests zu verwenden, wenn die Normalverteilung nicht angenommen werden kann.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn