Was ist die Reliabilitätsanalyse?
Die Reliabilitätsanalyse gibt darüber Auskunft, wie verlässlich eine Analyse ist. Sie beschreibt das Ausmaß, inwieweit ein Verfahren bei wiederholter Durchführung identisch misst. Wenn ich mein Experiment ein zweites Mal durchführen werde, kommen dann vergleichbare Ergebnisse heraus? Wenn die Antwort „Nein“ lautet heißt es: wir haben ein Problem.
Eine perfekte Reliabilität wiederum meint, dass ein Messung (Experiment, Fragebogen) stets die identischen Ergebnisse produzieren würde, solange sich die Bedingungen nicht ändern. Eine niedrige Reliabilität verursacht unterschiedliche Ergebnisse bei gleichen Bedingungen.
Was ist der Cronbachs Alpha bei der Reliabilitätsanalyse?
Cronbach’s Alpha ist ein gängiger Reliabilitätskoeffizient, der verwendet wird, um die interne Konsistenz oder Reliabilität von Messungen zu beurteilen. Es wird häufig verwendet, um die Reliabilität von Skalen oder Fragebögen zu messen, die aus mehreren Items bestehen. Cronbach’s Alpha berechnet sich aus dem Korrelationskoeffizienten zwischen den Items einer Skala und gibt einen Wert zwischen 0 und 1 an, wobei ein höherer Wert für eine höhere Reliabilität steht.
Es gibt jedoch einige Einschränkungen bei der Verwendung von Cronbach’s Alpha, insbesondere bei der Beurteilung von Skalen mit wenigen Items oder wenn die Items nicht gut miteinander korrelieren. Trotzdem ist Cronbach’s Alpha ein nützliches Werkzeug, um die interne Konsistenz von Messungen zu beurteilen und kann in vielen Disziplinen hilfreich sein. In dieser Einleitung verwenden wir den Cronbachs Alpha.
Wo finde ich die Beispieldaten für diese Anleitung?
Die Beispieldaten gibt es hier: Beispieldaten
Reliabilität mit SPSS und Cronbachs Alpha berechnen
Reliabilität mit SPSS und Cronbachs Alpha berechnen
Auswahl der Reliabilitätsanalyse im Menü

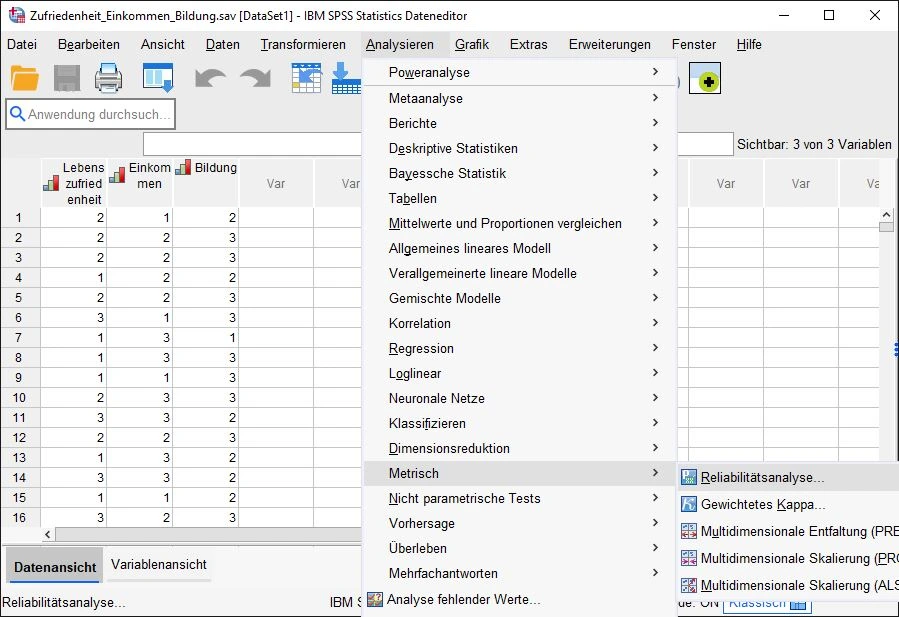
Wir klicken auf Analysieren > Metrisch > Reliabiliätsanalyse
Hinweis: In älteren Version können die Bezeichnungen abweichen. Beispielsweise so: Analysieren > Skala > Reliabilitätsanalyse
Dialogfenster Reliabilitätsanalyse

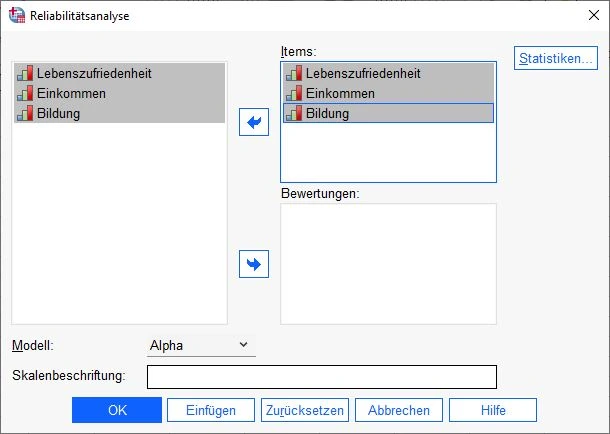
Im Dialogfenster sehen wir zwei Spalten. Links befinden sich die im Datensatz zur Verfügung stehenden Variablen.
Wir ziehen die Variablen, die wir für die Berechnung verwenden möchten, in das rechte Feld Items.Anschließend klicken wir im Fenster auf der rechten Seite auf den Knopf Statistiken.
Statistiken einstellen

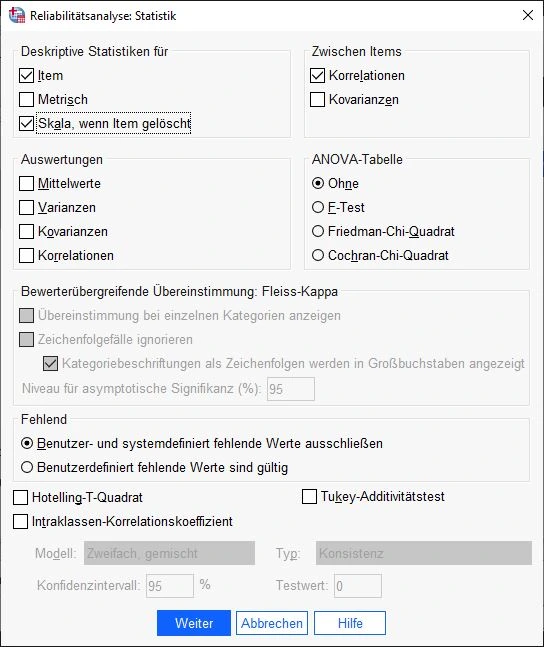
Wir klicken im Feld Deskriptive Statistiken für auf die Optionen
– Item
– Skala wenn Item gelöscht.
Im Feld Zwischen Items wählen wir KorrelationenKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird..Anschließend bestätigen wir die Eingaben mit einem Klick auf die Schaltfläche Weiter.
Bereit zum Starten

Anschließend bestätigen wir die Eingaben mit einem Klick auf die Schaltfläche Weiter.
Ausgabe interpretieren
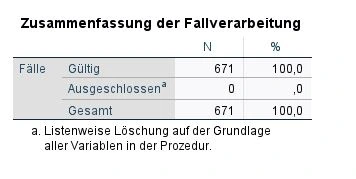
SPSS gibt uns nun mehrere Tabellen, die wir analysieren werden. Beginnen wir mit den gültigen Fällen in der Tabelle Zusammenfassung der Fallverarbeitung. In unserem Beispiel wurde kein Fall ausgeschlossen und alle Fälle (Cases) sind valide, N=671.
Reliabilitätsstatistiken Cronbachs Alpha
Kommen wir zur wichtigsten Tabelle: die Ausgabe vom Cronbachs Alpha. In der ersten Spalte „Cronbachs Alpha“ steht der Wert .751, in der zweiten Spalte erkennen wir das aus Korrelationen berechnete Cronbachs Alpha, in Spalte drei steht die Anzahl der Items geschrieben (das ist die Anzahl der untersuchten Variablen).
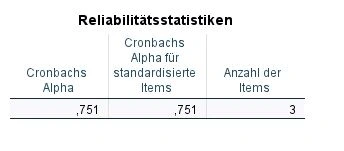
Was machen wir mit dem Ergebnis? Generell gilt, je höher der Cornbach´s Alpha Wert, desto besser. Welche Qualität der Cronbach´s Alpha Wert hat, entnehmen wir folgender Tabelle:
| Chronbach´s Alpha | Bewertung | Empfehlung |
|---|---|---|
| > 0.9 | exzellent | ✔ |
| > 0.8 | gut oder hoch | ✔ |
| > 0.7 | akzeptabel | ⚠ |
| > 0.6 | fragwürdig | ⛔ |
| > 0.5 | schlecht | ⛔ |
| ≤ 0.5 | inakzeptabel | ⛔ |
Diese Tabelle hilft bei der Bewertung des Cornbach´s Alpha. Alles unter 0.5 solltest du in keinem Fall verwenden.
Diese Tabelle gibt eine Übersicht zur Interpretation des Cronbach´s Alpha. In unserem Beispieldatensatz liegt bei .0751 und laut der Tabelle mit „akzeptabel“ bewertet. Je größer der Wert, desto besser. Alles unter .5 ist zu wenig und alles unter .8 kann zumindest kritisch diskutiert werden.
Wie kann der Cronbach´s Alpha Wert erhöht werden?
Es gibt mehrere Wege, den Cronbach´s Alpha Wert zu erhöhen. Reliabilitätsanalysen mit besonders vielen Variablen, neigen zu höheren Cronbach´s Alpha Werten. Darüber hinaus kann es sinnvoll sein, besonders „schwache Items“ aus der Berechnung auszuschließen, um den Wert zu erhöhen. Wie das geht, steht weiter unten in dieser Anleitung.
Vorsicht: Es ist nicht das Ziel der Statistik, möglichst wünschenswerte Zahlen zu produzieren. Künstlich Daten so darzustellen, dass irgendwie ein akzeptables Ergebnis entsteht, sollte nicht deine Motivation sein. Wir möchten die Wahrheit aus deinem Datensatz finden und nichts beschönigen.
Was bedeutet ein negativer Cronbach´s Alpha
Manchmal gibt die Analyse einen negativen Cronbach´s Alpha wert aus, was nicht gut ist. Falls das passiert, sollten wir uns nochmal die Inter-Item-Korrelationsmatrix genauer anschauen. Vielleicht haben wir vergessen, Items zu invertieren. Das heißt, dass verneinte Fragestellungen im Datensatz nicht geändert wurden oder Items im Datensatz sind, die etwas Gegensätzliches aussagen.
Itemstatistiken
Nächster Schritt. Wir betrachten die Übersichtstabelle mit dem Namen „Itemstatistiken“. Wir sehen die Spalten Mittelwert (Mean), StandardabweichungStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. (Std. DeviationStandardabweichung Die Standardabweichung ist ein Maß für die Streuung der Werte einer Variablen um ihren Mittelwert und gibt an, wie sehr die Werte von ihrem Durchschnitt abweichen. Sie wird häufig verwendet, um die Varianz innerhalb einer Population oder Stichprobe zu beschreiben und kann verwendet werden, um die Normverteilung einer Variablen zu beschreiben. Eine kleine Standardabweichung bedeutet, dass die Werte der Variablen dicht um ihren Mittelwert clustern, während eine große Standardabweichung darauf hinweist, dass die Werte der Variablen weiter verteilt sind. ; SD) und Anzahl von Fällen (Untersuchungseinheiten, Cases, N).
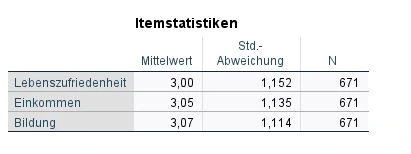
Mit einem Blick auf diese Tabelle erkennen wir das durchschnittliche Antwortverhalten für jede Frage. Wir behalten unsere verwendete Skala im Hinterkopf. In unserem Beispieldatensatz reichen die Bewertungen von 1 bis 5. 1 ist wenig, 5 ist viel. Die Lebenszufriedenheit (m=3.00, sd=1.15) hat den geringsten Durchschnittswert, während die Variable Einkommen (m=3.05, sd=1.14) nur von der Variable Bildung (m=3,07, sd = 1.14) leicht übertroffen wird
Inter-Item-Korrelationsmatrix
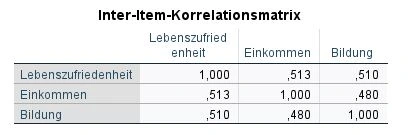
Diese Tabelle zeigt uns die Korrelationen zwischen den einzelnen Items. Wir achten darauf, dass keine Items eine zu hohe KorrelationKorrelation Korrelation bezieht sich auf den Zusammenhang oder die Beziehung zwischen zwei oder mehr Variablen, die durch den Grad der Änderung der Werte einer Variablen im Verhältnis zur Änderung der Werte einer anderen Variablen gemessen wird. aufweisen. Wenn zwei oder mehr Items eine zu hohe Korrelation haben, ist das ein Indikator für Multikolinearität. Das heißt, dass beide Items zu ähnlich sind und im Grunde fast die gleiche Information in sich tragen. Kein Wert sollte eine Korrelation r=.7 oder höher aufweisen! Falls das der Fall ist, sollte das entsprechende Item gegebenenfalls ausgeschlossen werden. In unserem Beispiel fällt die Korrelation zwischen „Lebenszufriedenheit“ und „Einkommen“ mit der Korrelation von r=.51 auf. Die Korrelation ist hoch, aber noch im Rahmen. Das gilt ebenfalls für die anderen Korrelationen.
Item-Skala-Statistiken
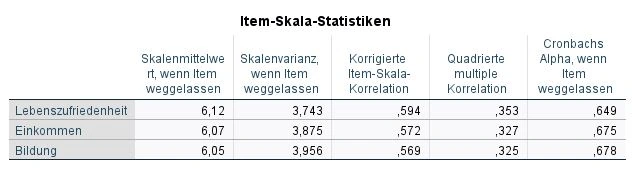
Diese Tabelle gibt uns mehrere Spalten. Zunächst betrachten wir die korrigierte Item-Skala-Korrelation (Corrected Item-Total Correlation). Diese Spalte wird auch als Trennschärfe bezeichnet und sagt uns, wie hoch die einzelnen Items mit den anderen korrelieren. Wir achten darauf, dass kein Wert unter .3 zu sehen ist. In unserem Beispiel wird diese Bedingung problemlos von allen Items erfüllt. In der Regel gilt, dass alle Items mit einer zu geringen Korrelation besser verworfen werden sollten. So können wir den Cronbachs Alpha Wert eventuell erhöhen.
Die letzte Spalte ist für uns sehr insteressiert. Sie sagt aus, wie hoch die Cronabachs Alpha Wert wäre, wenn wir dieses Item nicht in die Berechnung einfließen lassen. Unsere Motivation sollte es sein, die Reliabilität möglichst hochzuhalten, aber nicht zu jedem Preis. Elementare Items sollten nicht ohne weiteres aus der Berechnung ausgeschlossen werden.
In unserem Beispiel bringt der Ausschluss einer Variable keinen Vorteil.
Hinweis: Falls sich durch einen Ausschluss einer Variable der Wert nur unwesentlich ändert, sollte das Item eher bleiben und nicht entfernt werden.
Was mache ich, wenn ich tatsächlich eine Variable ausschließen will?
Ganz einfach. Du startest die Berechnung erneut und lässt bei den Einstellungen die entsprechende Variable einfach aus. Das bedeute, du ziehst die Variable nicht auf das Feld Items.
Wir bleiben in der Tabelle und betrachten die Spalte quadrierte multiple Korrelation (Squared Multiple Correlation) und gibt uns die aufklärenden Varianz (R²), das wir von der Regressionsanalyse kennen. SPSS nimmt uns viel Arbeit ab und berechnet für jedes Item eine eigene multiple Regression, bei der die anderen Variablen als Prädiktoren dienen und übernimmt dabei die Schwächen der Regressionsanalyse: je mehr Items, desto höher fällt R² aus.
Ergebnisse publizieren
Bei der Berechnung der internen Konsistenz wurde ein positiver Cronbach´s Alpha Wert von .751 errechnet. Das ist ein Indikator für eine akzeptable interne Konsistenz.
Fazit zur Reliabilitätsanalyse in SPSS
Insgesamt ist die Reliabilität ein wichtiges Konzept in der Statistik, das die Stabilität oder Zuverlässigkeit von Messwerten beschreibt. Eine Reliabilitätsanalyse kann verwendet werden, um die Reliabilität von Messinstrumenten oder -methoden zu beurteilen und ist besonders wichtig, wenn man Vergleiche zwischen Gruppen oder über Zeit hinweg anstellen möchte.
Es gibt verschiedene Reliabilitätskoeffizienten, die je nach Art der Messung und den verfügbaren Daten geeignet sind, und es ist wichtig, die Stärken und Schwächen der verschiedenen Koeffizienten zu berücksichtigen, wenn man die Reliabilität beurteilt. Wenn man die Reliabilität sorgfältig und kritisch betrachtet, kann man sicherstellen, dass die Messwerte zuverlässig und valide sind und somit für die Analyse und Interpretation der Daten geeignet sind.
5 Fakten zur Reliabilitätsanalyse in SPSS
- Die Reliabilität bezieht sich auf die Stabilität oder Zuverlässigkeit von Messwerten.
- Ein Messinstrument oder eine Messmethode ist reliabel, wenn es die gleichen Ergebnisse liefern würde, wenn es mehrmals angewendet wird.
- Die Reliabilität ist wichtig, wenn man Vergleiche zwischen Gruppen oder über Zeit hinweg anstellen möchte.
- Es gibt verschiedene Reliabilitätskoeffizienten, die je nach Art der Messung und den verfügbaren Daten geeignet sind.
- Die Stärken und Schwächen der verschiedenen Reliabilitätskoeffizienten sollten sorgfältig berücksichtigt werden, wenn man die Reliabilität von Messungen beurteilt.
Reliabilität Testverfahren
| Art der Reliabilität | Testverfahren |
|---|---|
| Interrate Reliabilität | Cohens Kappa |
| Interne Konsistenz | Cohens Alpha |
| Vergleich von Testverfahren | Cohens Kappa |
| Retest-Reliabilität | ◊ Paralleltest-Reliabilität ◊ Split-Half-Reliabilität oder Testhalbierungsmethode ◊ Interne Konsistenz |
Häufig gestellte Fragen und Antworten: Reliabilitätsanalyse in SPSS
Was ist die Reliabilitätsanalyse?
Die Reliabilitätsanalyse ist ein statistisches Verfahren, das verwendet wird, um die Zuverlässigkeit oder Stabilität von Messungen oder Tests zu bewerten. Eine Messung oder ein Test ist dann zuverlässig, wenn sie die gleichen Ergebnisse liefert, wenn sie mehrmals durchgeführt wird.
Test-Retest-Reliabilität: Diese Art von Reliabilität wird verwendet, um die Stabilität von Messungen oder Tests über einen längeren Zeitraum hinweg zu bewerten. Zum Beispiel könnte man die Test-Retest-Reliabilität eines Persönlichkeitstests untersuchen, indem man den Test zu zwei verschiedenen Zeitpunkten bei den gleichen Personen durchführt und dann vergleicht, wie ähnlich die Ergebnisse sind.
Inter-Rater-Reliabilität: Diese Art von Reliabilität wird verwendet, um die Übereinstimmung zwischen zwei oder mehr Beurteilern zu bewerten, die dieselben Messungen oder Tests durchführen. Zum Beispiel könnte man die Inter-Rater-Reliabilität von Schulleistungsbewertungen untersuchen, indem man zwei oder mehr Lehrer beauftragt, dieselben Schüler zu bewerten und dann vergleicht, wie ähnlich ihre Bewertungen sind.
Parallele Formen-Reliabilität: Diese Art von Reliabilität wird verwendet, um die Stabilität von Messungen oder Tests über einen längeren Zeitraum hinweg zu bewerten. Sie wird verwendet, wenn es zwei oder mehr ähnliche Versionen eines Tests oder einer Messung gibt, die man als parallele Formen bezeichnet. Die Parallele Formen-Reliabilität ist besonders nützlich, wenn man Tests oder Messungen verwendet, die über einen längeren Zeitraum hinweg durchgeführt werden, zum Beispiel in der Bildung oder in der psychologischen Diagnostik.
Was sagt Cronbach Alpha aus?
Cronbach Alpha ist ein Maß für die interne Konsistenz oder Reliabilität von Messungen oder Tests. Es wird verwendet, um zu bewerten, wie gut die Fragen oder Items, die in einem Test enthalten sind, zusammenarbeiten, um eine bestimmte Konstruktion oder ein Konzept zu messen.
Cronbach Alpha wird auf einer Skala von 0 bis 1 berechnet, wobei ein höherer Wert für eine höhere interne Konsistenz oder Reliabilität steht. Ein Cronbach Alpha-Wert von 0,7 oder höher wird allgemein als akzeptabel betrachtet, während ein Wert von 0,8 oder höher als sehr gut betrachtet wird.
Cronbach Alpha ist besonders nützlich, wenn man Tests oder Messungen verwendet, die aus mehreren Fragen oder Items bestehen, zum Beispiel in der Bildung oder in der psychologischen Diagnostik.
Wann Cronbachs Alpha verwenden?
Cronbach Alpha kann verwendet werden, um zu beurteilen, ob ein Test oder eine Messung zuverlässig genug ist, um als Grundlage für wichtige Entscheidungen zu dienen, zum Beispiel in der personalpsychologischen Auswahl oder bei der Diagnose von psychischen Störungen.
Es ist jedoch wichtig zu beachten, dass Cronbach Alpha nur ein Maß für die interne Konsistenz ist und keine Aussage darüber macht, ob der Test oder die Messung valide ist, d.h. ob sie tatsächlich das misst, was sie vorgibt zu messen. Validität ist eine separate Eigenschaft, die auf andere Weise untersucht werden muss.
Was tun bei schlechtem Cronbachs Alpha?
Wenn die Cronbach Alpha-Werte eines Tests oder einer Messung unter dem akzeptablen Niveau von 0,7 liegen, könnten einige Schritte unternommen werden, um die interne Konsistenz oder Reliabilität zu verbessern:
– Überprüfung der Fragen oder Items: Es könnte hilfreich sein, die Fragen oder Items im Test oder in der Messung zu überprüfen, um sicherzustellen, dass sie alle zu einem einheitlichen Konzept oder einer einheitlichen Konstruktion beitragen. Es könnte auch nützlich sein, die Fragen oder Items auf Verständlichkeit und Fehlerfreiheit zu überprüfen.
– Entfernen von Fragen oder Items: Es könnte sinnvoll sein, Fragen oder Items aus dem Test oder der Messung zu entfernen, die nicht gut zu den anderen Fragen oder Items passen oder die die interne Konsistenz verringern.
– Verbesserung der Instruktionen und der Verwaltung: Es könnte nützlich sein, die Instruktionen für den Test oder die Messung zu überarbeiten, um sicherzustellen, dass sie klar und verständlich sind, und die Verwaltung des Tests oder der Messung zu verbessern, um sicherzustellen, dass sie konsistent durchgeführt wird.
Es ist jedoch wichtig zu beachten, dass eine Verbesserung der interne Konsistenz oder Reliabilität des Tests oder der Messung nicht automatisch bedeutet, dass sie auch valide ist, d.h. dass sie tatsächlich das misst, was sie vorgibt zu messen. Validität ist eine separate Eigenschaft, die auf andere Weise untersucht werden muss.
Was sind weiterführende Links zu Reliabilität prüfen in SPSS
Was beeinflusst Reliabilität?
Die Reliabilität von Messungen oder Tests kann von verschiedenen Faktoren beeinflusst werden. Hier sind einige Beispiele:
– Qualität der Fragen oder Items: De Qualität der Fragen oder Items, die in einem Test oder einer Messung enthalten sind, kann die Reliabilität beeinflussen. Fragen oder Items, die unklar, fehlerhaft oder nicht zu einem einheitlichen Konzept oder einer einheitlichen Konstruktion beitragen, können die Reliabilität verringern.
– Instruktionen und Verwaltung: Die Qualität der Instruktionen und der Verwaltung des Tests oder der Messung kann die Reliabilität beeinflussen. Wenn die Instruktionen unklar sind oder wenn der Test oder die Messung nicht konsistent durchgeführt wird, kann dies die Reliabilität verringern.
– Testbedingungen: Die Testbedingungen können die Reliabilität beeinflussen. Zum Beispiel könnten Ablenkungen oder Störfaktoren während des Tests die Reliabilität verringern.
– Population: Die Zusammensetzung der Population, für die der Test oder die Messung entwickelt wurde, kann die Reliabilität beeinflussen. Wenn der Test oder die Messung nicht für die Population, für die er verwendet wird, validiert wurde, kann dies die Reliabilität verringern.
Es ist wichtig zu beachten, dass die Reliabilität nur eine Eigenschaft von Messungen oder Tests ist und keine Aussage darüber macht, ob sie valide sind, d.h. ob sie tatsächlich das messen, was sie vorgibt zu messen. Validität ist eine separate Eigenschaft, die auf andere Weise untersucht werden muss.

Über mich: Dr. Peter Merdian
Experte für Neuromarketing und Data Science
Hallo, mein Name ist Peter Merdian und Statistic Hero ist mein Herzensprojekt, um Menschen zu helfen, einen einfachen Einstieg in die Statistik zu finden. Ich hoffe, die Anleitungen gefallen dir und du findest nützliche Informationen! Ich habe selbst in Neuromarketing promoviert und liebe datengetriebene Analysen. Besonders mit komplexen Zahlen. Ich kenne aus eigener Erfahrung alle Probleme, die man als Studierender während des Studiums hat. Deshalb sind die Anleitungen so praxisnah und einfach wie möglich gehalten. Fühl dich frei, die Anleitungen mit deinen eigenen Datensätzen auszuprobieren und spannende Ergebnisse zu berechnen. Ich wünsche dir viel Erfolg bei deinem Studium, deiner Forschung oder deiner Arbeit.
Möchtest du mir Feedback geben oder mich kontaktieren?
Bitte hier: Dr. Peter Merdian LInkedIn